2.1.3 Расчет рабочих поверхностей зубьев колес на статическую прочность по контактным напряжениям

При действии на зубья кратковременных перегрузок требуется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

, где

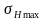– максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ;

– допускаемое максимальное напряжение для зубьев, Па;

– расчетное контактное напряжение.

Для зубьев зубчатых колес с термообработкой нормализацией, улучшением или объемной закалкой с отпуском , где – предел текучести материала зубьев при растяжении;

из технического задания равняется 900 МПа.

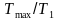– кратность моментов электродвигателя, где – пусковой момент, – номинальный момент.

Согласно таблице 24.9 [1, c.459] = 2,2;

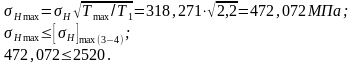
Расчеты показали, что назначенные размеры зубчатой передачи удовлетворяют условиям статической прочности.

2.1.4 Проверочный расчет на сопротивление усталости зубьев колес по напряжениям изгиба

Согласно 12.69 [2, c.188]:

Согласно [2, c.189]: 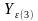=1;

Согласно [2, c.190]: ;

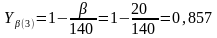Согласно 12.23 [2, c.189]: = 4,1;

;

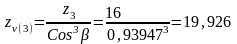Согласно 12.17б [2, c.181]: 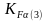=1,19;

Согласно 12.18 [2, c.183]: 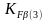=1,29;

Согласно табл.12.5 [2, c.191]: =1,03;

Согласно [2, c.195]: ;

Согласно CT CЭВ 229 – 75 [2, c.195]: 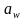=100мм для нашего случая;

Принимаем значение = 1,175 смотри пункт 2.1.1.3.

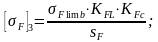
Согласно [2, c.191]: = 1,7;

Согласно таблице 12.6 [2, c.192]: 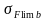= 750;

Согласно 12.74 [2, c.191]: 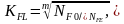где

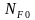– базовое число циклов напряжений, согласно [2, c.191]:

4*10⁶;

– эквивалентное число циклов напряжений.

Согласно 12.75 [2, c.191]:

– число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом.

Согласно [2, c.191]: = 1;

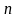– частота вращения рассчитываемого зубчатого колеса.

Согласно пункту 1.3 об/мин;

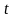– продолжительность работы передачи под нагрузкой за расчетный срок службы;

Согласно пункту 2.1.1.3 =24.528 час.

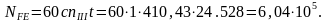
Теперь найдем :

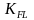1,234.

Согласно [2, c.190]: 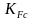= 1;

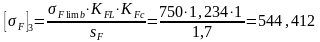
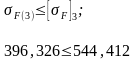
Расчеты показали, что проверочный расчет на сопротивление усталости зубьев колес по напряжениям изгиба удовлетворяет условию прочности.

2.1.5 Расчет зубчатых передач по программе zub

При расчете передачи 3 – 4 по программе ZUB были получены следующие данные: межосевое расстояние a_w3-4 = 85 мм; передаточное число u_3-4 = 5,37; крутящий момент T_IV = 218,8 Н*м; числа зубьев шестерни и колеса 18 и 99 соответственно; начальный диаметр шестерни d_w3 = 27,69; начальный диаметр колеса d_w4 = 152,31 мм.

При повторном прогоне программы при попытке уменьшить межосевое расстояние до 80 мм, значение крутящего момента T_IV стало меньше и данные результаты не удовлетворяют заданному условию.

Таким образом, результаты, полученные при первом прогоне программы, берем за проектные.

При использовании программы ZUB при расчете передачи 1 – 2 были получены следующие результаты, а именно: передаточное число u_1-2 = 9,94; межосевое расстояние a_w1-2 = 67 мм; крутящий момент Т_III = 40,5 Н*м.

При повторном прогоне программы при попытке уменьшить a_w1-2 до 60 мм крутящий момент Т_III получился меньше заданного, следовательно расчеты при межосевом расстоянии равным 67 мм удовлетворяют заданным условиям.

Как в случае передачи 3 – 4, результаты, полученные при использовании программы ZUB для передачи 1 – 2, берем за проектные.

Более подробные значения для передач смотри в бланке программы ZUB, приложение 2.

Расхождения результатов, полученных методическим расчетом, с результатами, полученных при использовании программы ZUB, объясняется тем, что в программе значения коэффициентов были взяты более точно, а так же тем, что согласно техническому заданию необходимо было округлять значения межосевых расстояний до целых, кратных 0 и 5.