2. Построение положений механизма.

Для построения кинематической схемы исследуемого механизма в различных положениях выбираем масштабный коэффициент длины , который определяется как

= [ ]

где - действительный радиус кривошипа в м;

АВ – радиус кривошипа на чертеже в мм.

Масштабный коэффициент _l следует выбрать таким образом, чтобы схема механизма занимала примерно 1/5 часть листа и чтобы этот коэффициент был удобен для расчетов. Например могут быть использованы следующие значения :

0,001 м/мм; 0,0005 м/мм; 0,002 м/мм; 0,0025 м/мм.

Все требуемые положения механизма удобно строить на одном чертеже (т.е. с одним центром вращения кривошипа). На рис. 20 механизм показан в четырех положениях. Каждое положение обозначено соответствующим индексом:

1 – соответствует верхнему крайнему положению ползуна 5 (ведомого

звена),

П – соответствует нижнему крайнему положению ползуна 5,

Ш – соответствует рабочему ходу ползуна 5 ,

1У – соответствует холостому ходу ползуна 5.

Крайние положения исследуемого рычажного механизма с качающейся кулисой определяем по крайним положениям кулисы 3 , в которых кулиса перпендикулярна кривошипу 1 .

Рабочему ходу ползуна соответствует угол поворота кривошипа _{р.х. ,} холостому ходу - _х.х.

При выборе расчетного рабочего положения используем диаграмму сил F = F(S_е), построенную на ходе ползуна 5 . В металлорежущих станках процесс резания происходит только на части рабочего хода, соответствующей длине обрабатываемой детали . Поэтому выбираем положение кривошипа на угле поворота _{р.х. ,} соответствующем рабочему ходу, когда ползун 5 (точка Е ) внутри отрезка .

При выборе положения механизма, соответствующего холостому ходу ползуна, берем любое положение кривошипа на угле его поворота _х.х.

6.3. Построение планов скоростей и ускорений.

Планы скоростей и ускорений требуется построить для трех положений механизма: для положений на рабочем и холостом ходах и для одного из крайних положений. Рассмотрим построение плана скоростей и ускорений для рабочего положения механизма.

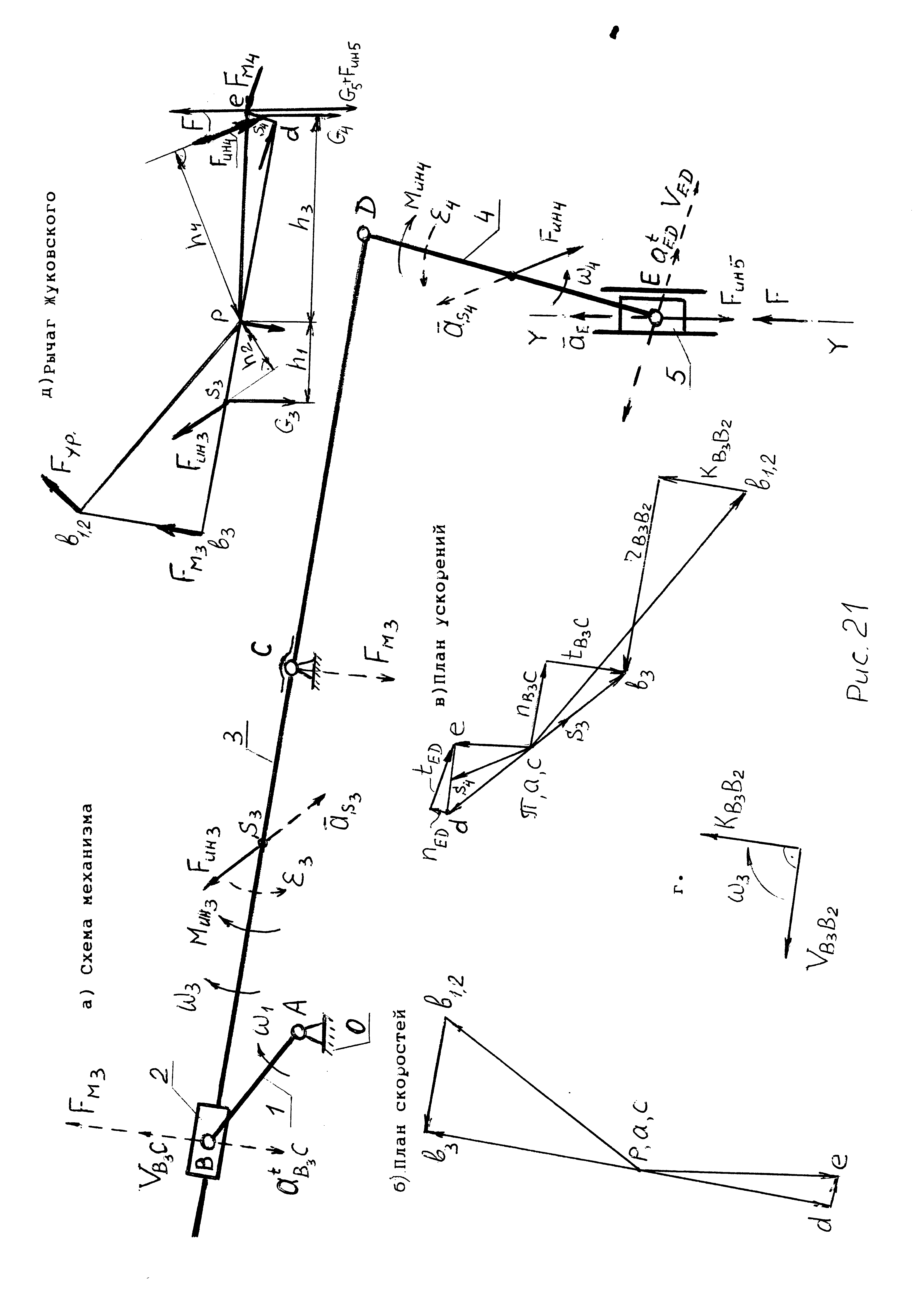
На рис 21,а (чтобы лучше были видны построения) вынесено отдельное положение, соответствующее рабочему ходу.

Последовательность кинематического исследования определена последовательностью образования механизма: начальное звено 1 и стойка 0

двухповодковая группа Ассура 3 вида, состоящая из звеньев 2 и 3 ,  двухповодковая группа Ассура 2 вида, состоящая из звеньев 4 и 5 .

Для начального звена 1 угловая скорость постоянна и равна ₁ = [с^-1 ], где n [мин^-1] – заданная частота вращения кривошипа.

Скорость точки В₁ начального звена равна

,

вектор скорости направлен перпендикулярно звену АВ в сторону, соответствующую направлению угловой скорости .

На плане скоростей (рис. 21, б) скорость точки В₁ изображаем отрезком . Масштабный коэффициент плана скоростей

.

На листе проекта отрезок рекомендуется принять порядка 50…70 мм, но так, чтобы был удобным для расчетов. Например, если м/с, то удобно взять равным 76 мм, тогда

, т.к. звенья 1 и 2 связаны вращательной кинематической парой, а , т.к. звенья 2 и 3 связаны поступательной кинематической парой. Для точки В₃ согласно II-ому способу разложения движения (§3):

_ _ _

,

где . Поэтому через точку в_1,2 проводим прямую, параллельную ВС. Согласно первому способу разложения движения:

_ _ _

,

где . Поэтому через точку с проводим прямую, перпендикулярную ВС.

Точка пересечения этих прямых и есть точка (стрелки ставим к этой точке).

На схеме механизма точка D лежит на продолжении отрезка ВС звена 3. Следовательно и на плане скоростей точка d будет лежать на продолжении отрезка в соответствии с теоремой о подобии. Отрезок dc определяем из пропорции

или т.к. точка С на плане совпадает с полюсом р.

Далее переходим ко второй группе Ассура, включающей звенья 4 и 5. Для точки Е, согласно I-ому способу разложения движения

,

где V_E // xx, т.к. точка Е вместе с пятым звеном движется поступательно по горизонтали, а V_ED ED. Поэтому через полюс р проводим прямую параллельную х-х, т.к. все абсолютные скорости выходят из полюса, а через точку d проводим прямую, перпендикулярную ED. Точка пересечения этих прямых есть точка е (стрелки ставим к этой точке).

Пользуясь построенным планом скоростей, можно определить угловые скорости звеньев:

,

.

_

Для определения направления переносим вектор скорости в точку В на схеме механизма и рассматриваем движение точки В относительно

точки С в направлении скорости . В данном положении механизма угловая скорость направлена по часовой стрелке. Для определения направления переносим вектор относительной скорости в точку Е и рассматриваем движение точки Е относительно точки D. В данном положении механизма направлена против часовой стрелки.

Переходим к построению плана ускорений. Ускорение точки В₁ равно нормальному ускорению при вращении точки В вокруг точки А , т.к. и направлено к центру вращения (от В к А):

.

На плане ускорений (рис. 21, в) выбираем отрезок порядка 50…70 мм из условия, чтобы масштабный коэффициент плана ускорений получился величиной, удобной для расчета:

.

Векторные равенства для нахождения ускорения точки В₃ имеют вид:

_ _ _ _

_ _ _ _

.

^{от В к С}

Кориолисово ускорение, вернее отрезок, изображающий его на плане ускорений, определяем по формуле:

,

где и - отрезки с плана скоростей, (ВС) – отрезок со схемы механизма,

.

Чтобы определить направление , нужно отрезок , изображающий скорость , повернуть в сторону на 90⁰ (рис. 21, г).

Нормальное ускорение при вращении точки В₃ относительно точки С направлено по звену ВС от точки В к точке С, а отрезок, его изображающий, равен

.

Графическое решение векторных равенств показано на рис. 21в.

Ускорение точки D кулисы 3 определяем согласно теореме о подобии пропорциональным делением одноименных отрезков на схеме механизма и на плане ускорений.

; .

Далее записываем векторное равенство для следующей 2ПГ 2-го вида, включающей звенья 4 и 5:

_ _ _ _

^{// уу от Е к D ED}

Отрезок , изображающий на плане ускорений нормальное ускорение при вращении точки Е вокруг точки D, равен

.

Необходимые построения показаны на рис. 21,в.

Пользуясь построенным планом ускорений, определим угловые ускорения звеньев:

;

.

Для определения направления углового ускорения звена 3 переносим с плана ускорений вектор тангенциального ускорения , (направленный отрезок ) в точку В механизма. Угловое ускорение направлено против часовой стрелки.

Для определения направления углового ускорения звена 4 переносим с плана ускорений вектор тангенциального ускорения в точку Е механизма (вращение относительно точки D). Угловое ускорение направлено против часовой стрелки (рис. 21, а).

Аналогично должны быть построены планы скоростей и ускорений для положений IV и I (или II). При этом используются те же векторные равенства и желательно использовать те же масштабные коэффициенты Результаты повторяющихся расчетов могут быть приведены в записке в виде следующей таблицы:

Номер положения
III (p.x.) IV (x.x.) I (к.п.)

При построении планов скоростей и ускорений для крайнего положения механизма можно руководствоваться примерами, приведенными в разделе 3.