4. Кинетостатический расчет механизма.

4.1. Определение сил инерции звеньев.

В общем случае плоско-параллельного движения звена силы инерции всех элементарных масс звена могут быть приведены к одной силе инерции, приложенной в центре масс звена, и к паре сил инерции.

Сила инерции определяется как произведение массы звена на ускорение центра масс

F_и = - m а _S

Направлена сила инерции в сторону, противоположную ускорению центра масс и приложена в центре масс звена.

Момент пары сил инерции (момент сил инерции звена) равен произведению момента инерции относительно оси, проходящей через центр масс, на угловое ускорение звена:

M_и = - I_S 

Направление действия момента противоположно угловому ускорению звена.

Ускорения центров масс звеньев определяют по плану ускорений, пользуясь теоремой о подобии. Угловое ускорение каждого звена определяется как частное от деления относительного тангенциального ускорения каких-либо двух точек этого звена на расстояние между этими точками на механизме.

4.2. Определение реакций в кинематических парах и уравновешивающей силы на кривошипе.

Все силы, действующие на механизм (веса звеньев, силы инерции, моменты сил инерции, внешняя сила F , определенная по диаграмме сил для рассматриваемого положения механизма) наносим на схему механизма в соответствующие точки и определяем реакции в кинематических парах и F_ур.

Реакции определяются отдельно для каждой группы Ассура, начиная с последней присоединенной группы, так как порядок кинетостатического расчета обратен порядку присоединения групп Ассура к начальному звену и стойке.

При выделении групп Ассура из механизма действие отброшенных звеньев заменяем действием реакций, которые необходимо определить. Кроме того, в каждой группе Ассура есть внутренняя кинематическая пара, реакция на элементах которой также неизвестна. Реакцию в кинематической паре обозначаем двумя цифрами, соответствующими номерам звеньев, образующих кинематическую пару. При этом первая цифра – номер звена, на которое действует сила, а вторая цифра - номер звена, со стороны которого действует сила. Например, реакция F₁₂ – это сила, с которой на звено 1 действует звено 2 . Согласно третьему закону Ньютона F₁₂ = -F₂₁ ( F₂₁ - сила, с которой на звено 2 действует звено 1 ).

Рассмотрим определение неизвестных реакций в кинематических парах двухповодковых групп Ассура всех разновидностей. Звенья группы Ассура обозначим номерами 2 и 3 . Все внешние силы и моменты, действующие на звенья группы Ассура, а также силы инерции и моменты сил инерции, считаем известными. Для каждого звена представим их результирующими силами и моментами - F₂, F₃, М₂, М_3. Пунктиром обозначим звенья 1 и 4 , к которым выделенная группа Ассура присоединена в механизме. Подлежат определению три вектора: F₂₁, F₃₄, F₂₃ = F₃₂.

 При наличии в группе звена, входящего в две вращательные пары. или двух внешних вращательных пар (двухповодковые группы Ассура 1, 2 и 3 видов) неизвестную реакцию во внешней вращательной паре разложим на две

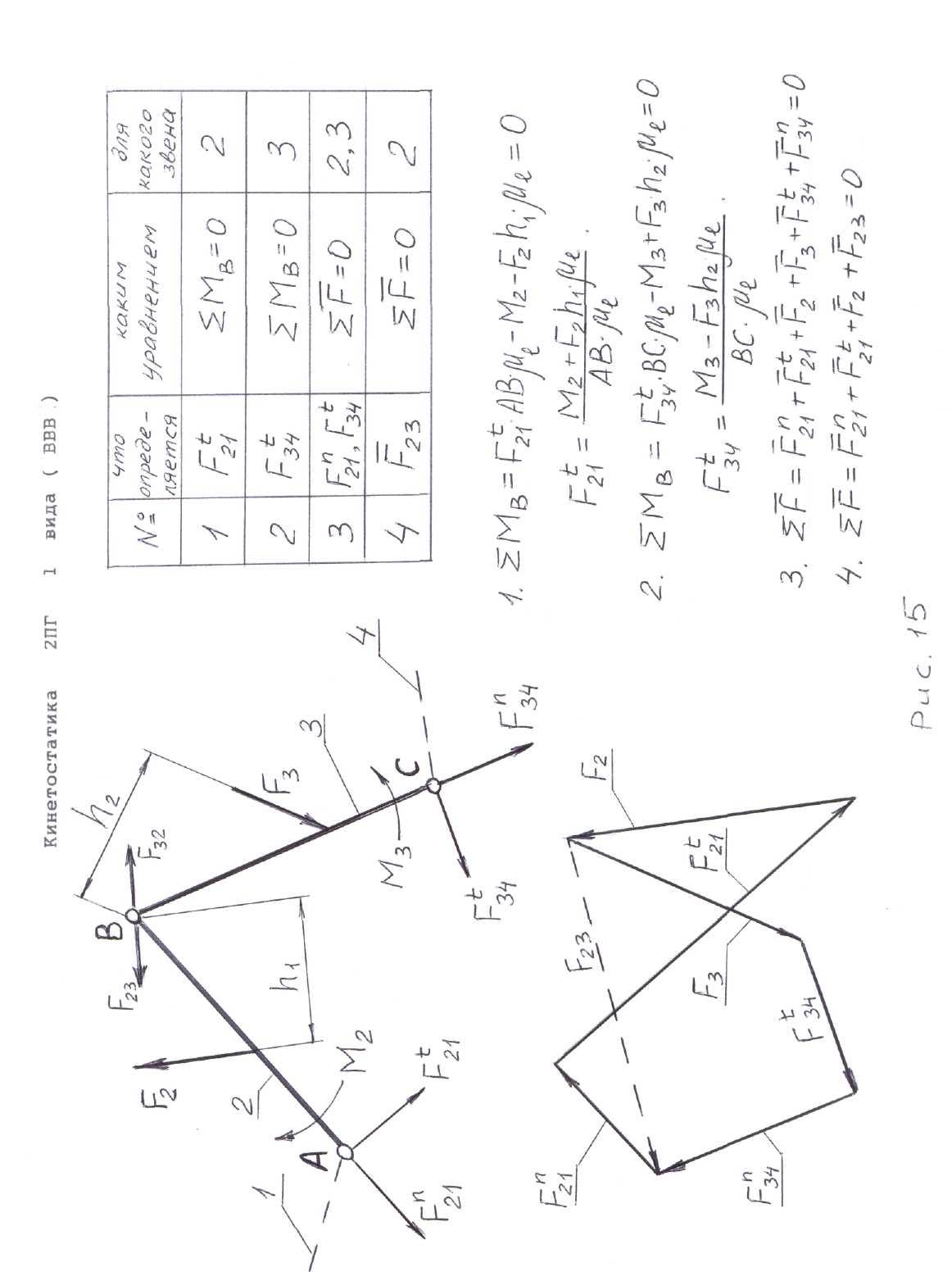
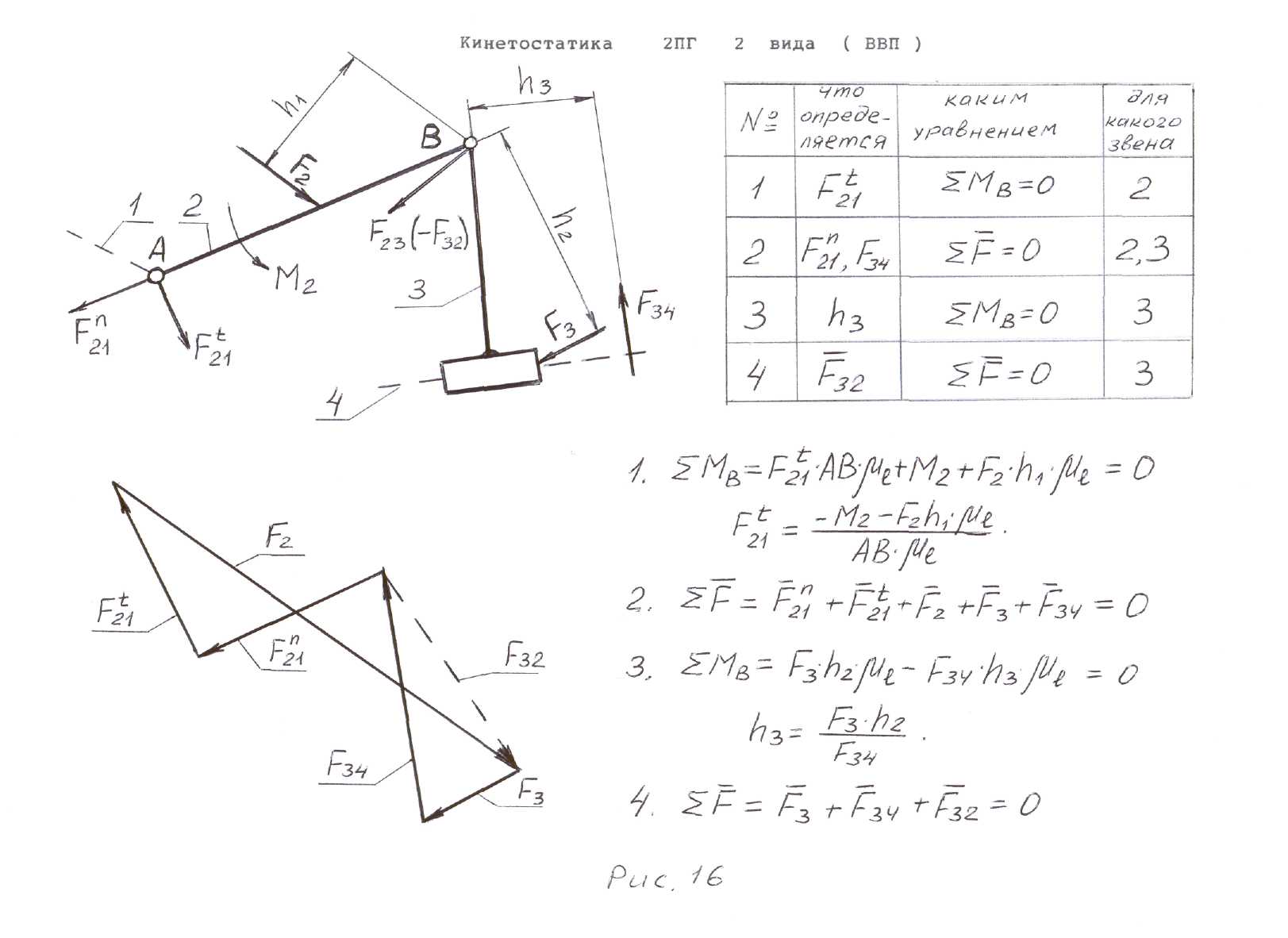
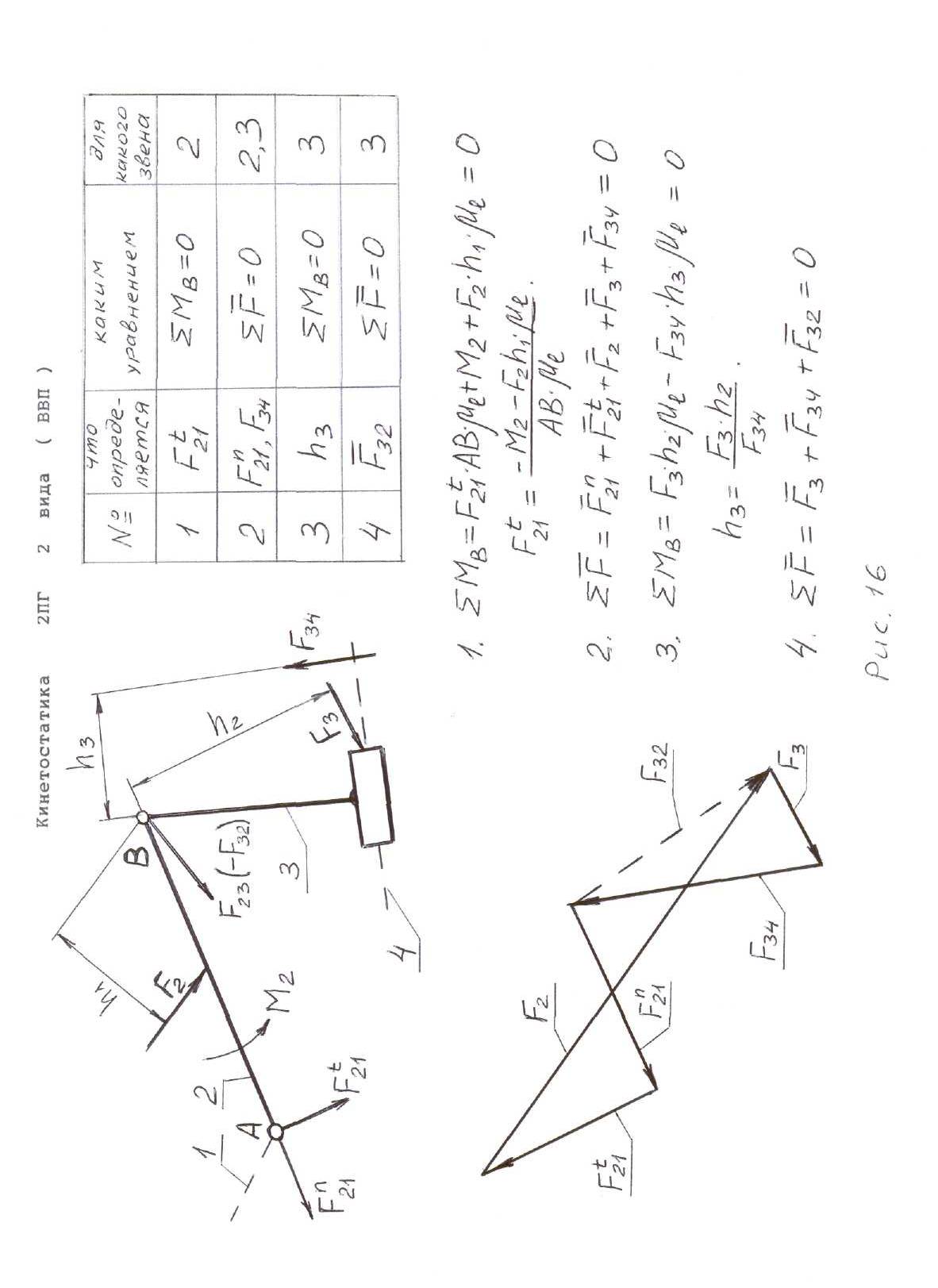
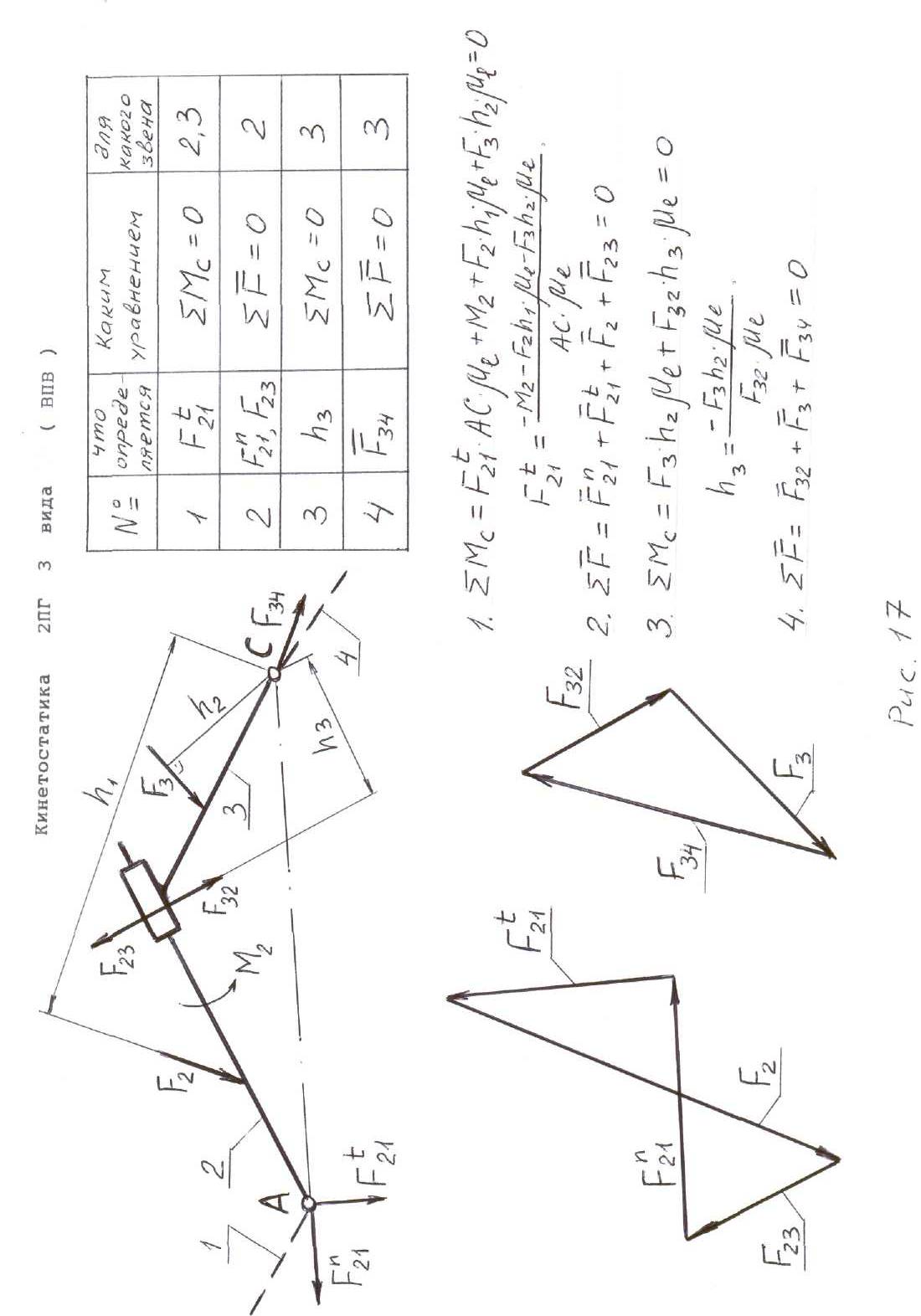
составляющие: нормальную Fⁿ , действующую вдоль звена и тангенциальную F^t перпендикулярно звену.

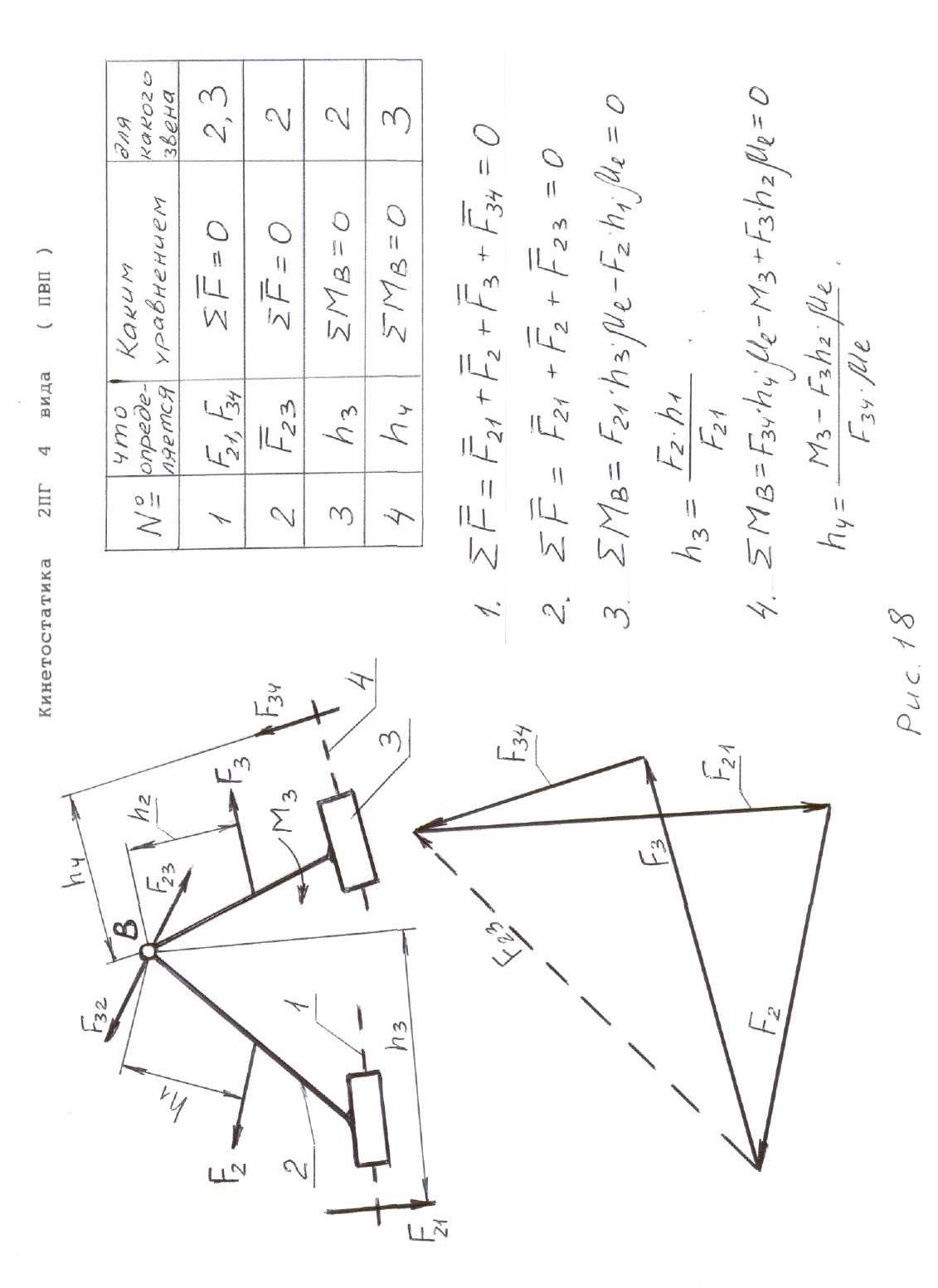
Последовательность кинетостатического расчета двухповодковых групп Ассура пяти видов, необходимые уравнения для определения неизвестных реакций, а также силовые многоугольники приведены на рис. 15, 16, 17, 18, 19.

Определив последовательно реакции в кинематических парах всех групп Ассура, переходим к начальному звену и определяем уравновешивающую силу.

Пример определения сил инерции, реакций в кинематических парах и уравновешивающей силы подробно разобран в разделе 6.4.