3. Построение планов скоростей и ускорений.

Кинематическое исследование механизма методом построения планов скоростей и ускорений ведется по группам Ассура в порядке присоединения их к начальному звену и стойке. Для любой двухповодковой группы Ассура известны (или могут быть определены по теореме о подобии) скорости, ускорения внешних кинематических пар и совместным решением двух векторных уравнений можно определить скорость, ускорение внутренней кинематической пары. При составлении векторных уравнений используются два способа разложения движения:

1 способ применяется, когда известно движение одной точки звена (например, точки В) и требуется определить движение другой точки того же звена (точки С). При этом движение звена раскладывается на переносное поступательное со скоростью и ускорением первой точки (точки В) и на относительное вращательное вокруг этой точки.

2 способ применяется, когда известно движение точки одного звена (точки В₁) и требуется определить движение точки второго звена (точки В₂), и эти два звена образуют поступательную кинематическую пару. При этом движение второго звена раскладывается на переносное движение второго вместе с первым звеном и на относительное поступательное движение второго звена вдоль направляющей первого звена .

Теорема о подобии применяется для точек одного звена, когда известны скорости, ускорения двух точек одного звена и требуется определить скорость и ускорение третьей точки того же звена:

относительные скорости и ускорения точек одного звена образуют на планах скоростей и ускорений фигуры, подобные фигурам, которые одноименные точки образуют на схеме механизма. Эти фигуры сходственно расположены, т.е. при чтении буквенных обозначений их вершин в одинаковом направлении буквы следуют в одинаковом порядке.

В качестве примера применения двух способов разложения движения и теоремы о подобии рассмотрим построение планов скоростей и ускорений для некоторых простейших механизмов.

Пример 1. Построить план скоростей и ускорений для заданного положения кривошипно-ползунного механизма (рис. 7). Известны размеры звеньев и и угловая скорость _{1 =} const начального звена 1 .

Для начального звена определяем величину скорости точки В:

Вектор V_В перпендикулярен радиусу АВ и направлен в сторону, соответствующую направлению _1. Для изображения скорости точки В на плане скоростей выбираем произвольный по величине отрезок рв (АВ) (рис. 8). Тогда масштабный коэффициент плана скоростей определится как

_V =

Для определения скорости точки С раскладываем движение звена 2 (первый способ разложения движения) на переносное поступательное со скоростью точки В и на относительное вращательное точки С вокруг точки В.

_ _ _

где V_C  ХХ, т.к. ползун перемещается в неподвижных направляющих и поэтому абсолютные скорость и ускорение любой его точки параллельны оси направляющих XX , а V_CB  СВ, как скорость в относительном вращательном движении. Согласно этому векторному равенству проводим построение на плане скоростей. Через полюс (откуда выходят все абсолютные скорости) проводим прямую параллельную XX , а через точку в – прямую перпендикулярную BC. Точка пересечения этих прямых определяет искомую точку с. Отрезок pс плана скоростей изображает в выбранном масштабе скорость точки C: V_C = _V (pc). Как видно из чертежа, вектору относительной скорости V_CB на плане скоростей соответствует отрезок вс со стрелкой, направленной к точке C т.е. буквенное обозначение вектора относительной скорости на плане скоростей следует читать в порядке, обратном по сравнению с порядком букв в индексе соответствующей скорости. Величина относительной скорости V_CB = (вc) _V.

В приведенном выше равенстве (для V_C ), как и в следующих равенствах, двумя чертами подчеркнуты векторы, известные по величине и направлению, а одной чертой – векторы, известные либо только по величине, либо только по направлению.

Пользуясь построенным планом скоростей, определим угловую скорость звена 2:

₂ = [с^-1]

Для определения направления ₂ переносим вектор скорости V_CB в точку C механизма и рассматриваем движение точки C относительно точки B в направлении скорости V_CB . На рис. 7 показано направление ₂.

Построение плана ускорений начинаем с определения ускорения точки B. Так как угловая скорость кривошипа принята постоянной, то ускорение точки В равно нормальному ускорению, величина которого определяется как

а _B =

Направлено это ускорение по кривошипу AB от точки B к точке A (к центру вращения). Для изображения ускорения точки B на плане ускорений (рис.9) выбираем произвольный отрезок в  AB. Тогда масштабный коэффициент плана ускорений определится отношением

_а = [ ]

Для определения ускорения точки С напишем векторное равенство (первый способ разложения движения)

_ _ _ _

Так как при разложении движения звена 2 за переносное движение принято поступательное (т.е. _пер = 0), то в векторном равенстве отсутствует кориолисово ускорение. Вектор нормального ускорения аⁿ_CB (при вращательном движении относительно точки В ) направлен к центру вращения, т.е.  СВ от С к В , а вектор тангенциального ускорения a^t_CB направлен перпендикулярно нормальному ускорению, т.е. перпендикулярно СВ. Величину нормального ускорения определяем по формуле

аⁿ_CB = [ м/с² ],

а отрезок n _CB , изображающий на плане это ускорение –

n_CB = [мм]

где  = _V² / _l _а

На плане ускорений через точку в проводим прямую, параллельную звену CB в направлении от C к B , и на ней откладываем подсчитанный отрезок n_CB, изображающий аⁿ_CB , а через конец этого направленного отрезка проводим прямую, перпендикулярную BC . Точка C найдется как точка пересечения этой прямой и прямой, проведенной через полюс параллельно XX. Тогда же определится и отрезок t_CB , изображающий ускорения а^t_CВ..

Скорость и ускорение точки D, принадлежащий звену 2, найдем, исходя из теоремы о подобии, так как у этого звена уже известны скорости и ускорения двух точек: В и С . По теореме о подобии относительные скорости и ускорения точек одного и того же звена образуют на планах скоростей и ускорений фигуры, подобные одноименной фигуре на схеме механизма. Следовательно, на планах скоростей и ускорений необходимо построить треугольники вdc (рис.8,9), подобные треугольнику ВDС на механизме (рис.7). Треугольник вdc на плане скоростей и треугольник ВDС на механизме являются треугольниками со взаимноперпендикулярными сторонами. Поэтому для построения искомого треугольника вdc на плане скоростей из точки в проводим прямую, перпендикулярную ВD , а из точки c – прямую перепендикулярную СD . Их пересечение и определит точку d , соединяя которую с полюсом р , получаем абсолютную скорость точки D в масштабе _{V :} V_D = ( pd ) _V .

На плане ускорений рационально строить треугольник вdc следующим образом. Отрезок вc с плана ускорений откладывается на прямой ВС (рис.7) от любой точки В или С . Затем по отрезку вc на механизме строится треугольник подобный треугольнику ВDС, для чего через точку в проводим прямую  ВD. Полученные две стороны этого треугольника (вd ) = r₁ и

(dc ) = r₂ по величине равны сторонам искомого треугольника на плане ускорений, который может быть построен с помощью засечек с соблюдением сходственности расположения фигур, как показано на рис.9.

Абсолютное ускорение точки D : а _D = (d ) _а .

Если требуется найти скорость и ускорение точки Е , принадлежащей звену 2 и расположенной непосредственно на прямой ВС, то вместо построения треугольника требуется лишь произвести пропорциональное деление отрезка вc как на плане скоростей, так и на плане ускорений согласно пропорции . В итоге

V_E = (pe ) _V а_E = (e) _а

Для одного из крайних положений кривошипно-ползунного механизма планы скоростей и ускорений показаны на рис. 10.

Здесь V_C = 0; V_CB = V_B, но векторы противоположно направлены, т.е.

_

V _СB = - V_{B .} При построении находим, что а^t _CB = 0.

Пример 2. Построить план скоростей и ускорений для заданного

положения механизма шарнирного четырехзвенника (рис.11, а), если известны размеры звеньев механизма и ₁ = const .

В этом механизме применяется только первый способ разложения движения звеньев. Векторные равенства для построения скоростей и ускорений точки С и условия их построения удобно привести в следующем виде:

[ ]АВ [ ] от В к А

[ ] [ ]

_{_ _}_ _{__}_ _{_ _} _ _ _{_}_ _{_}_ _ _{_}

+ + +

^{от С к В}

_ _ _ _ _ _ _

+ + +

^{от С к D}

Графическое решение векторных равенств показано для скоростей на рис. 11б, для ускорений - на рис. 11в.

Для крайнего положения механизма план скоростей и ускорений показан на рис. 12. Здесь V_C = 0 и а ⁿ_СD = 0.

Пример 3. Построить план скоростей и ускорений для механизма с качающейся кулисой (рис.13а) при заданной ₁ = const и заданных размерах и .

Скорость точки В₁ , принадлежащей звену 1 , V_B1 = и направлена перпендикулярно АВ. Точка В₂ , принадлежащая звену 2 , имеет такую же скорость, т.к. точка В - это центр шарнира, соединяющего между собой звенья 1 и 2 . Можно написать, что

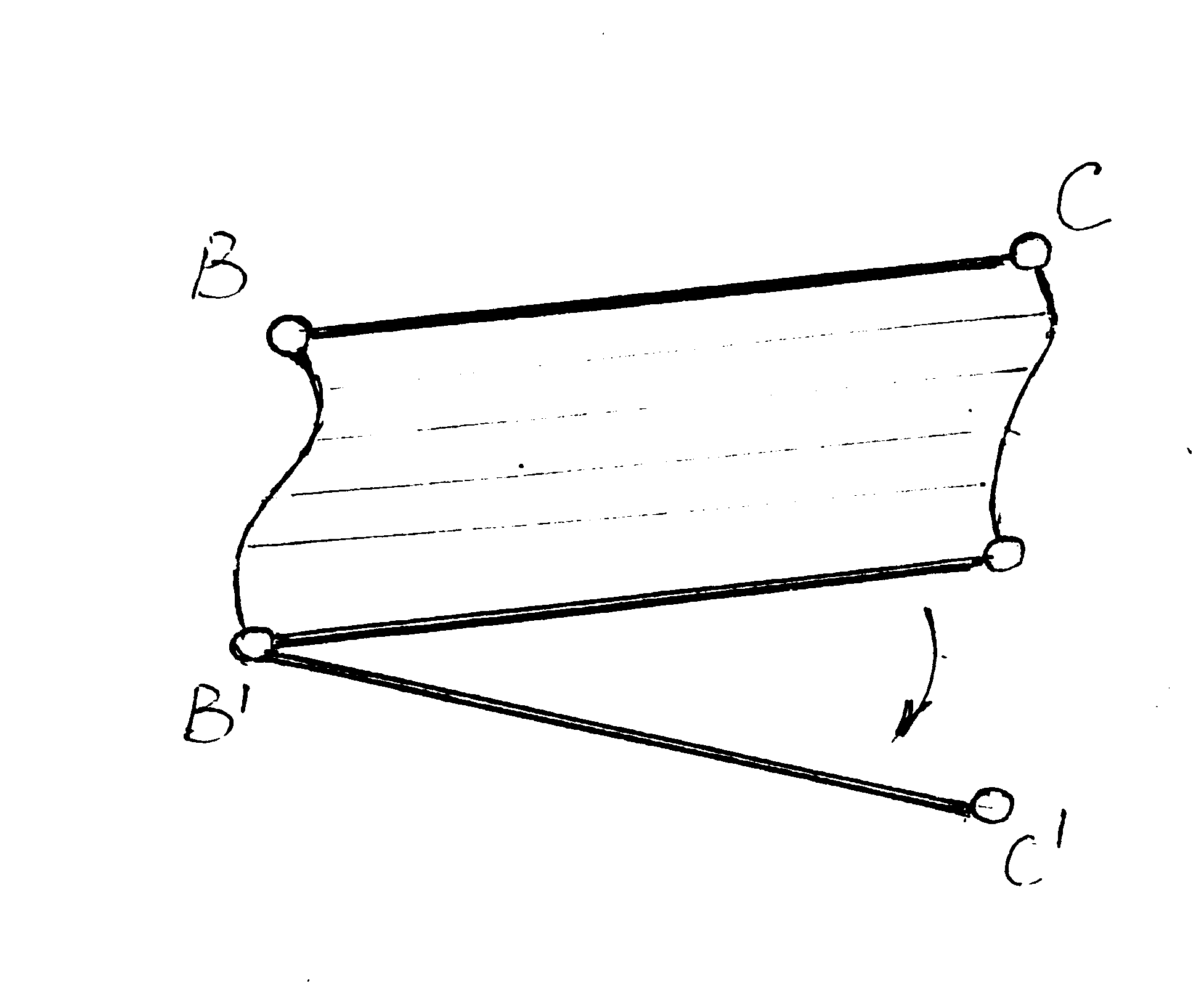
Точка В₃ – это точка кулисы 3 , которая в данном положении механизма проецируется в центр шарнира. Звенья 2 и 3 образуют поступательную пару ( V_B2 не равна V_B3 ). При написании векторных равенств для скоростей и ускорений точки В₃ раскладываем движение кулисы (второй способ разложения движения) на переносное вращательное движение вместе со звеном 2 и на относительное поступательное кулисы 3 по звену 2 . Относительная скорость V_B3B2 параллельна оси направляющих кулисы ( ВС). Равенство для определения скорости точки В₃ имеет вид

_ _ _

При этом угловая скорость звена 2 (т.к. переносное движение вращательное) не равна нулю, поэтому необходимо будет учитывать кориолисово ускорение.

Так как в рассматриваемом механизме звено 3 вращается вокруг точки С, то абсолютная скорость V_B3 ВС . Или, согласно 1-му способу разложения движения, можно записать

_ _ _

На плане скоростей (рис. 13б) из полюса откладываем произвольный отрезок pв_1,2 перпендикулярно АВ в направлении ₁. Тогда масштабный коэффициент скоростей _V = V_B1/ (pв₁). Через точку в_1,2 проводим прямую, параллельную ВС (согласно первому векторному равенству), а через полюс р (т.к. V_C = 0) – линию, перпендикулярную ВС (согласно второму равенству). Точка пересечения этих прямых и есть точка в₃ , а отрезок pв₃ изображает в выбранном масштабе скорость точки В₃ кулисы. Тогда V_B3 = (pb₃) _V.

Построение плана ускорений начинаем с изображения ускорения точки В_1,2 (центр шарнира). Так как ₁ = const , то

[м/с²].

На механизме это ускорение направлено по кривошипу АВ от В к А (рис.13, в). При этом

_а = [ ]

Для определения ускорения точки В₃ кулисы составляем два векторных равенства (как и для скорости):

_ _ _ _

_ _ _ _

Величина кориолисова ускорения определяется по формуле

а_B3B2 = 2 _пер V _{отн =} 2 ₂ V _{В3В2 ,}

где _{2 =} ₃ = _; V _В3В2 = ( в₂в₃ )·_{V .}

Следовательно, отрезок, изображающий это ускорение на плане ускорений, будет равен:

К_В3В2 = = ,

где  =

Направление кориолисова ускорения а^к_В3В2 находится путем поворота относительной скорости V_В3В2 на 90^о в направлении переносного вращения, т.е. в направлении вращения кулисы. Для определения направления вращения кулисы надо вектор относительной скорости V_B3C (или соответствующий ему отрезок cв₃ ) перенести с плана скоростей в точку В₃ кулисы и найти соответствующее этому направление вращения вокруг точки С (рис. 13, а).

На плане скоростей относительной скорости V_B3B2 соответствует отрезок ( в₂в₃ ) со стрелкой в сторону в₃ . Этот отрезок и надо поворачивать на 90^о в сторону ₃ , как показано на рис. 12, где полученное направление кориолисова ускорения а^к _B3B2 показано пунктиром.

Относительное ускорение а^r_B3B2 в поступательной паре известно по направлению: в данном случае а^r_B3B2  ВС.

Входящее во второе векторное равенство нормальное ускорение

аⁿ_B3C = (соответствующий вектор на плане ускорений n_{B3C =} [мм] ) направлено к центру вращения, т.е. от точки В к точке С , а а ^t_B3C  ВС.

Согласно векторным равенствам строим план ускорений (рис. 13, в). Через точку в_1,2 проводим прямую, параллельную найденному направлению а^к_В3В2, и на ней откладываем подсчитанный отрезок К_{В3В2 .} Через конец этого отрезка проводим прямую, параллельную ВС (направление а^r_B3B2 ). Затем из полюса плана ускорений ( т.к. а _С = 0 ) откладываем отрезок n_B3C (  ВС), а через его конец проводим прямую,  ВС (направление а^t _B3C). Точка пересечения этой прямой и прямой, проведенной  ВС через конец отрезка К_В3В2, и есть точка в₃ . Тогда а_B3 = (в₃) _а , а тангенциальное ускорение а^t _B3C = t_B3C _а._.

Для крайнего положения механизма планы скоростей и ускорений показаны на рис. 14.

Здесь V_B3 = 0. Следовательно, ₃ = 0, а поэтому а^к_B3B2 = 0 и аⁿ_B3C = 0.

Точки кулисы имеют только тангенциальные ускорения.