29.Бірінші ретті, біртекті, дербес туындылы сызықты диф-дық теңдеу. Жалпы шешім. Коши есебі.

-коэф, олар белгілі функциялар. -тәуелсіз айнымалылар.

Егер

симметриялық жүйенің жалпы интегралдар системасы болса, онда

үзіліссіз дифференциалданатын -функциясы (1)теңдеуінің жалпы шешімі болады.

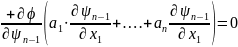
Олай болса теңдеуінің шешімі және бұл теңдеудің жалпы шешімі д.а.

Коши есебі (1) теңдеу үшін мынадай шарт беріледі.

(1)теңдеудің (3) шартты қанағаттандыратын шешімін табуды Коши есебі деп аталады.

- қандай да берілген алғашқы мән.

- берілген белгілі функция.

Геомертиялық тілде Коши есебі келесі шартты білдіреді.

(1)-теңдеудің шешімдері әртүрлі беттер құрайды. Олар интегралдық беттер деп атайды. Осы интегралдық беттердің ішінен беті арқылы өтетін интегралдық шешімді табуымыз керек.

9.Біртекті сызықты д.Т жүйесі. Шешімдерінің қасиеттері.

1° - біртекті жүйенің шешімі болса, оның кез-келген тұрақтыға көбейтіндісі де біртекті жүйенің шешімі болады.

2° егер біртекті жүйенің шешімдері болса, онда олардың қосындысы да айырмасы да біртекті жүйенің шешімдері болады.

Дәлелдеуі:

Осы 1°, 2° қасиеттен келесі салдар шығады.

Салдар 1: егер біртекті жүйенің шешімдері болса, онда олардың кез-келген сызықты өрнегі де біртекті жүйенің болады. Мұнда

Салдар 2: (1)

(1)жүйенің барлық шешімдерінің жиыны сызықты кеңістік құрайды және бұл сызықтық кеністіктің өлшемі -ге тең.

Біртекті жүйенің жалпы шешімі келесі түрде жазылады.

Мұнда -еркін тұрақтылар. Ал -біртекті жүйенің фундаментальді шешімдер системасы.

12.Туындысы бойынша шешілген бірінші ретті дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема. Мәндес интергралдық теңдеу

теңдеулер.

Коши есебі

F(x,y), (x,y)€П={(x,y): }

Aн. (x, )€ П нүктелері үшін қандай да бір ∃>0 тұрақтысы мына шарт орындалса келесі теңсіздік орындалса онда f(x,y) ф-сы П төртбұрышында Липшица шартын у аргументі б/ша қанағат-ды.Ескeрту: f(x,y) ф-сы ж/е бұл ф-ның П төртұрышында үзіліссіз болса f(x,y) ф-сы у бойынша Липшица шартынқанағат-ды.

ТҺ.(1) ші (2) Коши есебінің шешімінің бар болуы ж/е жалғыздығы туралы теорема. Егер (1)-ші теңдеуде f(x,y) ф-сы келесі шарттарды қанағат-са 1) f(x,y)ϵC(П) үзіліссіз П төртбұрышында болса, 2) f(x,y) ф-сы П төртұрышында у аргументі б/ша Липшица шартын қанағат-са,онда (1)-шi теңдеудің (2)-ші алғашқы шартты қанағ-н сегментінде анықталған 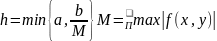жалғыз шешімі табылады.

Тһ дәлелдеуі. (1-ші пункт)(1),(2) Коши есебі келесі теңдеуге эквивалентті мәндес (3)-интегралдық теңдеу.Егер белгісіз ф-я интеграл таңбасының астында тұрса онда теңдеу мәндес интегралдық теңдеу деп аталады. (1),(2)~(3) (1) теңдеуді интегралдасақ: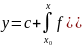 мәнін қойсақ (3) –теңдеу шығады. Керісінше (3) интегралдық теңдеуді дифф-сақ яғни х б/ша туындысын алсақ, онда (1) теңдеу шығады (2) шарттың орындалатыны көрініп тұр. Біз теореманы (3) интегралдық теңдеу үшін дәлелдейміз.

13.Туынды бойынша шешілген бірінші ретті Дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема. Функционалдық тізбектің құрылуы .

теңдеулер.

Коши есебі

F(x,y), (x,y)€П={(x,y): }

Aн. (x, )€ П нүктелері үшін қандай да бір ∃>0 тұрақтысы мына шарт орындалса келесі теңсіздік орындалса онда f(x,y) ф-сы П төртбұрышында Липшица шартын у аргументі б/ша қанағат-ды.Ескeрту: f(x,y) ф-сы ж/е бұл ф-ның П төртұрышында үзіліссіз болса f(x,y) ф-сы у бойынша Липшица шартынқанағат-ды.

ТҺ.(1) ші (2) Коши есебінің шешімінің бар болуы ж/е жалғыздығы туралы теорема. Егер (1)-ші теңдеуде f(x,y) ф-сы келесі шарттарды қанағат-са 1) f(x,y)ϵC(П) үзіліссіз П төртбұрышында болса, 2) f(x,y) ф-сы П төртұрышында у аргументі б/ша Липшица шартын қанағат-са,онда (1)-шi теңдеудің (2)-ші алғашқы шартты қанағ-н сегментінде анықталған жалғыз шешімі табылады.

Тһ дәлелдеуі. Келесі функциялар тізбегін анықтаймыз.

Біз функциялар тізбегің құрдық. Бұл – функционалдық тізбек. Бұл функцияның тізбегі аралығында анықталған, себебі

Бізде интегралдың жоғары шегі айнымалы болғандықтан функционалдық тізбектің мүшелері үзіліссіз функциялар болады.