
- •3.Айнымалылары ажыратылатын теңдеулер
- •5. Біртекті дифференциалдық теңдеулерге келтірілетін теңдеулер.
- •6.Бірінші ретті сызықты дифференциалдық теңдеулер
- •8. Бернулли теңдеуі
- •9. Толық дифференциалды теңдеулер
- •18. Лагранж теңдеуі
- •19. Клеро теңдеуі
- •25.Жоғарғы ретті, біртекті сызықты диф.Теңдеу. Вронскиан және оның қасиеттері.
- •27. Коэф-рі тұрақты, сызықты біртекті диф-дық теңдеу. Эйлер әдісі сипаттауыш теңдеу.
- •28. Коэф-рі тұрақты, сызықты біртекті диф-дық теңдеу. Жай түбірлер.
- •30.Бірінші ретті квази сызықты дербес туындылы диф-дық теңдеу. Коши есебі.
- •29.Бірінші ретті, біртекті, дербес туындылы сызықты диф-дық теңдеу. Жалпы шешім. Коши есебі.
- •9.Біртекті сызықты д.Т жүйесі. Шешімдерінің қасиеттері.
- •12.Туындысы бойынша шешілген бірінші ретті дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема. Мәндес интергралдық теңдеу
- •13.Туынды бойынша шешілген бірінші ретті Дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема. Функционалдық тізбектің құрылуы .
- •14. Туынды бойынша шешілген бірінші ретті Дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема.Функционалдық тізбектің жинақтылығы.
- •15. Туынды бойынша шешілген бірінші ретті Дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема.Шешімнің табылуы.
- •16. Туынды бойынша шешілген бірінші ретті Дт үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема.Шешімнің жалғыздығы.
3.Айнымалылары ажыратылатын теңдеулер
Айнымалылары ажыратылатын теңдеулердің жалпы түрі былай жазылады:
 (1)
(1)
(1)теңдеу– дифференциалдық түрде жазылған айнымалылары ажыратылатын теңдеу. Мұнда x пен y бірдей дәрежеде еніп тұр.

 (2)
(2)
Бұл келтіру айнымалыларды ажырату тәсілі деп аталады. Жалпы, айнымалыларды ажырату деп dx-тың алдында тек х-қа тәуелді, ал dy-тың алдында тек у-ке тәуелді функциялардың тұруын қамтамасыз етуді айтады.
 (3)
(3)
(3) берілген теңдеудің жалпы интегралы.
Ескерту: Біз дифф−қ теңдеудің шешімін интеграл алуға келтірсек, оны квадратурада шешуге келтірдік дейміз.
5. Біртекті дифференциалдық теңдеулерге келтірілетін теңдеулер.
1)
Бұл
теңдеуде
 ,
,
 ,
,
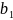 ,
,
 ,
,
 ,
,
 -
берілген нақты сандар.
-
берілген нақты сандар.

бұл теңдеуді шешу үшін келесі жүйені қарастырамыз

 шешімі
осы жүйенің 2 теңдеуден тұрады. Осы
теңдеудің шешімін табамыз. Содан соң
шешімі
осы жүйенің 2 теңдеуден тұрады. Осы
теңдеудің шешімін табамыз. Содан соң
 ауыстыруын жасаймыз. Мұнда
ауыстыруын жасаймыз. Мұнда
 -
-
 -тың
орнына келген жаңа айнымалы, ал
-тың
орнына келген жаңа айнымалы, ал
 -
-
 -тың
орнына. Бұл кезде берілген теңдеу
және
айнымалылары бойынша біртекті теңдеуге
келеді.
-тың
орнына. Бұл кезде берілген теңдеу
және
айнымалылары бойынша біртекті теңдеуге
келеді.
 Бұл біртекті теңдеудің шешімін тауып,
мен
-ның
орнына қолданылған ауыстырымды
пайдаланып,
пен
айнымалысына көшеміз. Сонда берілген
теңдеудің шешімі шығады.
Бұл біртекті теңдеудің шешімін тауып,
мен
-ның
орнына қолданылған ауыстырымды
пайдаланып,
пен
айнымалысына көшеміз. Сонда берілген
теңдеудің шешімі шығады.
2)
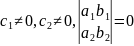
Бұл
кезде
 немесе
немесе
 ауыстырылуын пайдаланамыз. Сонда теңдеу
айнымалылары ажыратылатын теңдеуге
келеді.
ауыстырылуын пайдаланамыз. Сонда теңдеу
айнымалылары ажыратылатын теңдеуге
келеді.
6.Бірінші ретті сызықты дифференциалдық теңдеулер
Белгісіз функция мен оның туындысы сызықты түрде, яғни бірінші дәрежеде байланысқан теңдеуді сызықты дифференциалдық теңдеу деп атайды.
 (1)
(1)
 берілген
белгілі функциялар.
берілген
белгілі функциялар.
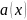 ,
,
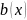 -
теңдеудің коэф.
-
теңдеудің коэф.
 -
теңдеудің бос мүшесі немесе оң жағы деп
аталады.
-
теңдеудің бос мүшесі немесе оң жағы деп
аталады.
Егер
 болса, онда теңдеу біртекті сызықты
теңдеу д.а.
болса, онда теңдеу біртекті сызықты
теңдеу д.а.
Егер
 болса, онда теңдеу әртектісызықты теңдеу
д.а.
болса, онда теңдеу әртектісызықты теңдеу
д.а.
Біртекті
теңдеу.
 (2)
(2)
(1)- ші теңдеуге сәйкес біртекті теңдеу д.а. Бұл айнымалылары ажыратылатын теңдеу.
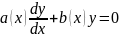


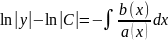


(3) теңдеу (1) теңдеудің жалпы теңдеуі.
8. Бернулли теңдеуі
Мына түрдегі теңдеуді
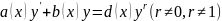
Бернулли
теңдеуі деп атайды.
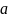 ,b,
,b, - берілген
белгілі функциялар, олар Бернулли
теңдеуінің коэф-і.
- берілген
белгілі функциялар, олар Бернулли
теңдеуінің коэф-і.
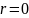 ;
;
 сызықты теңдеу шығады.
сызықты теңдеу шығады.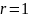 ;
біртекті сызықты теңдеу шығады.
;
біртекті сызықты теңдеу шығады.
Бұл
теңдеуді шығару үшін теңдеуді
 -осыған
бөлеміз.
-осыған
бөлеміз.
 -
нақты сан.
-
нақты сан.



 –сызықты
теңдеу.
–сызықты
теңдеу.
Сызықты
теңдеуді шешіп
 -ті
табамыз. Қорыта айтқанда Бернулли
теңдеуі сызықтық теңдеуге келтіріледі.
-ті
табамыз. Қорыта айтқанда Бернулли
теңдеуі сызықтық теңдеуге келтіріледі.
9. Толық дифференциалды теңдеулер
 (1)
(1)
Дифференциалдар
арқылы жазылған теңдеуді қарастырайық.
Бұл теңдеуге
пен
бірдей дәрежеде еніп тұр.
 ,
,
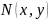 ,берілген
және
айнымалыларынан тәуелді функциялар,
яғни көп айнымалы функциялар.
,берілген
және
айнымалыларынан тәуелді функциялар,
яғни көп айнымалы функциялар.
Анықтама:
Егер (1)- теңдеудің сол жағы қандай да
бір
 функциясының толық дифф-лы болса, яғни
функциясының толық дифф-лы болса, яғни
 теңдік орындалса, онда (1)-ші теңдеу-
толық дифф-дық теңдеу деп аталады. Бұл
кезде
теңдік орындалса, онда (1)-ші теңдеу-
толық дифф-дық теңдеу деп аталады. Бұл
кезде
 (1)-ші теңдеудің жалпы интегралы болып
табылады.
(1)-ші теңдеудің жалпы интегралы болып
табылады.
18. Лагранж теңдеуі
 (1)
(1)
түріндегі теңдеуді Лагранж теңдеуі деп атаймыз.

Бұл теңдеуді параметр енгізу арқылы шығарамыз.




бойынша
сызықты теңдеу шықты. Бұдан
 -
функциясын
табамыз.
-
функциясын
табамыз.
 параметр
бойынша жазылған Лагранж теңдеуінің
шешімі.
параметр
бойынша жазылған Лагранж теңдеуінің
шешімі.
Ескерту: Лагранж теңдеудің ерекше шешімдері болуы да болмауы да мүмкін.
Ерекше шешім дегеніміз – жалғыздық шарты бұзылған шешімді айтамыз.
