15) Туынды бойынша шешілген 1 ретті д.Т.Үшін Коши есебінің шешімі бар болуы ж/не жалғыздығы туралы теорема. Шешімнің табылуы.
1.Негізгі ұғымдар. Дифференциалдық теңдеу деп әдетте тәуелсіз айнымалыны, ізделінетін функцияны және оның әр түрлі реттегі туындыларын (дифференциалдарын) байланыстыратын теңдеуді айтады.Теңдеуге кіретін туындының (дифференциалдың) ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.Егер ізделінетін функция тек бір аргументтен тәуелді болса, онда дифференциалдық теңдеу жай деп, ал бірнеше аргументтен тәуелді болса дербес туындылы дифференциалдық теңдеу деп аталынады. Айтылғанға сай n-ші ретті жай дифференциалдық теңдеу жалпы түрде былай жазылады:
. ( 1)
Мұндағы х-тәуелсіз айнымалы, у-ізделінетін функция, ал туындылар. Егер (1) теңдеуде екі тәуелсіз айнымалы х1 , х2 , бір ғана ізделінетін функция болса , онда ол n-ші ретті дербес туындылы дифференциалдық теңдеу болар еді де, былай жазылар еді: .
Егер (1) теңдеуде n=1болса, онда алынған теңдеу
бірінші ретті дифференциалдық теңдеу деп, ал қалған болған жағдайларда жоғары ретті дифференциалдық теңдеу деп аталады. Егер (2) теңдеу бойынша шешілетін болса, онда алынған теңдеу. (3) туындысы бойынша (туынды қатысты) шешілген бірінші ретті дифференциалдық теңдеу деп аталады. (3) теңдеудегі фуекциясын кейінде берілген Д обылсында бір мәнді, қос аргумент бойынша үздіксіз деп есептейміз. Д - облысы (3) теңдеудің анықталу облысы деп аталады. Егер функциясы қандайда болмасын бір нүктесінің аймағында ақырсыздыққа (шексіздікке) айналса, онда теңдеуі (3) қарағанда төңкерілген деп аталады. функциясының осындай нүктелері мен оның анықталмаған, бірақ үздіксіздік қасиеті бойынша анықталуға келетін нүктелерінің жиынын да (3) теңдеудің анықталу обылысына жатқызамыз.
16) Туынды бойынша шешілген 1 ретті д.Т.Үшін Коши есебінің шешімі бар болуы ж/не жалғыздығы туралы теорема. Шешімнің жалғыздығы.
1.Негізгі ұғымдар. Дифференциалдық теңдеу деп әдетте тәуелсіз айнымалыны, ізделінетін функцияны және оның әр түрлі реттегі туындыларын (дифференциалдарын) байланыстыратын теңдеуді айтады.Теңдеуге кіретін туындының (дифференциалдың) ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.Егер ізделінетін функция тек бір аргументтен тәуелді болса, онда дифференциалдық теңдеу жай деп, ал бірнеше аргументтен тәуелді болса дербес туындылы дифференциалдық теңдеу деп аталынады. Айтылғанға сай n-ші ретті жай дифференциалдық теңдеу жалпы түрде былай жазылады:
. ( 1)
Мұндағы х-тәуелсіз айнымалы, у-ізделінетін функция, ал туындылар. Егер (1) теңдеуде екі тәуелсіз айнымалы х1 , х2 , бір ғана ізделінетін функция болса , онда ол n-ші ретті дербес туындылы дифференциалдық теңдеу болар еді де, былай жазылар еді: .
Егер (1) теңдеуде n=1болса, онда алынған теңдеу
бірінші ретті дифференциалдық
теңдеу деп, ал қалған
болған жағдайларда жоғары
ретті дифференциалдық
теңдеу деп аталады. Егер (2) теңдеу
бойынша шешілетін болса, онда алынған
теңдеу.
(3) туындысы бойынша (туынды қатысты)
шешілген бірінші ретті дифференциалдық
теңдеу деп аталады. (3) теңдеудегі
фуекциясын кейінде берілген Д обылсында
бір мәнді, қос аргумент бойынша үздіксіз
деп есептейміз. Д - облысы (3) теңдеудің
анықталу облысы деп
аталады. Егер
функциясы қандайда болмасын бір
нүктесінің аймағында ақырсыздыққа
(шексіздікке) айналса, онда
теңдеуі (3) қарағанда
төңкерілген деп аталады.
функциясының осындай нүктелері мен
оның анықталмаған, бірақ үздіксіздік
қасиеті бойынша анықталуға келетін
нүктелерінің жиынын да (3) теңдеудің
анықталу обылысына жатқызамыз.
17) Туынды бойынша шешілмеген теңдеу.Параметр енгізу әдісі.
18) Лагранж теңдеуі.
19)Клеро теңдеуі.
20) Реті төменд. жоғарғы ретті
д.т.тәуелсіз айнымалылары жоқ теңдеу.
21) Реті төменд. жоғарғы ретті д.т белгісіз фукция жоқ теідеу
22) Жоғары ретті біртекті сыз.д.т.сыз тәу.ж/не сыз. тәуелсіз функ-лар системасы.
23) Жоғарғы ретті біртекті
сыз.д.т.фунд шеш жүйесі,сыз д.т.опретаордың
қасиеті.
24) Жоғарғы ретті біртекті сыз.д.т.шешімдердің қасиеттері,жалпы шешімнің құрылуы.
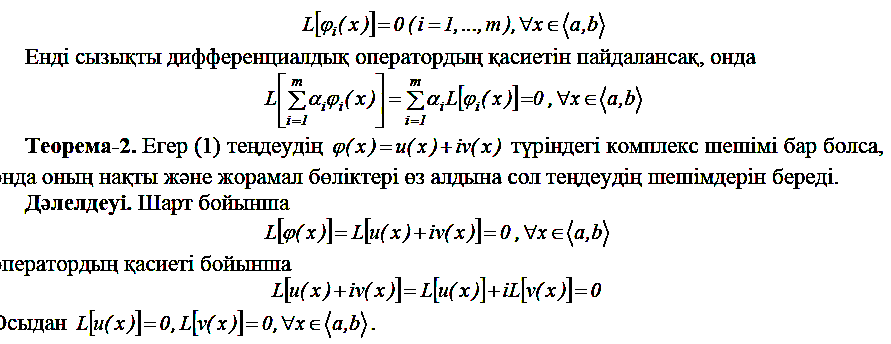
n-ші ретті біртекті сыз дифф
т-дің жалпы шешімі келесі түрде жазлады
25) Жоғарғы ретті біртекті
сыз.д.т Вронскиан ж/не оның қасиеттері.
26) Жоғарғы ретті біртекті
сыз.д.т остр-лиувилль.
немесе
27) Коэф тұрақты сыз бірт
д.т.Эйлер әдісі Сипаттауыш теңдеу
28) Коэф тұрақты.сыз бірт...жай түбірлер
29) Коэф тұрақты.комлекс түбірлер,Эйлер форм-сы нақты шешулерді бөліп шығару.
30)коэф тұрақты бірт сыз д.т. еселі түбірлер
