
- •6 Второе начало и необратимость процессов
- •6.4 Эксергия и анергия
- •6.9 Влияние окружающей среды на преобразование энергии
- •6.10 Баланс энтропии для стационарного поточного процесса
- •7 Термодинамические свойства чистых
- •7.1 Термическое уравнение состояния. Р, , t – поверхность
- •7.6 Внутренняя энергия Ван-дер-Ваальсовского газа
- •7.8 Экспериментальные изотермы
- •7.9 Фазовые превращения
- •8 Влажный пар
- •8.3 Изохорный процесс изменения состояния пара
- •9.4 Изобарный процесс изменения состояния водяного пара
- •8.5. Изотермический процесс изменения состояния водяного пара
- •9 Влажный газ
- •9.2 Экстенсивные свойства влажного воздуха
- •9.5 Основные процессы влажного воздуха
- •10. Третье начало термодинамики и элементы статистической термодинамики
- •11 Флуктуации
10. Третье начало термодинамики и элементы статистической термодинамики
10.1 Третье начало термодинамики
При
приближении к абсолютному нулю
 в поведении различных реальных веществ
проявляется закономерность, играющая
важную роль в термодинамике и состоящая
в том, что при этом энтропия тела в любом
равновесном состоянии не зависит от
температуры, объема и других параметров
состояния термодинамической системы
в поведении различных реальных веществ
проявляется закономерность, играющая
важную роль в термодинамике и состоящая
в том, что при этом энтропия тела в любом
равновесном состоянии не зависит от
температуры, объема и других параметров
состояния термодинамической системы
,
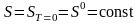 .
.
Последний
факт непосредственно не связан с первым
и вторым началами термодинамики и носит
название тепловой теоремы Нернста.
Из тепловой теоремы Нернста следует,
что вблизи абсолютного нуля температуры
теплоемкости Ср
и
 ,
определяемые из соотношений
,
определяемые из соотношений
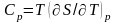 и
и
 ,
равны нулю, так как вторые сомножители
в приведенных зависимостях
,
равны нулю, так как вторые сомножители
в приведенных зависимостях
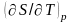 и
и
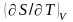 вблизи абсолютного нуля температуры
равны нулю.
вблизи абсолютного нуля температуры
равны нулю.
Вообще,
при
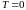 теплоемкость любого процесса равна
нулю
теплоемкость любого процесса равна
нулю
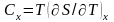 =0.
=0.
При энтропия любого вещества в жидком и твердом состояниях будут равны, а энтропия смеси из 1 моля вещества А и 1 моля вещества В будет равна энтропии 1 моля их химического соединения АВ.
Постоянство
энтропии при
 означает, что в области абсолютного
нуля температуры всегда
.
Следовательно, любая из изотерм совпадает
с адиабатой
означает, что в области абсолютного
нуля температуры всегда
.
Следовательно, любая из изотерм совпадает
с адиабатой
 .
Таким образом, всякая изотермическая
система ведет себя как адиабатная, а
значит, она может совершать работу лишь
за счет своих внутренних ресурсов при
изменении ее внутренней энергии. То
есть любая адиабатная система одновременно
и изотермична. Следовательно, за счет
адиабатного расширения термодинамической
системы достигнуть абсолютного нуля
температуры невозможно. Так же нельзя
достигнуть абсолютного нуля температуры
путем отвода тепла, так как каждое из
тел, участвующих в теплообмене, не
изменяет свою энтропию, то есть перестает
отдавать тепло окружающей среде.
.
Таким образом, всякая изотермическая
система ведет себя как адиабатная, а
значит, она может совершать работу лишь
за счет своих внутренних ресурсов при
изменении ее внутренней энергии. То
есть любая адиабатная система одновременно
и изотермична. Следовательно, за счет
адиабатного расширения термодинамической
системы достигнуть абсолютного нуля
температуры невозможно. Так же нельзя
достигнуть абсолютного нуля температуры
путем отвода тепла, так как каждое из
тел, участвующих в теплообмене, не
изменяет свою энтропию, то есть перестает
отдавать тепло окружающей среде.
На основании этого Планк пришел к выводу:
При температуре абсолютного нуля энтропия всех веществ в состоянии равновесия независимо от давления, плотности и фазы обращается в нуль.
 .
(10.1)
.
(10.1)
Это и есть основное содержание третьего начала термодинамики.
Газы при малых, но ощутимых давлениях, конденсируются при температурах значительно превышающих температуру . Поэтому третье начало термодинамики в основном относится к конденсированным состояниям (то есть к твердым и жидким телам). Из всех веществ только гелий II остается жидкостью при и давлениях порядка 105 Па. Все другие вещества при этом находятся в твердом состоянии.
Из третьего начала термодинамики следует важное следствие.
Вблизи абсолютного нуля все термодинамические свойства, характеризующие равновесное состояние термодинамической системы, перестают зависеть от температуры.
Это означает, что частные производные термодинамических параметров (внутренней энергии, энтальпии, давления, удельного объема и др.) по температуре при обращаются в нуль.
Третье начало термодинамики представляет собой макроскопическое проявление квантовых свойств материи. Поэтому в этом смысле его можно считать законом достаточно точным.
На основании третьего начала термодинамики по известной величине теплоемкости можно вычислить абсолютное значение термодинамических функций.
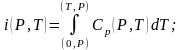 (10.2)
(10.2)
 (10.3)
(10.3)
При
низких температурах (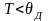 )
изохорная мольная теплоемкость твердых
кристаллических тел равна
)
изохорная мольная теплоемкость твердых
кристаллических тел равна
 ,
,
где
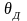 – температура Дебая,
– температура Дебая,
 – универсальная газовая постоянная
– универсальная газовая постоянная
Найденная по этой зависимости величина представляет собой решеточную теплоемкость, обусловленную движением атомов (ионов), находящихся в узлах кристаллической решетки.
Температура Дебая определяется из условия
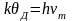 ,
,
где
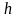 – постоянная Планка,
= 6,625510-27 эрг. с;
– постоянная Планка,
= 6,625510-27 эрг. с;
 – наибольшая частота упругих волн,
распространяющихся в твердом теле
(звуковых волн);
–
постоянная Больцмана.
– наибольшая частота упругих волн,
распространяющихся в твердом теле
(звуковых волн);
–
постоянная Больцмана.
При температурах близких к абсолютному нулю нужно учитывать, кроме того, электронные степени свободы, то есть электронную составляющую теплоемкости.
При
высоких температурах ( )
теплоемкость твердых тел постоянна и
практически определяется законом
Дюлонга и Пти
)
теплоемкость твердых тел постоянна и
практически определяется законом
Дюлонга и Пти
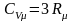 .
.
10.2 Недостижимость абсолютного нуля
Ранее было показано, что адиабатное расширение является наиболее эффективным способом получения «холода», сопровождающееся наибольшим понижением температуры расширяющегося рабочего тела.
Допустим, что начальное состояние термодинамической системы (рабочего тела) определяется параметрами (Р1, Т1). Ее энтропия в этом состоянии
 .
.
При обратимом адиабатном (изоэнтропном) процессе энтропия рабочего тела остается без изменения. Поэтому для любого состояния Т Т1 изоэнтропного процесса справедливо равенство
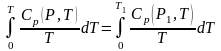 .
.
При Т = 0 интеграл в левой части обращается в нуль.
Таким образом, если абсолютный нуль в процессе изоэнтропного расширения достижим, то и интеграл, стоящий в правой части, должен автоматически быть равен нулю. Однако это невозможно, ибо теплоемкость тела при любой конечной температуре положительна и конечна.
Следовательно, абсолютный нуль недостижим. Тогда третье начало термодинамики может быть сформулировано так:
Не существует обратного термодинамического процесса, по которому можно было бы охладить термодинамическую систему до абсолютного нуля температуры. Однако приблизиться к нему сколь угодно близко возможно.
Это
утверждение не имеет внутренней
логической связи со вторым началом
термодинамики. Однако оно приводит нас
к в выводу о том, что
невозможно осуществить тепловую машину
Карно с температурой источника тепла,
воспринимающего компенсацию второго
рода при температуре
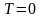 .
.
Идеальные
газы не удовлетворяют теореме Нернста.
По определению газовая постоянная
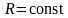 ,
а по процессу мы выбрали
.
Правая часть уравнения является
постоянной величиной
,
а по процессу мы выбрали
.
Правая часть уравнения является
постоянной величиной
 .
.
Следовательно,
теплоемкость идеального газа при
не обращается в ноль, а разность
 как этого требует теорема Нернста.
как этого требует теорема Нернста.
10.3 Статистическая природа второго начала термодинамики
При реализации системой необратимых термодинамических процессов ее конечное состояние отличается от начального заметно большей величиной энтропии. Причем эта разность тем больше, чем выше степень необратимости присутствующих при реализации процесса диссипативных моментов. Это означает, что каждое последующее состояние системы более вероятно предшествующему.
Пусть
система состоит из N
одинаковых молекул, где их число
достаточно велико. В этом случае одно
и тоже макроскопическое состояние
термодинамической системы (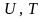 )
может обеспечиваться различным
распределением энергии между отдельно
взятыми частицами – молекулами, то
есть через различные ее микросостояния.
)
может обеспечиваться различным
распределением энергии между отдельно
взятыми частицами – молекулами, то
есть через различные ее микросостояния.
Каждое
конкретно взятое микросостояние
отличается от других значениями
координат
 и импульсов
и импульсов
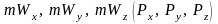 всех
всех
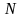 молекул, из которых состоит система.
Рассмотрим некоторое «замороженное»
микросостояние системы. Тогда из всех
молекул их
молекул, из которых состоит система.
Рассмотрим некоторое «замороженное»
микросостояние системы. Тогда из всех
молекул их
 число будет иметь энергию
число будет иметь энергию
 ,
,
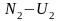 и так далее, где
и так далее, где
 – энергетические уровни конкретных
молекул – частиц молекулярной системы.
В соответствии тем, что мы рассматривали
микросостояния, обеспечивающие
конкретное макросостояние, должно
выполняться очевидное равенство
– энергетические уровни конкретных
молекул – частиц молекулярной системы.
В соответствии тем, что мы рассматривали
микросостояния, обеспечивающие
конкретное макросостояние, должно
выполняться очевидное равенство
 .
.
Общее число микросостояний, обеспечивающих данное макросостояние будет равно общему числу перестановок N ! поделенному на число перестановок молекул внутри каждой из характерных по энергиям групп
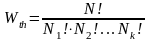 .
(10.4)
.
(10.4)
Величину
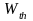 по предложению Планка называют
термодинамической вероятностью.
Численное значение
больше единицы во много раз. Она
характеризует возможность реализации
определенного распределения молекул
по энергиям или вероятность данного
молекулярного состояния.
по предложению Планка называют
термодинамической вероятностью.
Численное значение
больше единицы во много раз. Она
характеризует возможность реализации
определенного распределения молекул
по энергиям или вероятность данного
молекулярного состояния.
Хаотичность
теплового движения молекул обуславливает
равновероятность каждого из микросостояний,
отвечающему условию
 .
Это означает, что частота появления
микросостояний с одинаковым распределением
молекул по энергиям будет тем большей,
чем больше число способов, обеспечивающих
данное распределение, следовательно,
тем больше термодинамическая вероятность
данного микросостояния. Таким образом,
состояние
системы с максимальным значением
термодинамической вероятности
представляют собой равновесные состояния
системы. Все другие состояния системы,
вероятность которых меньше максимальной
будут неравновесными.
.
Это означает, что частота появления
микросостояний с одинаковым распределением
молекул по энергиям будет тем большей,
чем больше число способов, обеспечивающих
данное распределение, следовательно,
тем больше термодинамическая вероятность
данного микросостояния. Таким образом,
состояние
системы с максимальным значением
термодинамической вероятности
представляют собой равновесные состояния
системы. Все другие состояния системы,
вероятность которых меньше максимальной
будут неравновесными.
Отношение термодинамической вероятности данного молекулярного состояния к общему числу возможных микросостояний системы представляет собой вероятность W данного молекулярного состояния системы. В этом случае, очевидно, что W<1.
 . (10.5)
. (10.5)
Зная
вероятность
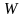 или термодинамическую вероятность
каждого из молекулярных состояний
системы, легко вычислить среднее
значение любой величины В,
зависящей от состояния системы
или термодинамическую вероятность
каждого из молекулярных состояний
системы, легко вычислить среднее
значение любой величины В,
зависящей от состояния системы
 , (10.6)
, (10.6)
где В – некоторая физическая величина, зависящая от координат и импульсов молекул данной системы. Суммирование в (11.6) производится по всем молекулярным состояниям.
10.4 Формула Больцмана
Рассмотрим
равновесный изотермический процесс
изменения состояния системы, в результате
которого объем системы
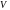 получает приращение
получает приращение
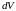 и становится равным
и становится равным
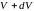 ,
а внутренняя энергия системы изменится
на величину произведенной работы
,
а внутренняя энергия системы изменится
на величину произведенной работы
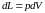 .
При этом произойдет дополнительное
изменение внутренней энергии системы,
связанное с изменением распределения
молекул по энергиям. Энергия каждого
микросостояния равна внутренней энергии
.
При этом произойдет дополнительное
изменение внутренней энергии системы,
связанное с изменением распределения
молекул по энергиям. Энергия каждого
микросостояния равна внутренней энергии
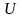 системы. Тогда изменение внутренней
энергии
системы. Тогда изменение внутренней
энергии
 при изменении числа микросостояний на
при изменении числа микросостояний на
 будет пропорционально относительному
изменению числа микросостояний
будет пропорционально относительному
изменению числа микросостояний
 .
Множитель f
введен из соображений размерности
.
Множитель f
введен из соображений размерности
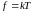 .
Индекс «*» означает, что рассуждение
относится к равновесным состояниям.
Тогда полное изменение внутренней
энергии молекулярной системы при
изотермическом процессе
.
Индекс «*» означает, что рассуждение
относится к равновесным состояниям.
Тогда полное изменение внутренней
энергии молекулярной системы при
изотермическом процессе
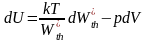 .
.
В соответствии с первым началом термодинамики
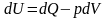 .
.
Приравнивая правые части, получим
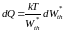 . (10.7)
. (10.7)
Из последнего
выражения (10.7) следует вывод, что
подведенная
к системе из вне энергия затрачивается
на изменение распределения молекул по
энергии.
Таким образом, подведенная энергия
связана с перераспределением вероятностей
микросостояний. Если процесс равновесный,
то
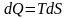 ,
а значит
,
а значит
 или
или
 .
.
Или после интегрирования
 .
(10.8)
.
(10.8)
В изолированной системе любое из состояний соответствует одному и тому же значению внутренней энергии, поэтому полученная зависимость может быть распределена и на неравновесные состояния
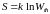 .
.
Из последнего
выражения следует, что энтропия всегда
положительна (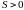 ),
так как
),
так как
 .
Значения
термодинамической вероятности и
вероятности состояния отличаются на
величину постоянного множителя, тогда
.
Значения
термодинамической вероятности и
вероятности состояния отличаются на
величину постоянного множителя, тогда
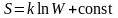 .
.
Энтропия изолированной системы пропорциональна натуральному логарифму вероятности состояния.
Последнее выражение принято называть формулой Больцмана. Из формулы Больцмана не следует, что энтропия – величина аддитивная.
Рассмотрим
составную систему, для которой
вероятность W
данного состояния равна произведению
вероятностей состояний
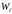 ,
составных частей
,
составных частей
 .
После логарифмирования получим
.
После логарифмирования получим
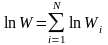
или 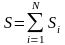 .
(10.9)
.
(10.9)
Зависимость (10.9) отражает аддитивность энторопии.
10.5 Статистическая формулировка второго начала термодинамики
В соответствии с формулой Больцмана при переходе системы из менее вероятного неравновесного состояния в более вероятное равновесное состояние ее энтропия возрастает
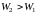 ,
,

или
 .
Или энтропия
системы в состояние равновесия
максимальна.
.
Или энтропия
системы в состояние равновесия
максимальна.
Рис.
10.1 Изменение энтропии
изолированной
системы во времени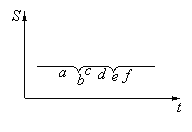
 .
Если система находится
в состоянии равновесия, то наиболее
вероятны процессы, при которых энтропия
системы не изменяется.
Следует понимать, что речь идет о
самопроизвольных процессах.
.
Если система находится
в состоянии равновесия, то наиболее
вероятны процессы, при которых энтропия
системы не изменяется.
Следует понимать, что речь идет о
самопроизвольных процессах.
Статистическая формулировка второго начала термодинамики, таким образом, утверждает, что в замкнутой системе процессы сопровождающиеся возрастанием энтропии являются наиболее вероятными.
Феноменологическая термодинамика утверждает, что такие процессы единственно возможны.
Различие в формулировках носит принципиальный характер. Статистическая формулировка второго начала предполагает возможность процессов, в результате которых система переходит из более вероятных в менее вероятные состояния, сопровождающиеся уменьшением энтропии. Несмотря на малую вероятность таких процессов при достаточно большом промежутке времени такое событие произойдет.
Каждое из состояний повторяется с частотой тем большей, чем больше ее вероятность, а ее энтропия во времени изменяется так, как показано на рисунке.
10.6 Статистическая формулировка второго и третьего
начала
Сказанное выше позволяет сформулировать толкования второго и третьего начала термодинамики
Запишем формулу Больцмана
; .
При стремление
молекулярная система переходит в свое
наилучшее энергетическое состояние,
в котором ее вероятность состояния
становится равной 1 единице, а энтропия
обращается в нуль.
Иными словами, при
 молекулярная система переходит от
хаоса к полному порядку.
В то же время, рассматривая энтропию
как меру беспорядка (хаоса) мы неизбежно
приходим к выводу, что в этом случае
молекулярная система переходит от
хаоса к полному порядку.
В то же время, рассматривая энтропию
как меру беспорядка (хаоса) мы неизбежно
приходим к выводу, что в этом случае
 .
.
10.7 Состояния с отрицательной температурой
Состояния с
отрицательной абсолютной температурой
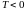 впервые были обнаружены в опытах с
фтористым литием. При наложении
электрического поля большинство ядерных
спинов ориентируются по полю и лишь
незначительная их часть из-за
взаимодействия друг с другом – против
поля. При быстром изменении направления
магнитного поля не все спины успевают
переориентироваться и поэтому в течение
некоторого очень малого времени
большинство спинов будет ориентировано
против магнитного поля. Это означает,
они будут распределены по энергетическим
уровням таким образом, при котором на
уровне с большей энергией число спинов
больше, чем на более низком энергетическом
уровне. Предположим, что энергия ядерного
спина в магнитном поле равна
впервые были обнаружены в опытах с
фтористым литием. При наложении
электрического поля большинство ядерных
спинов ориентируются по полю и лишь
незначительная их часть из-за
взаимодействия друг с другом – против
поля. При быстром изменении направления
магнитного поля не все спины успевают
переориентироваться и поэтому в течение
некоторого очень малого времени
большинство спинов будет ориентировано
против магнитного поля. Это означает,
они будут распределены по энергетическим
уровням таким образом, при котором на
уровне с большей энергией число спинов
больше, чем на более низком энергетическом
уровне. Предположим, что энергия ядерного
спина в магнитном поле равна
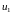 при ориентации по направлению магнитного
поля, и
при ориентации по направлению магнитного
поля, и
 при ориентации против поля.
при ориентации против поля.
Очевидно, что
будет выполняться неравенство
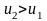 .
.
Допустим, что
число ядерных спинов – N.
Причем
из них ориентированы по полю, а
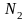 – против. Тогда общая энергия ядерных
спинов (пренебрегая энергией их
взаимодействия) будет равна
– против. Тогда общая энергия ядерных
спинов (пренебрегая энергией их
взаимодействия) будет равна
 .
.
Энергия взаимодействия
ядерных спинов не вносит заметного
вклада в энергетический баланс, но оно
имеет существенное значение, ибо может
привести и удержать на некоторое время
термодинамическую молекулярную систему
в состоянии с вышеотмеченным распределением
спинов. Благодаря ему, рассматриваемое
состояние может считаться статистически
равновесным, а значит подчиняющимся
закономерностям статистической
термодинамики. Такой вывод вытекает
из соотношения времен спин-спиновой и
спин-решетчатой релаксации. Спин-спиновая
релаксация имеет порядок времени
10-5 с,
спин-решетчатая релаксация –
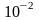 с.
с.
В этом случае
система спинов в промежутке времени
от
 с
до
с
после смены направления магнитного
поля может рассматриваться как
находящаяся в состоянии статистического
равновесия. Строго говоря, состояние
спиновой системы с ориентацией против
магнитного поля неравновесно и через
с
оно разрушается, переходя в строго
равновесное состояние.
с
до
с
после смены направления магнитного
поля может рассматриваться как
находящаяся в состоянии статистического
равновесия. Строго говоря, состояние
спиновой системы с ориентацией против
магнитного поля неравновесно и через
с
оно разрушается, переходя в строго
равновесное состояние.
Термодинамическая вероятность состояний, при котором спинов ориентированы по полю, а – против равна
 .
.
В соответствии с формулой Больцмана энтропия при этом будет составлять
 ,
,
или
учитывая, что по теореме Стирлинга
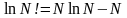 ,
формулу Больцмана можно свести к виду
,
формулу Больцмана можно свести к виду
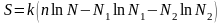 .
.
Абсолютная
температура системы равна частной
производной
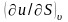 ,
тогда
,
тогда
 .
.
При
 выполняется условие
выполняется условие
 ,
а в случае
,
а в случае
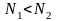 абсолютная температура окажется
отрицательной, то есть
.
Это позволяет сделать следующий вывод
относительно состояний с отрицательной
абсолютной температурой.
абсолютная температура окажется
отрицательной, то есть
.
Это позволяет сделать следующий вывод
относительно состояний с отрицательной
абсолютной температурой.
Такие состояния могут иметь место лишь в системах, у которых внутренняя энергия и не может принимать значений, больших некоторой конечной величины Uа и меньше некоторой конечной величины U0.
 .
.
Таким образом, рассмотренное выше состояние ядерных спинов некоторых парамагнитных материалов во внешнем магнитном поле, когда спины в основном ориентированы против магнитного поля, представляют собой неравновесное в целом (но метастабильное или квазиравновесное по отношению к достаточно малому промежутку времени) состояние с отрицательной температурой, а с ориентацией по полю – равновесное состояние с положительной температурой.
На
основании вышеизложенного можно сделать
вывод о том, что состояния при
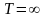 и
и
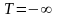 тождественны, ибо соответствуют одним
и тем же значениям
тождественны, ибо соответствуют одним
и тем же значениям
 и
и
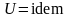 .
.
В
то же время состояния при
и
 приводят к различным значениям внутренней
энергии
приводят к различным значениям внутренней
энергии
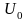 и
и
 ,
а значит существенно отличны друг от
друга при одинаковых значениях
,
а значит существенно отличны друг от
друга при одинаковых значениях
 и
и
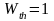 (так как при этом
(так как при этом
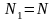 или
или
 ).
Непрерывный переход между этими
состояниями невозможен.
).
Непрерывный переход между этими
состояниями невозможен.
