6 Второе начало и необратимость процессов

ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ

6.1 Необратимость теплообмена

Рис. 6.1 К выводу необратимости теплообмена

Пусть газ помещен в сосуд с адиабатными стенками, разделенный на две части диатермической перегородкой. Все координаты, определяющие производство работы в подсистемах, например, объёмы остаются постоянными: , . Системы гомогенны , , но . Диатермическая перегородка допускает обмен теплом, но при этом будем считать, что гомогенность и равновесность каждой из подсистем остаются неизменными. Это позволяет предположить, что процессы изменения внутренней энергии в каждой из подсистем будут протекать обратимо. Но в целом в адиабатной системе процесс теплообмена необратим. Покажем это.

По отношению к каждой из подсистем такая необратимость носит внешний характер. Запишем первое начало термодинамики для процессов, протекающих в подсистемах «А» и «В»: , ; , . Но при этом внутренняя энергия полной адиабатной системы остается неизменной

,

откуда следует , а это возможно, если выполняется следующее равенство по бесконечно малым тепловым эффектам

. (6.1)

Найдем соответствующее тепловым эффектам изменение энтропии в каждой из подсистем «А» и «В»

;. .

Тепло и измененные энтропии определяются по обратимым процессам, протекающим в соответствии с принятыми допущениями в каждой из подсистем.

Энтропия системы в целом должна возрасти, так как в ней протекает необратимый процесс. Приращение энтропии системы найдем как сумму

изменения энтропии в подсистемах «А» и «В».

. (6.2)

тепло переходит от В к А, следовательно .

Приращения энтропии 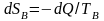; , но так как , то

. (6.3)

Рис. 6.2 Необратимость теплообмена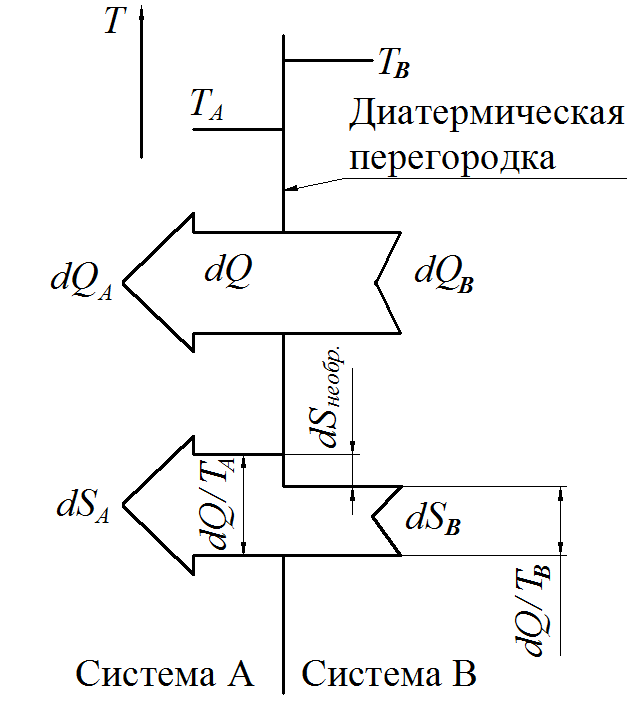

Таким образом, можно сделать вывод о том, что энтропия системы, воспринимающей тепло, возрастает больше, чем убывает энтропия системы, отдающей его. Следовательно, энтропия полной системы в рассмотренном примере в соответствии со вторым законом термодинамики возрастает :

. (6.4)

Иногда для иллюстрации необратимости теплообмена применяют энтропийные диаграммы (рис. 6.2)

Теплообмен связан с переносом энергии. Очевидно, что перенос энергии приводит к переносу энтропии в том же направлении. Можно отметить, что в диатермической перегородке, где проявляется скачок температуры, осуществляется производство энтропии, величина которого может быть рассчитана по выражению

. (6.5)

Произведенная энтропия увеличивает энтропию, поступающую от системы В, так, что система А воспринимает энтропию величиной

. (6.6)

Необратимость процесса может оцениваться величиной произведённой энтропии.

Энергию, передаваемую в форме тепла, за бесконечно малое время можно найти из дифференциального выражения

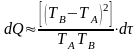. (6.7)

6.2 Перенос и производство энтропии

Система, воспринимающая или отдающая энергию в форме тепла, соответственно, получает или отдает энтропию величиной

.

Подвод тепла увеличивает, а отвод уменьшает энтропию системы. Через границы адиабатной системы тепло и, следовательно, энтропия не передаются. При обратимом процессе изменение энтропии системы совпадает

.

Энтропия может не только переноситься через границы системы, но и непосредственно производиться в ней вследствие протекающих необратимых процессов. Это либо диссипативные процессы, либо процессы, связанные с выравниванием параметров состояния по объёму системы. Уменьшение энтропии изолированной адиабатной системы по второму началу невозможно.

В связи с этим для неадиабатных систем целесообразно разделение изменения энтропии на две части:

, – энтропия, перенесённая с теплом через границы системы, знак которой определяется; подводится (+) или отводится (–) тепло. Что касается энтропии, произведению в системе, то она определяется неравенством

– энтропия, произведенная в системе.

Равенство возможно лишь при протекающих полностью обратимо процессах.

Тогда для второго начала термодинамики можно дать следующую формулировку:

Изменение энтропии закрытой системы состоит из двух частей – из энтропии, перенесённой с теплом через её границы, и из энтропии, произведенной в системе

.

Произведенная энтропия всегда больше либо равна нулю, то есть она не может быть отрицательной

,

Это означает, что для ограниченных систем уничтожение энтропии невозможно.

В отличие от энтропии системы, перенесённая и произведенная энтропии являются параметрами состояния, а относятся к функциям процесса. Поэтому в уравнении

(6.8)

энтропию, произведенную в процессе , можно рассматривать как количественную меру его необратимости.

6.3 Диссипация энергии

При протекании в системе обратимого процесса энергия, переходящая через границу в форме тепла, равна

, (6.9)

а энергия, передаваемая в форме работы, – по изменению обобщенных координат , рассчитывается по очевидной зависимости

. (6.10)

Тепло и работа, исходя из объединенного уравнения первого и второго начал термодинамики, соответствуют отдельным слагаемым дифференциала внутренней энергии

. (6.11)

При необратимых процессах изменение энтропии происходит как вследствие её переноса, так и из-за её производства

, (6.12)

где – произведённая энтропия.

Если теплообмен отсутствует между частями системы, то есть внутри системы, то производство энтропии происходит из-за наличия диссипации: трение, тепловыделение в проводнике при прохождении электрического тока, работа вала и так далее.

Рис. 6.3 Адиабатные системы с подводом энергии в форме работы

и изменения обобщенных координат

Рассмотрим две адиабатные системы (рис. 6.3).

Системы адиабатны . Обобщенная координата в виде объема в схемах остается неизменной . Тогда в соответствии с первым началом термодинамики изменение внутренней энеогии в них может произойти за счет механической энергии в первом случае и за счет выделения Джоулевого тепла на омическом сопротивлении во втором.

Для них первое начало может быть записано в виде . В первой системе обобщенная координата – объём, во второй – объём и электрический заряд.

где dQ_э – элементарное изменение электрического разряда.

Тогда для производства энтропии можно записать

_(6.13)

где dQ_э – элементарный электрический заряд системы; dQ_эт – элементарный электрический заряд, протекающий по резистору с электрическим сопротивлением R.

Они при производстве работы остаются постоянными ,

,

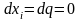где – элементарнее изменение электрического разряда.

Энергия, подводимая в форме работы при постоянных или даже отсутствующих обобщенных координата, приводит к увеличению внутренней энергии в процессе производства энтропии.

Необратимый процесс, при котором энергия, подводимая в форме работы, воспринимается системой без изменения обобщенных координат или , называется диссипативным (диссипация работы).

Количественно диссипирующая энергия может быть рассчитана по выражению

.

Тогда для приведенных примеров

,

то есть подводимая работа полностью диссипирует.

С учетом диссипирующей энергии уравнение для расчета приращения энтропии примет вид

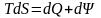. (6.14)

Для конечного необратимого процесса при квазистатических изменениях состояния системы после интегрирования получим

. (6.15)

Для адиабатной системы , и

(6.16)

Таким образом, площадь под кривой, изображающей в – диаграмме реальную адиабату, равна энергии диссипации (рис. 6.4). В случае простой системы с объёмом как единственной обобщённой координаты можно записать соотношение

Рис. 6.4 Диссипация в необратимом

адиабатном процессе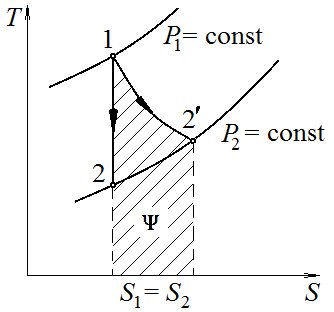

.

Откуда для работы при адиабатно протекающих процессах можно получить

и для работы в целом за процесс изменения от состояния «1» до состояния «2»

. (6.17)