3 Газовые смеси

Практически во всех сферах деятельности мы сталкиваемся не с веществами в чистом виде, а с их химическими соединениями, либо с механически перемешенными веществами или растворами. К примеру, рабочие тела почти всех тепловых машин представляют собой некоторую газовую смесь. Не составляет исключение и воздух, которым мы дышим и используем в большинстве случаев как окислитель в камерах сгорания двигателей, топках различных топливосжигающих устройств. Как известно, воздух состоит из 78,08 % азота N₂, 20,95 % кислорода О₂ и где-то около 1 % составляют примеси других газов. С экологической точки зрения хотелось бы, чтобы процент примесей не возрастал в результате не всегда разумного вмешательства человечества в естественные массообменные процессы природы.

При термодинамических расчетах рабочих процессов тепловых машин мы сталкиваемся с необходимостью определения термодинамических параметров рабочих тел, в подавляющем большинстве случаев представляющих собой газовую смесь продуктов сгорания углеводородных топлив, что требует умения и навыков расчета газовых смесей. Следовательно, должны быть разработаны методы их расчета и способы задания газовых смесей.

3.1 Способы задания газовой смеси

Под смесью идеальных газов понимается механическая смесь химически обособленных исходных газов, подчиняющихся уравнению состояния идеального газа. Тогда будем считать, что и смесь представляет из себя некоторый самостоятельный идеальный газ, термодинамические свойства которого определяются количественным соотношением входящих в него исходных компонентов, то есть свойства газовой смеси однозначно определяются ее составом.

Состав газовой смеси определяется количественным соотношением входящих в него компонентов и может быть задан массовыми, объемными или мольными долями.

Пусть М_см – масса газовой смеси, а т_i – масса i-го компонента, входящего в смесь. Согласно закону сохранения массы будем иметь очевидное равенство:

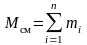, (3.1)

где n – число компонентов смеси.

Под массовой долей i-го компонента будем понимать отношение:

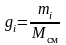или в процентах 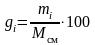 %. (3.2)

На основании закона сохранения вещества, запишем уравнение баланса массы:

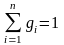. (3.3)

Если массовые доли заданы в процентах, то

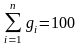 %. (3.4)

Объемные доли представляют собой отношение парциальных объемов компонентов к объему газовой смеси:

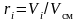, (3.5)

где V_i – парциальный объем i-го компонента; V_см – объем газовой смеси.

Под парциальным объемом будем понимать тот объем, которым бы обладал i-й компонент, находясь при температуре 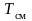и давлении 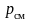газовой смеси.

Нетрудно показать, что парциальные объемы газов прямо пропорциональны их парциальным давлениям. Парциальным называется давление, которое создавал бы i-й газ смеси, если бы он один занимал весь объем смеси, находясь в нем при температуре смеси.

Запишем уравнение Бойля-Мариотта для компонента смеси:

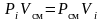, то есть (3.6)

,

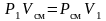или

, ,

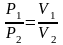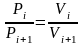где P_i – парциальное давление i-го компонента; V_i – парциальный объем i-го компонента.

Сложим почленно левые и правые части закона Бойля-Мариотта для компонентов:

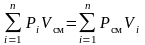или .

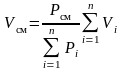Согласно закону Дальтона

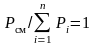, (3.7)

тогда 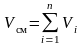. (3.8)

Объем газовой смеси равен сумме парциальных объемов компонентов, входящих в смесь. Это утверждение равносильно равенству

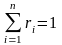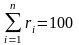или  %. (3.9)

Состав газовой смеси может быть задан и числом молей, входящих в нее компонентов

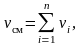(3.10)

где 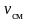– число молей смеси; 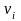– число молей i-го компонента.

Тогда под мольной долей будем понимать отношение

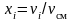(3.11)

и, согласно закону сохранения количества вещества, будем иметь равенство

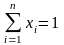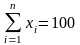или  %. (3.12)

Воспользуемся следствием из закона Авогадро: одинаковые количества различных идеальных газов, находящихся при одинаковых давлениях и температуре, занимают одинаковые объемы.

Запишем 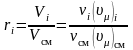, но ,

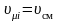тогда 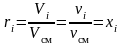, (3.13)

то есть объемные и мольные доли компонентов смеси равны между собой.

3.2 Термическое уравнение состояния газовой смеси

Запишем уравнение состояния для i-го компонента газовой смеси, если он занимает весь ее объем и находится там при температуре смеси. Тогда его давление равно парциальному:

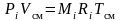. (3.14)

Просуммируем полученные зависимости для всех компонентов, входящих в смесь

.

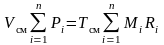Вспоминая, что 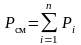и, вводя обозначение ,

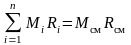получим уравнение состояния газовой смеси:

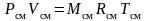, (3.15)

где R_см – газовая постоянная смеси. Ее величина может быть рассчитана из соотношения

.

Поделив его на массу смеси М, получим соотношение:

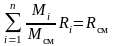, но ,

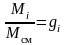тогда 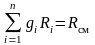. (3.16)

Введение понятия о кажущейся молекулярной массе смеси упрощает расчеты газовых смесей:

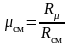. (3.17)

Или после подстановки выражения (3.17) для 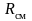получим с учетом равенства 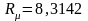 Дж/(моль∙К)

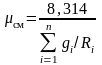. (3.18)

Запишем уравнение состояния для массы газа m_i:

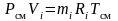или, с учетом ;

.

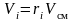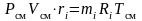Последнее выражение преобразуем к виду

.

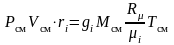Если записать выражения для каждого компонента смеси, а затем просуммировать, получим

; ,

тогда .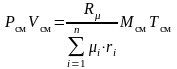

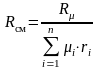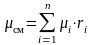Таким образом , а . (3.19)

Получим расчетные зависимости для и 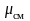, если смесь задана массовыми долями 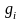. Запишем уравнение состояния для М кг газовой смеси и для 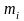 кг компонентов газов, входящих в смесь, через их парциальные объемы:

; .

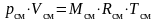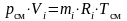Если записать второе выражение для каждого компонента, а затем их просуммировать, то получим

.

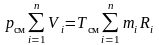Перепишем его в виде .

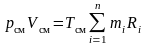Поделив последнюю зависимость на уравнение состояния смеси для М кг, получим зависимость для расчета R_см и _см через массовый состав:

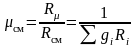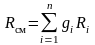; . (3.20)

Последние выражения позволяют по объемным долям и молекулярным массам компонентов рассчитать газовую постоянную смеси и среднюю молекулярную массу.

Зная соотношения между массовыми и объемными долями газов, можно рассчитать парциальные давления

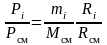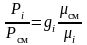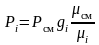; или . (3.21)

Запишем закон Бойля-Мариотта для i-го компонента и всей смеси

,

откуда ,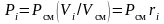

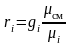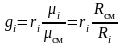тогда или . (3.22)

Приравнивая зависимости (3.21) и (3.22), получим формулы перевода массовых долей в объемные и наоборот:

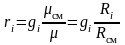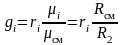; . (3.23)

Плотность газовой смеси:

,

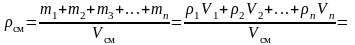
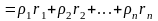таким образом, 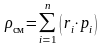. (3.24)

Выразим 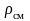через массовый состав смеси:

,

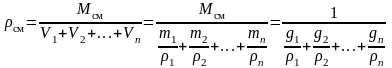следовательно, .

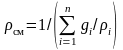3.3 Теплоемкость смеси газов

Пусть известны c_i – зависимость массовых теплоемкостей компонентов от температуры

.

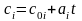Для одного килограмма газовой смеси массовая теплоемкость может быть рассчитана по формуле

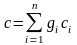. (3.25)

Или с учетом зависимости теплоемкостей от температуры

.

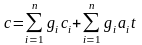Если задан объемный состав, то удобней пользоваться объемными теплоемкостями:

для 1 м³ компоненты: ,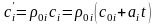

для 1 м³ смеси: 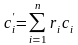. (3.26)

Или с учетом зависимости от температуры:

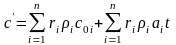. (3.27)

3.4 Энтропия газовой смеси

Воспользовавшись объединенным выражением первого и второго начал термодинамики, запишем

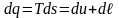
или

.

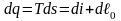Распишем выражения, входящие в правые части

; ; ; .

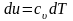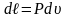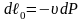Тогда после подстановки получим

; .

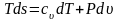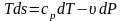Предполагая газ совершенным, а следовательно, подчиняющимся уравнению состояния в форме Клапейрона-Менделеева, преобразуем, правые части к виду, удобному для интегрирования (исключим лишнюю переменную)

; .

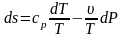Запишем уравнение состояния и выразим из него давление и удельный объем

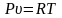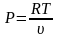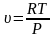; ; или ; .

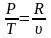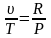После подстановки в (3.26) и (3.27)

; .

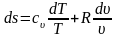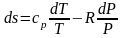Проинтегрируем (3.26) и (3.27) от состояния 1 до состояния 2:

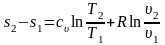; (3.28)

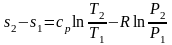. (3.29)

Если в качестве независимых переменных будут выбраны 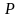и , то выражение для расчета изменения энтропии в политропных процессах может быть преобразовано к виду

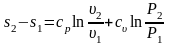. (3.30)

Известно, что энтропия является аддитивной функцией состояния, а, следовательно, для системы, состоящей из «n» частей, должны вычисляться соотношения

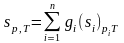. (3.31)

С другой стороны энтропия может быть рассчитана по зависимости, в которой в явной форме аддитивность не отражена

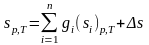. (3.32)

По своей сути выражения (3.32) и (3.31) эквивалентны.

Энтропия смеси идеальных газов представляет собой сумму энтропий газов, входящих в смесь

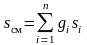. (3.33)

Для газа с параметрам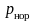и и 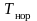следует, что его энтропия в соответствии с (3.29) равна

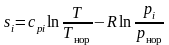, (3.34)

где – температура нормиро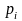вки; – парциальное давление; – давление нормировки.

Парциальное давление компонента в смеси можно определить по ранее приведенной зависимости

.

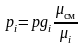Тогда второе слагаемое правой части выражения (3.34) может быть сведено к виду

.

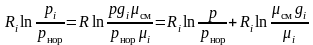Следовательно, выражение для энтропии газовой смеси (3.33), представленное в виде аналогичном (1.31), можно переписать

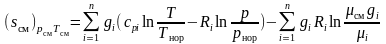. (3.35)

Выражение, стоящее в скобках в правой части (3.35), представляет собой энтропию 1 кг компонента при параметрах смеси, которую можно обозначить, как 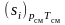, а последнюю сумму можно определить как приращение энтропии в процессе необратимого смешения идеальных газов, входящих в смесь. Так как по смыслу величина 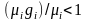, то выражение (1.35) может быть переписано в виде

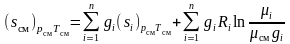. (3.36)

Учитывая формулу соотношения массовых и объемных долей 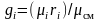, перепишем (3.36)

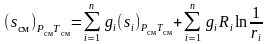. (3.37)

Из (3.37) следует, что смешение различных газов при 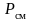, приводит к возрастанию энтропии на величину энтропии смешения

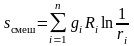(3.38)

или для отдельно взятого i-го компонента

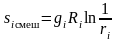. (3.39)

Выражение (3.32) учитывает возрастание энтропии i-го компонента за счет необратимости процесса смешения.