1.4. Решение контрольной задачи для одного шага интегрирования методами Эйлера и Рунге-Кутта (Проведение расчетов без пк).

1.4.1. Начальные условия.

Для решения тестового примера на 1 шаг интегрирования системы (1.1) методами Эйлера и Рунге- Кутта задаем следующие начальные условия:

1.Шаг интегрирования h принимаем равным 0.05 секунды (h=0.05 сек.);

2. V=V_g, где V_g- скорость ЛА в момент схода с направляющих, рассчитываемая по формуле:

, где

_g- угол наклона направляющих; _g=45⁰=0,785 рад;

t_g- дульное время, рассчитываемые по формуле:

V_g = и t_g = , где

=

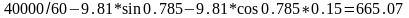
V_g =

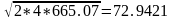
3. _g- угол наклона направляющих; _g=45⁰=0,785 рад.

4. х- начальная абсцисса, рассчитываемая по формуле:

х=S_n*cos_g=4*0.785=3.96 м

5. у- начальная ордината, рассчитываемая по формуле:

у= S_n*sin_g=4*0.785=3.96 м

1.4.2. Расчет системы уравнений методом Эйлера (1 шаг).

1. Нахождение коэффициентов к1 для каждого уравнения.

По определению коэффициенты К1- это правые части уравнений, вычисленные при начальных условиях.

а. плотность при начальной высоте :

б. лобовое сопротивление при начальной (дульной) скорости:

X=0,5*0.26*0.01767*1.22967*(72.9421)²=15.0288

в. Масса при начальном (дульном) времени:

m=60-20*0.1095=57.81

г. К1(1)= (40000 - 9.81*57.81* 0.785 - 15.0288) / 57.81 = 683.96 м/с²

К1(2)=-9,81*cos45⁰/ 22,708= -0.7761 рад/с

К1(3)=22,708*cos45⁰= 3.51304 м/с

К1(4)=22,708*sin45⁰= 3.4857 м/с

2. Результаты одного шага интегрирования по методу Эйлера:

V=V_g+К1(1)*h = 72.9421+683.96*0.05 = 107.13 м/с

_g+К1(2)*h = 0.785+(-0.7761)*0.05 = 0.76867 рад

x=x₀+К1(3)*h=3.96 + 3.51304*0.05=2.82 м

y=y₀+K1(4)*h=3.96 + 3.4857* 0.05=2.82 м

1.4.3. Расчет системы уравнений методом Рунге-Кутта (1 шаг).

1. Нахождение коэффициентов к1 для каждого уравнения.

По определению коэффициенты К1- это правые части уравнений, вычисленные при начальных условиях.

а. плотность при начальной высоте :

б. лобовое сопротивление при начальной (дульной) скорости:

X=0,5*0.26*0.01767*1.22967*(72.9421)²=15.0288

в. Масса при начальном (дульном) времени:

m=60-20*0.1095=57.81

г. К1(1)= 8,1224487289

К1(2)= -0,0112446838

К1(3)= 1,091383734

К1(4)= 1,0905149817

2. Нахождение коэффициентов К2 для каждого уравнения.

По определению коэффициенты К2- это правые части уравнений, вычисленные при полученных новых значениях параметров.

К2(1)= 8,1419713966

К2(2)= -0,009992507

К2(3)= 1,241945517

К2(4)= 1,2270805529

3. Нахождение коэффициентов К3 для каждого уравнения

По определению К3- это правые части уравнений, вычисленные при полученных новых значениях параметров.

К3(1)= 8,1417519898

К3(2)= -0,0099835329

К3(3)= 1,2415239848

К3(4)= 1,2282011286

4. Нахождение коэффициента К4 для всех уравнений

По определению К4- это правые части уравнений, вычисленные в конце шага

К4(1)= 8,1610849832

К4(2)= -0,0089854278

К4(3)= 1,3930436092

К4(4)= 1,364415478

5. Результаты одного шага по методу Рунге- Кутта.

V=V_g+(1/6)*(K1(1)+K4(1)+2*(K2(1)+K3(1))) = 30.85671 + (1/6)*( 8,1224487289+

+ 1,0905149817+2*( 1,091383734 -0,0112446838)) = 38,9985400808;

_g+(1/6)*(K1(2)+K4(2)+2*(K2(2)+K3(2))) = 0.78539 + (1/6)*( 8,1419713966+

+1,2270805529+2*( 1,241945517 -0,009992507)) = 0,7749696348;

x=x_g+(1/6)*(K1(3)+K4(3)+2*(K2(3)+K3(3))) = 2.121 + (1/6)*( 8,1417519898+

+ 1,2282011286+2*( 1,2415239848-0,0099835329)) = 3,3640591986;

у=у_g+(1/6)*(K1(4)+K4(4)+2*(K2(4)+K3(4))) = 2.121 + (1/6)*( 8,1610849832+

+ 1,364415478+2*( 1,3930436092 -0,0089854278)) = 3,3480578471;