Балтийский Государственный Технический Университет им. Д.Ф. Устинова. (ВОЕНМЕХ)

Кафедра А5

Курсовой проект:

«Проект компьютеризации расчета траектории неуправляемого летательного аппарата»

Выполнил: Смирнов А. В.

Группа: А-531

Проверил: Шалыгин А. С.

Санкт-Петербург

2005г.

Содержание

Исходные данные и полученные результаты

1. Постановка задач. Анализ и представление исходных данных.

2. Модель динамики неуправляемого ЛА.

   1. Движение ЛА по направляющим.

   2. Активный участок полета ЛА.

   3. Пассивный участок полета ЛА.

3. Алгоритмы численного интегрирования методов Эйлера и Рунге-Кутта.

4. Решение контрольной задачи для одного шага интегрирования методами Эйлера и Рунге-Кутта (Проведение расчетов без ПК).

5. Результаты расчетов траекторных параметров неуправляемого ЛА.

6. Расчет траектории пассивного участка с использованием параболической теории.

Приложение 1. Графики V(t), θ(t), y(x) методами численного интегрирования и по параболической теории).

Приложение 2. Текст программы, разработанной для интегрирования методами Эйлера и Рунге-Кутта.

Список литературы.

Исходные данные и полученные результаты:

Калибр d, м	Полный вес G, кг	Вес топлива , кг	Время горения топлива t,с	Длина направляющих Sн, м	Коэффициент i	Угол подъема направляющих , 0	Эффективная скорость истечения Ue, м/с
0.15	60	12	0.6	4	1.6	45	2000

Дополнительные параметры

Секундный массовый расход Q, кг/с	Тяга R, кг*м/с2	Коэффициент лобового сопротивления Cx	Площадь миделя S, м2
20	40000	0.26	0.01767

Движение по направляющим

Дульная скорость Vd, м/с	Дульное время td, с	Угол наклона d, град
39.514	0.19445	45

Активный участок траектории ЛА

Обозначение	Va ,м/с	ta, c	a , рад	Xa , m	Ya, m	M, kg
Метод Эйлера	356,305	2	0,687	274,737	234,633	100
Метод Р-К	357,048	2	0,681	270,014	228,664	100

Пассивный участок траектории ла.

Обозначение	Vp,м/с	tp,c	p,рад	Xp,m	Yp,m
Метод Эйлера	46,05	285,498	-0,813	10503,017	0
Метод Р-К	45,9	286,014	-0,808	10534,668	0

Глава 1

1.Разработка Компьютерной модели расчета траектории неуправляемого летательного аппарата.

1.1 Постановка задач. Анализ и представление исходных данных.

В этой главе рассмотрены следующие задачи:

1. Разработка компьютерной модели расчета траектории неуправляемого ЛА, используя методы численного интегрирования Эйлера и Рунге-Кутта.

2. Расчет траектории пассивного участка полета неуправляемого ЛА с использованием параболической теории.

Траектория полета неуправляемого ЛА (снаряда РСЗО) состоит из трех характерных участков:

1. движение по направляющим;

2. активный участок;

3. пассивный участок.

Расчет дополнительных параметров:

1. Секундный массовый расход (q) рассчитан по формуле:

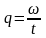
2. Тяга двигателя (R) рассчитана по формуле:

R=U_e*q

3. Коэффициент лобового сопротивления рассчитан по формуле:

C_x=C_x(M)*i , где C_x=C_x(M)-коэффициент лобового сопротивления эталонного ЛА. Принимаем C_x =0.3.

4. Площадь миделя ЛА рассчитана по формуле:

5. Закон изменения массовой плотности воздуха от высоты полета принимаем в виде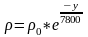 , где r_o= 1.23- плотность воздуха на уровне моря; высота y в формуле берется в метрах.

6. Закон изменения массы принимаем в виде m= m₀-q*t.

1.2. Модель динамики неуправляемого ла.

1.2.1. Движение ла по направляющим.

При расчете движения по направляющем принимается во внимание действие на ЛА следующих сил: R- тяга, G- вес ЛА, F- реакция направляющих, которая состоит из силы трения Fтр и нормальной составляющей N. Аэродинамическими силами при расчете движения по направляющим обычно пренебрегают.

Кроме того, в идеальном случае направляющие принимаются жесткими и недеформированными. Расчетная схема движения представлена на рисунке 1.1.

Рис 1.1.

Уравнение движения ЛА на направляющих в проекции на направление скорости запишется в виде

где f- коэффициент трения скольжения, m=m₀-Q*t – принимаемый в работе закон изменения массы ЛА, G=m*g. Записывая уравнение движения в нормальной форме Коши, получаем

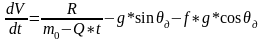
Последовательно интегрируя уравнение с учетом соотношения ds/dt=v, находим

Полагая в формулах t=td, получаем выражение для дульной скорости Vd и длины направляющих:

Если задана длина направляющих Sh, то, решая численно уравнение, определим td. Для этого уравнение запишем в виде

Если пренебречь изменением массы при движении ЛА по направляющим, то, заменяя массу ЛА средним значением m= mср, получаем

По этим формулам можно приближенно найти vd и td.

Примечание: 1. Коэффициент трения скольжения ЛА об направляющие f равен 0.15 (f=0.15).

2. Изменением массы при движении ЛА по направляющим пренебрегаем.

1.2.2. Активный участок полета ла.

При расчете активного участка полета ЛА принимают следующие допущения:

1. угол атаки равен нулю.

2. тяга R постоянна.

При сделанных допущениях уравнения для расчета траектории ЛА на активном участке полета запишутся в виде следующей системы дифференциальных уравнений первого порядка:

(1.1)

Здесь X=0.5*Cx*Ro*S*V – сила лобового сопротивления. Остальные элементы системы были указаны выше.