69. Отображения множеств. Функция. Биекция.

Для решения вопроса о том, равное ли число элементов содержат два множества A и B, можно поступить двумя способами. Первый способ состоит в подсчёте числа элементов в каждом множестве и сравнении полученных натуральных чисел. Второй способ не требует знания количества элементов в каждом из множеств А и В. Он состоит в попытке установить между множествами А и B взаимно однозначное соответствие (биекцию). Если биекцию f:А→ B удалось отыскать, то это означает, что количество элементов в А и B одинаково. Например, если в трамвае каждый пассажир сидит на сидении , и при этом нет ни свободных мест, ни стоящих пассажиров, то тем самым установлено взаимно однозначное соответствие (биекция) между множеством пассажиров и множеством посадочных мест, поэтому число сидений в данном трамвае равно числу севших в него пассажиров. Хотя второй метод несёт меньше информации, чем первый (он устанавливает равенство числа элементов в множествах А и B, но не указывает самого числа), у него есть преимущество применимости для количественного сравнения бесконечных множеств.

Определение: Множество A называется эквивалентным множеству B, если существует биекция f:А→B. В этом случае говорят также, что множество A имеет одинаковую мощность с множеством B. Обозначение:A~B или  .

Примеры

1. Множество всех натуральных чисел 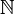  эквивалентно множеству 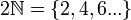  всех чётных чисел, так как отображение 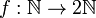 , определяемое формулой f(n)=2n есть биекция.

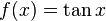2. Функция   взаимно однозначно отображает интервал   на все множество действительных чисел  . Поэтому 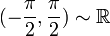 . (Заметим: оказывается, в ограниченном интервале содержится столько же точек, сколько и на всей бесконечной числовой прямой!)

3. Функция f=(b-a)x+a взаимно однозначно отображает интервал (0,1) на интервал (a,b), а сегмент [0,1] на сегмент [a,b], поэтому (0,1)~(a,b); [0,1]~[a,b].

Теорема 1:

1. Всегда A~A;

2. Если A~B, то B~A.

3. Если A~B и B~C, то A~C.

Доказательство строится на определении эквивалентного множества и свойств биекции:

1. Тождественное отображение id:A→A есть биекция.

2. Если f:А→B- биекция, то и обратное отображение f^-1:B→A— биекция.

3. Если f:A→B и g:B→C- биекции, то и их композиция f•g:A→C - биекция.

Теорема 2: Если A₁~B₁, A₂~B₂,то  .

Доказательство

Пусть f₁:A₁→B₁ и f₂:A₂→B₂- биекции. Определим отображение   формулой f(a₁,a₂)=(f₁(a₁), f₂(a₂)). Тогда f есть биекция, так как для любого элемента (b₁, b₂) декартова произведения   в декартовом произведении   имеется единственный прообраз относительно отображения f, именно точка  .

Tеорема 3: Пусть   и  - два семейcтва попарно непересекающихся множеств, и пусть существует такая биекция: f:X→Y, что A_x~B_f(x) для любого элемента  . Тогда множества   и   эквивалентны.

Доказательство

Обозначим через g_x биекцию множества А_x на множество B_f(x). Пусть  - произвольный элемент из А. Тогда, так как множества первого семейства попарно не пересекаются, существует единственный элемент  , такой, что  . Поставим в соответствие элементу a элемент g_x(a) из B_f(x), принадлежащий вместе с тем и множеству B. Получим биекцию множества А на B. Действительно, если b произвольный элемент из B, то в силу попарной непересекаемости множеств второго семейства, существует единственный элемент  , такой, что  . Ясно, что элемент   является единственным прообразом элемента b при нашем соответствии.

Tеорема 4: Если   и A₃~A₁, то A₂~A₁.

Доказательство

Так как A₁~A₃, то существует биекция f:A₁→A₃. Положим   и далее по индукции, если множества A₁, A₂,...A_n уже определены, то полагаем  . Таким образом, получается последовательность множеств  . Покажем, что эта последовательность удовлетворяет следующим трем условиям:

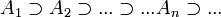1.   (1)

2. для всех m≠n    (2)

3. для всех    (3)

Докажем условие (1) по индукции. Отношения   выполнены по условию теоремы. Допустим, что верны отношения  . Тогда из   следует  , то есть  . Тем самым условие (1) доказано. Условие (2) вытекает из (1), так как при m≠n полагая, например, m>n, будем иметь  . Следовательно, любая точка из A_m\A_m+1 не принадлежитA_n\A_n+1. Для доказательства (3) заметим, что из отношений   и биективности f следует  , что и означает справедливость отношений (3).

Положим  . Тогда справедливы равенства (4):     и (5):   , причём слагаемые в них попарно не пересекаются. Докажем, например, равенство (4). Из соотношений (1) следует, что все слагаемые правой части равенства (4) содержатся в его левой части. Докажем обратное включение. Пусть  . Если  , то   принадлежит и всей правой части. Если же  , то существует такоЙ номер n, что  . Пусть m - наименьший из номеров, для которого  . Так как  , то m ≥ 2. Ясно, что  . Поэтому  . Следовательно,   принадлежит и всей правой части равенства (4), что и завершает его доказательство.

Докажем еще, что слагаемые в правой части равенства (4) попарно не пересекаются. Первое слагаемое С не пересекается с любым слагаемым   в силу очевидного включения  , а остальные слагаемые попарно не пересекаются в силу (2).

Если положить  , то равенства (4) и (5) можно переписать следующим образом: . В этих двух объединениях слагаемые, стоящие на одинаковых местах, начиная со второго, эквивалентны в силу (3), а первые слагаемые одинаковы и потому тоже эквивалентны. По теореме 3: множества A₁ и A₂ эквивалентны.

Понятие эквивалентности двух множеств было бы бессодержательным, если б оказалось, что все бесконечные множества эквивалентны между собой. Однако это не так, что и вытекает из следyщей теоремы.

Теорема 5 (Теорема Кантора):. Множество X и его булеан (множество всех его подмножеств)   не эквивалентны.

Доказательство

Допустим противное, что  . Тогда существует биекция:  . Для любого элемента    f(x) есть элемент булеана  , то есть подмножество множества X. Возможны две ситуации: либо  , либо  . Обозначим через Y множество всех таких элементов  , что  . Множество Yодновременнно является элементом булеана  . Поэтому существует такой единственный элемент   , что f(y₀)=Y. Ясно, что либо  , либо  . Покажем, что оба эти отношения невозможны, что и докажет теорему.

Пусть  . Но Y=f(y₀), значит  . Но в таком случае по определению Y  . Получили противоречие. Пусть теперь  . Но такой элемент должен по определению множества Y принадлежать Y:  . Опять получилось противоречие.