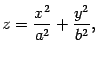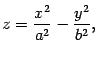68. Эллиптический и гиперболический параболоиды.

Определение 13.7   Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

(13.13)

где   и   -- положительные числа.         

Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости   ,   и координатная ось   .

Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью   . На этой плоскости   , поэтому

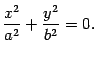
Координаты только одной точки плоскости   могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью   . На этой плоскости   , поэтому

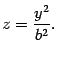
Это уравнение параболы на плоскости   . Построим ее (рис. 13.19). Сечение плоскостью   также является параболой. Нарисуем и ее (рис. 13.19). Найдем линии пересечения поверхности с плоскостью   . Уравнения этой линии

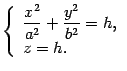
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если   . Эта точка называется вершиной параболоида.

Пусть   . Первое уравнение преобразуем к виду

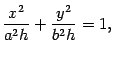
то есть к виду

(13.14)

где   ,   . Уравнение (13.14) является уравнением эллипса. Нарисуем полученное сечение (рис. 13.19). При   плоскость поверхность не пересекает.

Рис.13.19.Сечения эллиптического параболоида координатными плоскостями

Найдем сечения параболоида плоскостями   , параллельными плоскости   . Линии этих сечений удовлетворяют уравнениям

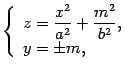
и являются параболами, такими же, как в плоскости   , только сдвинутыми вверх на величину   , их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью   (рис. 13.20).

Рис.13.20.Дополнительные сечения параболоида

Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости   . Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости   , а вершина скользила по параболе в плоскости   .

Привычное для глаза изображение приведено на рисунке 13.21.

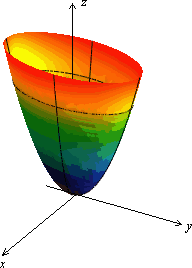
Рис.13.21.Эллиптический параболоид

Если в уравнении (13.13)   , то сечения плоскостями, параллельными плоскости   , являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости   , вокруг оси   (рис. 13.22).

Рис.13.22.Параболоид вращения

        Определение 13.8   Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

(13.15)

где   и   -- положительные числа.         

Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости   ,  и координатная ось   .

Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью   . На этой плоскости   , поэтому

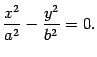
Это уравнение определяет на плоскости   пару прямых   , изображенных на рисунке 13.23.

Найдем линию пересечения с плоскостью   . На этой плоскости   , поэтому

Это уравнение на плоскости   задает параболу, ветви которой направлены вниз. Построим ее (рис. 13.23). Сечение плоскостью   также является параболой

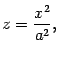
но ее ветви направлены вверх. Нарисуем и ее (рис. 13.23).

Рис.13.23.Сечения гиперболического параболоида координатными плоскостями

Найдем линии пересечения поверхности с плоскостью   ,   . Уравнения этой линии

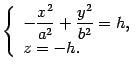
Первое уравнение преобразуем к виду

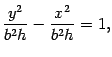
то есть к виду

(13.16)

где   ,   . Уравнение (13.16) является уравнением гиперболы. Ее действительная ось параллельна оси   , а мнимая -- оси   . Полуоси равны соответственно   и   . Нарисуем полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 13.24).

Найдем линии пересечения с плоскостями   , параллельными плоскости   . Уравнения этих линий

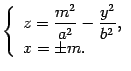
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью   , только сдвинутой вдоль оси   на величину  вверх. Эти параболы изображены на рисунке 13.24.

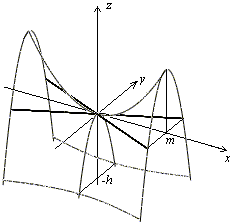
Рис.13.24.Изображение гиперболического параболоида с помощью сечений

Так как   -- произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости   . Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости   , а вершина скользила по параболе в плоскости   .

Плоскость   ,   , пересекает поверхность по гиперболе, но в отличие от гиперболы (13.16), ее действительная ось параллельна теперь оси   , а мнимая -- оси   (рис. 13.25).

Рис.13.25.Дополнительное сечение

Привычное для глаза изображение приведено на рисунке 13.26.

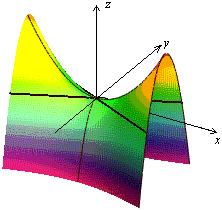
Рис.13.26.Гиперболический параболоид