60. Уравнение прямой в е3 , проходящей через две данные точки.
Извините ничего не нашла.
61. Общее уравнение прямой в Е3 . Угол между двумя прямыми в Е3 . Условие перпендикулярности прямой и плоскости.
Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.
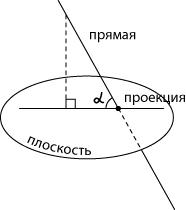
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.
Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.
Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много.
На практике применяется признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
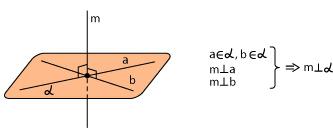
62. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямых. Точка пересечения прямой и плоскости.
Рассмотрим прямую l с направляющим вектором а и плоскость р с нормальным вектором п. Обозначим через φ угол между прямой l и плоскостью р, а через ψ — угол между векторами а и n. Легко видеть, что φ = 90° — ψ , если ψ < 90° (рис. 209, а) и φ = ψ — 90°, если ψ > 90° (рис. 209,6).
В обоих случаях справедливо равенство sin φ = | cos ψ) |.
По формуле (1) § 20 находим
и, следовательно,
Если известны прямоугольные декартовы координаты направляющего вектора прямой и нормального вектора плоскости a = (a1; a2; a3) и n = (А; В; С), то угол φ может быть вычислен с помощью формулы
(1)
63. Поверхности второго порядка в е3 . Цилиндрические поверхности.
Поверхности второго порядка – это поверхности, которые в прямоугольной
системе координат определяются алгебраическими уравнениями второй степени.
1. Эллипсоид.
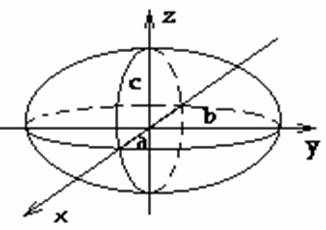
Эллипсоидом
называется поверхность, которая в
некоторой прямоугольной системе
координат определяется уравнением:
(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного
эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких
плоскостей определяется уравнением вида z=h, где h – любое
число, а линия, которая получается в сечении, определяется двумя уравнениями
(2)
Исследуем уравнения (2) при различных значениях h.
1)
Если
>
c
(c>0), то
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости
z=h с данным эллипсоидом не существует.
2)
Если
,
то
и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c)
(плоскости
касаются эллипсоида).
3)
Если
,
то уравнения (2) можно представить в виде
откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с
полуосями
и
.
При уменьшении
значения
и
увеличиваются
и достигают своих наибольших значений
при
, т. е. в сечении эллипсоида координатной плоскостью Oxy получается
самый
большой эллипс с полуосями
и
.
Аналогичная картина получается и при пересечении данной поверхности плоскостями,
параллельными координатным плоскостям Oxz и Oyz.
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как
замкнутую овальную поверхность (рис. 156). Величины a, b, c называются
полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.