Тема 13. Аналіз розподілу однієї змінної. Перевірка статистичних гіпотез: z-тест, t-тест Ст’юдента для однієї вибірки.

Повернімося до прикладу із застосуванням ліків, що підвищують рівень інтелекту.

Ген сукупність (200 осіб). μ₁= 100 (IQ)

Випадково вибрали 16 осіб.

Застосували до них ліки, які підвищують IQ. Їхнє M_s = 107,75 (IQ)

M_s – μ₁ = 7,75;

Запитання: Чи ця різниця спричинена застосуванням ліків, чи помилкою вибірки?

μ₂ (середнє уявної генеральної сукупності після застосування ліків) – невідоме...

Гіпотеза 0. μ₂= 100, значима різниця між μ₂ та М_s спричинена помилкою вибірки, а застосування ліків не мало суттєвого ефекту. Здійснюємо припущення, що Гіпотеза 0 вірна.

Гіпотеза 1. μ₂≠ 100, різниця між μ₂ та М_s незначима, отже застосування ліків мало суттєвий ефект.

У відповідності до викладеного в попередній лекції матеріалу тут нам необхідно обчислити ймовірність події – різниця між середнім значенням вибірки (Ms) і популяції (μ2) є спричиненою помилкою вибірки. Такого змісту результат статистичного спостереження не є суперечливим зі змістом Гіпотези-0, що надало б нам можливість аргументовано інтерпретувати Гіпотезу-0 як коректну, а також що означало б, що вагомих контраргументів проти змісту Гіпотези-0 не знайдено.

Отже, якщо ймовірність зазначеної вище події є малою, то це означає, що малим є й відсоток ризику допуститися помилки, відхиляючи Гіпотезу-0 як фальшиву. Приймаємо рішення відхилити Гіпотезу-0.

Якщо ж ймовірність зазначеної вище події є великою, то це означає, що великим є й відсоток ризику допуститися помилки, відхиляючи Гіпотезу-0 як фальшиву. Приймаємо рішення зберегти Гіпотезу-0.

Для того, щоб розв’язати це завдання, для початку моделюємо велику кількість випадкових вибірок, кожна з яких є обсягом 16 осіб з популяції у 200 осіб (ІЛЮСТРАЦІЯ-1).

Ця ж модель з багатьох випадкових вибірок передбачає, що кожна з вибірок має своє середнє значення, відмінне як від генеральної сукупності, так і від інших вибірок.

Це означає, що середнє змодельованих вибірок має певну варіацію, певний розподіл. Отже моделюється теоретичний розподіл середніх значень вибірок.

Теорема центрального ліміту.

Для вибірки, об’ємом не менше 25, розподіл середніх значень багатьох однакових до неї вибірок, відібраних з однієї генеральної сукупності, наближається до нормального. Цей розподіл також має своє середнє значення і своє стандартне відхилення середнього значення (стандартну помилку середнього значення (SE)).

(ІЛЮСТРАЦІЯ-2).

Формула для обчислення стандартного відхилення середнього значення (SE):

, де σ – стандартне відхилення генеральної сукупності, N – об’єм вибірки.

Зауважте, що коли обсяг вибірки зростає, стандартне відхилення у розподілі середніх значень багатьох однакових до неї вибірок, відібраних з однієї генеральної сукупності, зменшується. Іншими словами, чим меншим є обсяг вибірки, тим більшою є варіабельність середніх значень подібних до неї вибірок.

Розрахунки для: σ=12, N=4; 16.

Використовуючи теорему центрального ліміту, повернімося до нашого прикладу.

Пригадаймо, що нам слід визначити, якою є ймовірність того, що середнє вибірки у розмірі 107,75 є випадковим, спричиненим помилкою вибірки (тобто безпідставно віддаленим від середнього генеральної сукупності у розмірі 100), а не впливом ліків, що покращують IQ.

Припускаємо, що Гіпотеза 0 вірна (передбачає, що різниця між середнім вибірки і генеральної сукупності є результатом помилки вибірки).

В цій ситуації теорема центрального ліміту нам стверджує, що розподіл середніх значень вибірок, обсягом 16, коливається довкола середнього значення генеральної сукупності розміром 100 за параметрами нормального розподілу.

Стандартне відхилення генеральної сукупності = 15.

Стандартне відхилення середнього значення вибірок (SE):

Тепер визначимо ймовірність вибірки, середнє якої є віддаленим від середнього у розподілі середніх значень вибірок на відстань 7,75, або більшу (7,75 = 107,75 – 100 (107,75 - середнє випадкової вибірки, яку ми ілюстрували на початку лекції; 100 - уявне середнє генеральної сукупності у відповідності до Гіпотези-0)) (ІЛЮСТРАЦІЯ-3).

Тут ми повинні мати на увазі, що чим сильніше середнє значення спостережуваної вибірки є віддаленим від середнього значення гіпотетичної генеральної сукупності розміром 100 (у відповідності до змісту Гіпотези-0), тим надійнішою є підстава для відхилення Гіпотези-0 як малоймовірної.

Для цього ми використаємо z-тест.

Суть z-тесту полягає у перетворенні середнього значення спостережуваної вибірки (107,75) на z-значення.

Ви знаєте формулу для перетворення будь якого чистого значення на стандартизоване:

Застосовуємо її для нашого прикладу:

Результати обчислень за цією формулою свідчать про те, на якій відстані середнє значення спостережуваної вибірки знаходиться від середнього значення генеральної сукупності у відповідності до змісту Гіпотези-0. Ця відстань промірюється у розмірності стандартного відхилення середнього значення змодельованих вибірок (стандартної помилки середнього значення (SE).

Тепер нам треба з’ясувати, який відсоток змодельованих вибірок знаходиться у секторі між середнім значенням генеральної сукупності у відповідності до Гіпотези-0 та стандартизованим значенням середнього спостережуваної вибірки (ІЛЮСТРАЦІЯ-4). Звернімося до відомої вам Таблиці. Знаходимо, що між середнім значенням спостережуваної вибірки та середнім значенням генеральної сукуності знаходить 48,08% всіх середніх вибірок, змодельованих для даної генеральної сукупності. Таким чином, у утворених “хвостах” (нижньому і верхньому) сумарно знаходиться 3,84% всіх середніх значень вибірок (1,92% + 1,92%).

Нагадаймо собі, що ми прагнемо визначити ймовірність вибірки, середнє якої є віддаленим від середнього у розподілі середніх значень вибірок на відстань 7,75, або більшу. Так от, ця ймовірність відповідає сумарному відсоткові всіх середніх значень вибірок, що потрапляють у “хвости”.

Перетворюємо 3,84% на ймовірність.

p = 3,84 / 100 = 0,0384 < p = 0,05 (меншим від стандартного альфа рівня).

Отже, ймовірність події, що у розподілі середніх значень змодельованих вибірок будуть вибірки, середнє яких є меншим за 92,25 або більшим за 107,75, є малою (p = 0,0384 < p = 0,05), то це означає, що середнє спостережуваної вибірки (M_s = 107,75) є обґрунтовано (активно) віддаленим від середнього гіпотетичної генеральної сукупності (μ₂= 100 у відповідності до змісту Гіпотези-0).

Іншими словами, оскільки ймовірність події, що середнє значення вибірки у розмірі 107,75 є випадковим (спричиненим помилкою вибірки (тобто є безпідставно й неактивно віддаленим від середнього значення генеральної сукупності у розмірі 100), а не впливом ліків, що покращують IQ), є меншою за 0,05 (критичне значення для α), то в такому випадку Гіпотезу-0 відхиляємо як необґрунтовану, а Гіпотезу-1 залишаємо як достатньою мірою обґрунтовану.

Отже, вибірка зі середнім IQ у розмірі 107,75 (суттєво віддаленим від стартового середнього генеральної сукупності розміром 100,00) була не випадковою, а продиктованою впливом ліків, які застосували для покращення IQ у представників досліджуваної генеральної сукупності.

* * *

В нашому прикладі стандартизоване значення для M_s=107,75 дорівнювало 2,07. У відповідності до ІЛЮСТРАЦІЇ-4 кількість вибірок, середнє значення яких є або більшим за 107,75, або меншим за 92,25, складає 3,84% від загальної кількості змодельованих вибірок. Це було підставою для відхиляння Гіпотези 0, оскільки ймовірність вибірок, середнє яких буде або більшим за 107,75, або меншим за 92,25, склала 0,0384, що є меншим від критичного значення цієї ймовірності, розміром 0,05.

Виникає питання: Яким має бути розмір стандартизованого значення, щоб відповідна ймовірність складала якраз 0,05, тобто дорівнювала його критичному значенню? Відповідь – 1,96 (ІЛЮСТРАЦІЯ-5).

Критичне стандартизоване значення = z* = |1,96| для α=0,05.

Таким чином, як тільки стандартизоване середнє значення вибірки є більшим від |1,96|, відповідне середнє значення потрапляє в один з регіонів відкидання Гіпотези 0, а тому Гіпотеза 0 відхиляється.

Рівень α=0,05, який ми визначили як критичний для відповідної ймовірності називається рівнем значущості. Він може бути меншим, наприклад 0,01, або більшим, наприклад 0,07. Рівень α=0,05 називається стандартним рівнем значущості.

Отже, модифікована процедура тестування гіпотез зі застосуванням z-тесту виглядає наступним чином:

1. Формулюємо відповідні Гіпотезу-0 та Гіпотезу-1. Гіпотеза-0 зазвичай стверджує, що середнє значення вибірки має випадковий (недостатньо обгрунтований) зв’язок із генеральною сукупністю, що має середнє значення, визначене у відповідності до певних критеріїв (у відповідності до впливу певного зовнішнього фактора). Припускаємо, що Гіпотеза-0 є коректною.

2. Встановлюємо рівень значущості для α (0,05 стандартний). Визначаємо критичне значення для z (z*=1,96 – стандартне), яке відокремлює від загального розподілу середніх значень змодельованих вибірок регіони відкидання Гіпотези 0.

3. Трансформуємо середнє значення вибірки до z-значення за формулою:

, де – середнє значення вибірки, – середнє значення генеральної сукупності, змодельоване у відповідності до Гіпотези-0, – стандартне відхилення генеральної сукупності, – об’єм вибірки.

Беремо до уваги абсолютне значення |z|.

4. Якщо |z| > z*, тоді відхиляємо Гіпотезу-0 і доходимо до висновку, що середнє генеральної сукупності, з якої сконструйовано вибірку, не є тим значенням, яке визначає Гіпотеза-0. Це означає, що вплив зовнішнього фактора на середнє значення генеральної сукупності є відчутним.

Якщо |z| < z*, тоді зберігаємо Гіпотезу-0 і доходимо до висновку, що у нас немає вагомих аргументів стверджувати, що генеральна сукупність, з якої ми сконструювали вибірку, є інакшою від тієї, яку обумовлює Гіпотеза-0. У зв’язку з цим приймаємо рішення про слабкий вплив зовнішнього фактора на середнє значення генеральної сукупності.

Для прикладу здійснимо тестування гіпотез у випадку із перевіркою дії ліків “Super-IQ”, встановивши альфа рівень у розмірі 0,01.

1. H₀: M_s= μ₂ = 100 (ліки є не ефективними)

H₁: M_s= μ₂ ≠ 100 (ліки є ефективними)

Припускаємо, що Гіпотеза-0 є вірною.

2. Встановлюємо альфа рівень у розмірі 0,01. Визначаємо критичне значення для z, використовуючи таблицю. z* = 2,58.

3. Обчислюємо z-значення для середнього спостережуваної вибірки:

z = 2,07.

4. Оскільки |2,07| < 2,58, зберігаємо Гіпотезу-0 і доходимо висновку, що ліки є не ефективними.

Приклади різних параметрів для обчислень:

				z	z* для відпо-відного α	Дія стосовно Гіпотези 0
107,75	100	15	16	2,07	1,96 для 0,05	відкидаємо
107,75	100	15	16	2,07	2,58 для 0,01	приймаємо
107,75	100	25	16	1,24	1,96 для 0,05	приймаємо
107,75	100	15	10	1,63	1,96 для 0,05	приймаємо
110,25	100	15	16	2,73	1,96 для 0,05	відкидаємо
107,75	105	15	16	0,73	1,96 для 0,05	приймаємо

Односторонній z-тест versus двохсторонній z-тест

В попередньому прикладі при відхилянні Гіпотези-0 ми однаковою мірою враховували як дуже малі значення середнього вибірки, так і дуже великі. Отже, ми відхиляли Гіпотезу-0 як у випадку розташування середнього значення вибірки у нижньому регіоні відкидання Гіпотези-0, так і у випадку розташування середнього значення вибірки у верхньому регіоні відкидання Гіпотези-0. Такий тип тесту називається двохстороннім тестом.

Бувають ситуації, коли ви прагнете визначити, чи дія зовнішнього фактора має ефект, враховуючи певний напрям, тобто чи він ймовірно змінить середнє значення вибірки тільки у одному напрямі. Наприклад, Ви досліджуєте ймовірний вплив ліків, які підвищують IQ, і при цьому вас не цікавить ситуація, коли зазначені ліки понижують IQ. В такому випадку вам слід застосовувати односторонній тест.

Якщо Гіпотеза-1 стверджує, що ліки підвищують IQ, тоді Гіпотеза-0 повинна стверджувати, що ліки не підвищують IQ. Тут слід звернути увагу на наступну обставину: якщо Гіпотеза-0 стверджує, що ліки не підвищують IQ, це є те саме, що стверджувати, що ліки або залишають IQ на старому рівні, або понижують його. Тобто:

H₀: M_s= μ₂ < 100. (ІЛЮСТРАЦІЯ-6)

Після обчислень відповідного стандартизованого значення виникає запитання: “Як інтерпретувати отриманий результат, враховуючи обидва змісти Гіпотези-0 (обидва графіки на ІЛЮСТРАЦІЇ-6)?”

Для ситуації, коли M_s= μ₂ = 100, ми вже знаємо як діяти, адже ми знаємо розрахункове середнє значення генеральної сукупності, а також відповідний регіон відкидання Гіпотези 0 для нас визначено. Однак в ситуації, коли M_s= μ₂ < 100, ми не маємо визначених ані розрахункового середнього значення генеральної сукупності, ані меж для регіону відкидання Гіпотези 0. Як в такому випадку діяти?

Тут діє наступний принцип: якщо у вас є підстави відхилити Гіпотезу-0, яка стверджує, що M_s= μ₂ = 100, то це є достатнім аргументом також для відкидання Гіпотези-0, яка стверджує, що M_s= μ₂ < 100.

Отже, для нашого прикладу, зміст гіпотез має виглядати наступним чином:

H₀: M_s= μ₂ < 100;

H₁: M_s= μ₂ > 100.

Зауважте, що помилковим було би наступне формулювання гіпотез:

H₀: M_s= μ₂ = 100; (ліки не мали жодного впливу на IQ)

H₁: M_s= μ₂ > 100,

оскільки тут порушено принцип симетрії/ взаємодоповнюваності змісту гіпотез.

Зміст гіпотез може виглядати також наступним чином:

H₀: M_s= μ₂ > 100;

H₁: M_s= μ₂ < 100.

Для одностороннього тесту також інакшим є критичне стандартизоване значення (z*).

Візьмемо до уваги ситуацію, коли ми враховуватимемо дуже високе середнє значення вибірки для відкидання Гіпотези-0 (так, як на ІЛЮСТРАЦІЇ-6). Отже:

1. H₀: M_s=μ₂ < 100;

H₁: M_s=μ₂ > 100.

2. Студенти самі обчислюють z* для даного одностороннього тесту, у випадку, якщо α = 0,05 (ІЛЮСТРАЦІЯ-7). z*=1,65.

3. Обчислюємо стандартизоване значення для = 107,75.

4. Оскільки |2,07| > 1,65, то в такому випадкові приймаємо рішення про відхиляння Гіпотези 0 та про збереження Гіпотези-1.

5. Робимо висновок про те, що ліки мали відчутний вплив на підвищення IQ.

Зверніть увагу, що якщо у прикладі із ліками, що мають підвищувати рівень інтелекту, середнє вибірки є меншим за середнє генеральної сукупності, визначене у відповідності до змісту Гіпотези-0, а тому, наприклад, знаходиться на протилежному боці у розподілі середніх подібних до неї вибірок стосовно регіону відкидання Гіпотези-0, то тоді односторонній z-тест не проводиться, а Гіпотеза-0 інтерпретується як коректна.

Таким чином, односторонній z-тест проводиться тільки тоді, коли середнє вибірки є у тій самій частині розподілу середніх вибірок, де знаходиться регіон відкидання Гіпотези-0 (ІЛЮСТРАЦІЯ-8).

Отже:

Якщо ви прагнете встановити, чи зовнішній фактор мав хоча б якийсь вплив на досліджувану вами характеристику генеральної сукупності, то тоді використовуйте двохсторонній тест при співставленні середніх значень вибірки та генеральної сукупності.

Якщо ви прагнете встановити, чи зовнішній фактор мав у певному напрямі скерований вплив на досліджувану вами характеристику генеральної сукупності, то тоді використовуйте відповідний односторонній тест при співставленні середніх значень вибірки та генеральної сукупності.

Таблиця критичних значень для z (z*):

	односторонній тест	двохсторонній тест
для α = 0,05	1,65	1,96
для α = 0,01	2,33	2,58

t-тест Ст’юдента для однієї вибірки

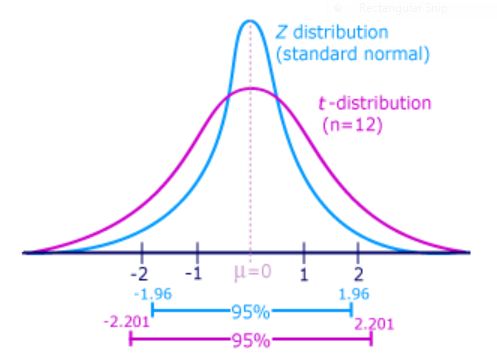
При проведенні z-тесту ми припускали, що нам відоме стандартне відхилення генеральної сукупності, однак, у більшості випадків воно є невідомим. За таких обставин проводиться t-тест Ст’юдента для однієї вибірки. Тут невідоме стандартне відхилення генеральної сукупності також обчислюється /оцінюється з використанням параметрів вибіркової сукупності. При цьому, із врахуванням того, що зазначене оцінювання впроваджує додаткову варіабельність у розподілі середніх значень змодельованих вибірок, це компенсується за рахунок встановлення ширших/ більших меж для критичних значень при проведенні t-тесту Ст’юдента, ніж при проведенні z-тесту. Це означає, що при проведенні t-тесту Ст’юдента встановлюються суворіші стандарти для відхилення Гіпотези-0, ніж при проведенні z-тесту (ІЛЮСТРАЦІЯ ЦЬОГО).

, де s – розрахункове / оціночне стандартне відхилення генеральної сукупності.

Таким чином, t-тест Ст’юдента обчислює оціночну кількість одиниць стандартного відхилення, що означає відстань середнього значення певної вибірки від середнього значення у розподілі подібних вибірок, сконструйованих у відповідності до середнього значення генеральної сукупності, що відповідає змістові Гіпотези-0.

Приклад:

Фірма запроваджує нову харчову добавку, що сприяє швидкому схудненню.

При цьому вона рекламує, що ви втрачатимете в середньому по 7 кг ваги щомісяця, якщо щодня вживатимете її. Щоб перевірити правдивість цієї реклами, ви відібрали 10 добровольців, які протягом місяця слідували інструкціям фірми з метою схуднення. Заміри після місяця вживання добавки показали наступну втрату ваги добровольцями (в кг):

4,3; 4,4; 3,5; 6,7; 6,9; 5,2; 9,3; 5,8; 4,1; 1,5

Середнє = 5,17. Оскільки воно є меншим за рекламованих 7, вам слід встановити, чи це є реальні показники, і реклама є неправдивою, чи ці показники є результатом помилки вибірки.

Отже, для початку ми маємо визначити, яким є s – розрахункове / оціночне стандартне відхилення генеральної сукупності, оскільки цей параметр нам невідомий.

, де N – об’єм вибірки, а – корекційний фактор, оскільки стандартне відхилення вибірки є завжди меншим за стандартне відхилення відповідної генеральної сукупності.

Чим меншим є об’єм вибірки, тим більшою є різниця між відповідними стандартними відхиленнями, а тому тим більшим має бути корекційний фактор.

Наприклад, для вибірки 2 корекційний фактор = 1,4, а для вибірки 100 = 1,005.

Формула для обчислення стандартного відхилення вибірки:

Отже,

Формула для обчислення реального стандартного відхилення генеральної сукупності:

Формула для обчислення розрахункового / оціночного стандартного відхилення генеральної сукупності:

ЗНАЙДІТЬ 2 ВІДМІННОСТІ.

Отже:

Після здійснення певних математичних перетворень для обчислення s, отримуємо остаточну (зручнішу) формулу для його розрахунку:

В такому випадку остаточна формула для обчислення t виглядає наступним чином:

Як зазначено вище, при проведенні t-тесту Ст’юдента встановлюються ширші/ більші межі для критичних значень, ніж при проведенні z-тесту. Це означає, що при проведенні t-тесту Ст’юдента встановлюються суворіші стандарти для відхилення Гіпотези-0, ніж при проведенні z-тесту.

Крім цього слід враховувати також те, що для менших вибірок слід встановлювати ширші/ більші межі для критичних значень, ніж для більших вибірок. Це пов’язане з тим, що стандартні відхилення менших вибірок сильніше відрізняються від стандартних відхилень відповідних генеральних сукупностей, а більших вибірок – слабше, а тому для менших вибірок слід застосовувати потужніші корекційні фактори.

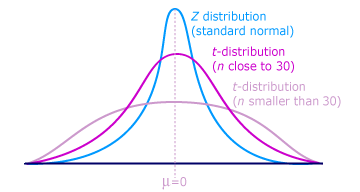
Отже, критичні значення для t (t*) варіюють в залежності від взаємодії наступних трьох факторів:

а) об’єму вибірки;

б) рівня значущості для α;

в) чи проводиться одно- або двохсторонній тест.

У зв’язку з цим для визначення t* використовують наступну таблицю (TABLE t*).

У цій таблиці df – ступінь свободи, який для t-тесту однієї вибірки обчислюється як N-1, де N – об’єм вибірки. Якщо обчислене вами df ви не знайшли в таблиці, тоді використовуйте найближче до нього менше значення. Наприклад, якщо обчислене вами df=50, тоді обираємо 40. Це визначить дещо більше значення t* для відхилення Гіпотези-0, ніж потрібно, тобто – з певним запасом.