Градуировка шкалы электронного измерителя деформации

Чтобы узнать цену деления прибора, проводим тарировку или градуировку датчика.

Для этой цели создаем известную деформацию и снимаем показания прибора. Поделив одно на другое, узнаем, скольким единицам деформации соответствует одно деление прибора.

Для градуировки используем тарировочную балку (рис. 4.5 в журнале). Это балка равного сопротивлении, т.е. в такой балке напряжение постоянно по всей длине балки. Докажем сначала, что в рассматриваемой балке имеет место условие σ = const. Изгибающий момент при изгибе консольной балки изменяется по закону М_x = Fz, где F – нагрузка, приложенная к концу балки (в нашем эксперименте это вес гирь), z – расстояние от конца балки до рассматриваемого сечения (рис.4.5). Напряжение при изгибе равно , М_x это изгибающий момент, а - момент сопротивления изгибу сечения балки на расстоянии z от конца, ширина балки в этом сечении равна b(z) = . Подставим выражения для М_x и W_x в формулу для напряжения: Доказали, что напряжение постоянно по длине балки. Докажем теперь, что балка равного сопротивления изгибается по дуге окружности. Это означает, что кривизна такой балки постоянна, т.е. При изгибе балки продольная деформация равна . Датчик приклеен на поверхности балки, значит, он измеряет деформацию слоя, у которого

( y это расстояние от точки, в которой определяется деформация, до нейтрального слоя, т. е. до оси балки). Из закона Гука ( ) следует, что деформация равна . Значит, кривизна тарировочной балки при изгибе равна , т. е. балка изгибается по кривой с постоянной кривизной, а это дуга окружности.

Во время эксперимента на каждом этапе нагружения записываются показания реохорда

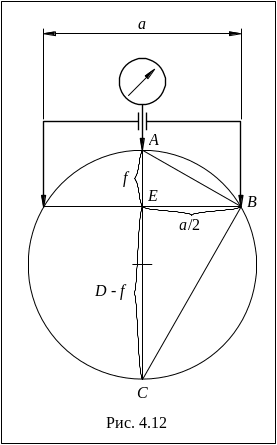
(т. е. фиксируется деформация) и снимаются показания индикатора. Индикатор измеряет величину f, это высота сегмента окружности, по которой выгибается балка, рис. 4.12 (и рис. 4.6 в журнале). Осталось выяснить, как, зная f, определить деформацию ε.

На рис. 4.12 в треугольнике АВС сторона АС это диаметр, ВЕ – перпендикуляр, опущенный из вершины прямого угла на диаметр. Из геометрии известно, что в таком случае величина ВЕ в квадрате равна произведению АЕ на ЕС, или

, но f  D, тогда можно принять (D - f) D и

и кривизна балки равна .

Деформация при будет .

Получили выражение для деформации, исходя только из геометрических соображений, не используя закон Гука, так как модуль Юнга нам еще предстоит определить.

Лабораторная работа № 5

ПРЯМОЙ ИЗГИБ

Б рус, работающий на изгиб, называется балкой. Изображенная на рисунке балка, прямолинейная до изгиба, после изгиба приобретает криволинейную форму. На этом рисунке v - прогиб балки по оси y, - угол поворота оси балки (+ против часовой стрелки), - радиус кривизны изогнутой оси балки.

Поскольку мы рассматриваем только такие балки, у которых прогиб v очень мал, то и угол поворота тоже очень мал. Тогда . Но тангенс угла наклона кривой это первая производная от функции, описывающей эту кривую, в нашем случае от функции прогиба v. Значит, = . Таким образом, угол поворота оси балки это первая производная от функции прогиба v.

Из математики известно, что кривизна кривой . В нашем случае при очень малых перемещениях и углах поворота <<1, поэтому можно считать , откуда получается , т.е. кривизна изогнутой оси балки это вторая производная от функции прогиба.

На лекциях в разделе «Изгиб» была получена зависимость между изгибающим моментом и кривизной оси балки . Из двух выражений для кривизны получается .

Для определения перемещения с помощью дифференциального уравнения упругой линии (т.е. изогнутой оси балки) надо изобразить балку без опор, заменив их найденными реакциями.

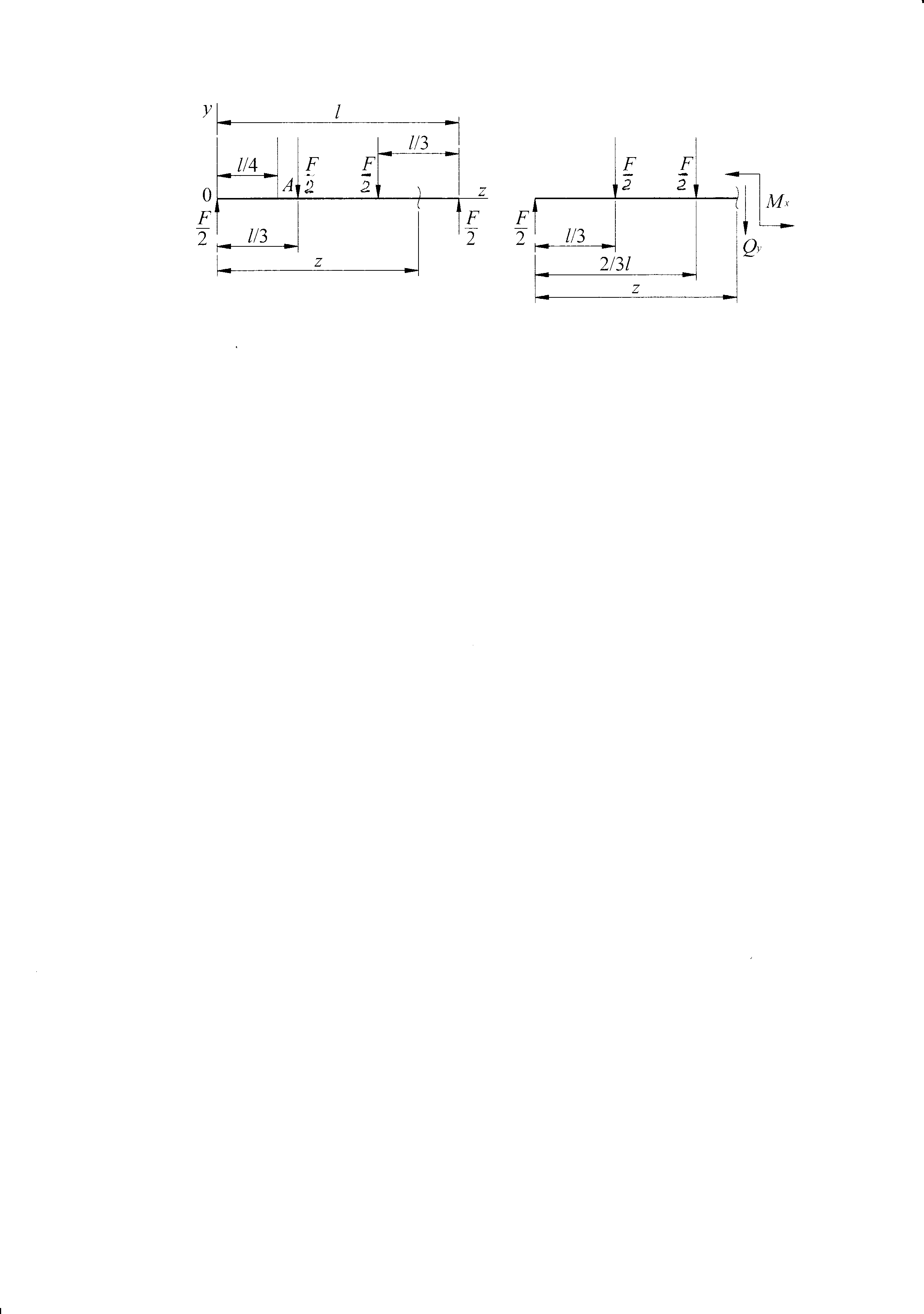
Проводим оси z, y, поместив начало координат слева там, где была опора, z – от начала координат. Разрезаем балку в пределах последнего участка. В сечении прикладываем положительные силовые факторы: изгибающий момент дает сжатые слои сверху, поперечная сила направлена вниз.

Запишем выражение изгибающего момента для этого сечения, используя полученное выше выражение момента через его кривизну

.

Это уравнение кривизны оси балки, интегрируем его, не раскрывая скобок .

Получили уравнение углов поворота оси балки. Константа первого интегрирования С это угол поворота оси балки в начале координат, умноженный на жесткость.

Интегрируем выражение еще раз

.

Получили выражение для прогибов балки v. Это уравнение является универсальным. Будучи функцией прогибов для последнего участка балки, это выражение включает в себя функции прогибов всех предыдущих участков. Чтобы найти прогиб на любом из предыдущих участков, надо из универсального уравнения взять только члены, относящиеся к этому участку – это силовые факторы, лежащие левее сечения, в котором определяем перемещение (смотри на сайте http://steandr.clan.su раздел «Определение перемещений с помощью дифференциального уравнения»).

Константа D это прогиб в начале координат, умноженный на жесткость. В нашем случае в начале координат была опора, прогиб на которой равен нулю. Отсюда константа D=0.

Для определения константы С используем граничное условие на правой опоре: Подставив это условие в функцию прогибов, получим (при D=0)

.

Знак минус у константы С означает, что угол поворота оси балки в начале координат отрицательный, т.е. по часовой стрелке. Это соответствует форме изогнутой оси балки.

Сечение «А», в котором нам предстоит определить прогиб, находится на расстоянии от начала координат. Это первый участок, значит, из универсального уравнения возьмем только члены, лежащие левее этой точки, подставив найденное значение константы С и

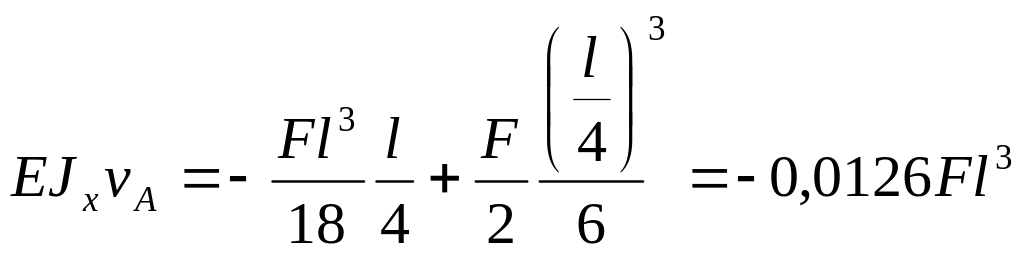, откуда прогиб в сечении «А» равен

Дальнейший расчет проводим в ньютонах и метрах. Подсчитаем осевой момент инерции сечения. Тонкостенный профиль следует разбить на полоски – вертикальную и две горизонтальных. Используя теорему Штейнера об изменении моментов инерции при параллельном переносе осей, получим

, в метрах это будет .

Нагрузка F=1000н, длина балки l=0,9м, модуль Юнга материала балки Е=0,7∙10 ⁵ МПа, отсюда

Знак минус означает, что перемещение будет в сторону отрицательной оси y, т.е. вниз.