7

ЛАБОРАТОРНЫЕ РАБОТЫ ПО СОПРОМАТУ, ЧАСТЬ 1

Работы №1,2,3,4,5,6

Механические характеристики материалов, используемые при расчетах на прочность, определяются экспериментально на стандартных образцах. Основными являются испытания на растяжение, сжатие, кручение. В результате испытаний получается кривая в координатах нагрузка – перемещение, называемая характеристикой образца. С помощью определенных формул эта характеристика образца преобразуется в кривую, построенную в координатах напряжение – деформация. Такая кривая называется диаграммой или характеристикой материала.

Материалы можно разделить на пластичные материалы, типичные примеры которых это малоуглеродистая сталь, медь, алюминий, и хрупкие материалы, такие, например, как серый литейный чугун, высокопрочные стали.

Лабораторная работа №1

ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ ОБРАЗЦОВ МАТЕРИАЛА

Для испытаний на растяжение используется десятикратный образец (рис.1.1 в журнале), у которого l₀ = 10 d₀. Здесь l₀ – база испытаний. Это отмеченный на образце отрезок его длины, изменения которого фиксируются при эксперименте как Δl – удлинение образца, d₀ – первоначальный диаметр образца. Образец растягивают до тех пор, пока он не разрушится. После испытаний получается характеристика образца в координатах F, Δl. С помощью формул и из характеристики образца получается диаграмма (характеристика) материала в координатах - напряжение, - деформация.

Испытание малоуглеродистой стали - типичного пластичного материала

Участки характеристики образца

ОА - линейный участок, материал подчиняется закону Гука, удлинение образца, пропорциональное растягивающей силе F, определяется по формуле . До точки В деформации полностью упруги. Если в точке В начать разгружать образец, то самописец но линии разгрузки ВАО вернется в начало координат и образец приобретет свои первоначальные размеры.

CD - горизонтальный участок диаграммы - площадка текучести, деформации интенсивно нарастают при постоянной нагрузке.

DE - зона упрочнения: к точке D в кристаллах металла закончилась перестройка, и материал может снова сопротивляться нагружению.

EG - зона разрушения.

В точке Е при максимальной нагрузке в образце возникает местное утонение - шейка. Дальнейшие деформации сосредотачиваются в районе шейки, которая при этом интенсивно утоняется. Деформировать образец становится легче, поэтому нагрузка уменьшается и кривая идет вниз. После разрыва образца материал в районе шейки теплый. Это зона больших пластических деформаций, при образовании которых материал нагревается.

На характеристике образца с помощью геометрических построений находят характерные точки, соответствующие силам F_пц, F_y, F_т, F_max, F_раз. Затем, подсчитав по приведенным выше формулам напряжения σ и деформации έ, строят диаграмму (характеристику) материала, с помощью которой определяют механические характеристики материала:

- предел пропорциональности - наибольшее напряжение, до которого справедлив закон Гука (s = E e), т. е. напряжения пропорциональны деформациям;

- предел упругости - наибольшее напряжение, до которого деформации полностью упруги, т. е. целиком исчезают при разгрузке;

- предел текучести - напряжение, при котором деформации интенсивно нарастают при постоянной нагрузке;

- предел прочности - напряжение, численно равное максимальной нагрузке, деленной на первоначальную площадь сечения образца.

Характеристика стали называется условной, так как она получена на основании формул и , где A₀ и l₀ - первоначальная площадь сечения и первоначальная длина образца, в то время как при растяжении изменяются как длина образца, так и размеры его сечения. Если учитывать эти изменения, то получим истинную диаграмму, изображенную тонкой линией на рис. 1.12. Только на истинной диаграмме есть напряжение при разрыве , это самое большое значение напряжения во время испытаний. A_min - площадь сечения шейки в месте разрыва, , d_min - диаметр шейки в месте разрыва. При растяжении стальной образец интенсивно деформируется. Остаточное удлинение после разрыва достигает 30%.

Образец после разрыва

На условной характеристике напряжения при разрыве нет!

В конструкциях, как правило, материал работает при напряжениях, меньших предела текучести. Как видно из рис. 1.12, условная и истинная диаграммы практически совпадают и до значения напряжения, равного пределу текучести s_т. Поэтому на практике используют для расчетов условную диаграмму.

Закон разгрузки и повторного нагружения

Если материал нагрузить за пределы упругости и разгрузить, то при разгрузке исчезнут только упругие деформации, а пластические деформации останутся (рис. 1.14). Согласно рис.1.14, образец нагружен за пределы упругой зоны (точка К находится выше точки В, соответствующей пределу упругости). Затем образец разгружают. Линия разгрузки KL параллельна первоначальному участку диаграммы ОА (точка А соответствует пределу пропорциональности). При вторичном нагружении (линия LK) материал сохраняет пропорциональную зависимость между нагрузкой F и удлинением Dl (то есть между s и e) вплоть до максимального напряжения первичного нагружения (точка K), а затем следует по первоначальной кривой КЕ.

Таким образом, за счет нагружения материала за пределы упругой зоны и дальнейшей разгрузки, увеличивается предел пропорциональности материала до значения максимального напряжения первичного нагружения (т. К на диаграмме). Это свойство материалов используется на практике, например, при заневоливании пружин. После изготовления пружины нагружают за пределы упругости, увеличивая тем самым величину осадки пружины, пропорциональную силе.

На рис. 1.14:

OАВK - линия первичного нагружения;

KL - линия разгрузки;

OL - пластическое или остаточное удлинение образца;

LM - упругое удлинение, исчезающее при разгрузке;

LKE - линия вторичного нагружения.

Условный или технический предел текучести

Н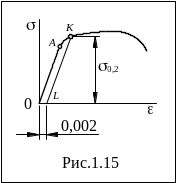 екоторые пластичные материалы, например, алюминий, не имеют площадки текучести на диаграмме. Для таких материалов используется условный или технический предел текучести

s_0,2 - это напряжение, при котором остаточная деформация равна 0,2%, то есть это величина 0,002 в масштабе диаграммы, рис. 1.15.

Имея диаграмму материала, можно определить условный передел текучести графически (рис. 1.15). Для определения s_0,2 сначала отложим по оси e величину остаточной деформации, равную 0,002 в масштабе диаграммы. Затем проведем линию разгрузки LK÷÷ ОА. Получим пересечение этой линии с кривой (точка K). Соответствующее точке K напряжение и есть условный или технический предел текучести s_0,2.

Испытание серого литейного чугуна - типичного хрупкого материала

При растяжении хрупкий материал разрушается при малых деформациях ( доли процента), без образования шейки, максимальное напряжение и напряжение при разрыве совпадают (рис.1.16) Для таких материалов определяется предел прочности при растяжении

На рис. 1.17 приведены характеристики стали и

чугуна при растяжении. Уклон графика в начале координат пропорционален модулю упругости материала Е. Поскольку модуль упругости стали в два раза больше модуля упругости чугуна, то уклон начального участка диаграммы у этих материалов отличается. Предел прочности чугуна при растяжении меньше предела текучести стали при растяжении

Перестройка машинной диаграммы при испытании образца на растяжение

( Кривая в первой четверти)

Испытательная машина записывает кривую в координатах сила – перемещение. Это машинная диаграмма. По вертикальной оси сил записывается истинное значение нагрузки. По горизонтальной оси перемещений, кроме удлинения образца, записываются еще удлинения и перемещения всех частей машины, находящихся на одной линии с образцом. Эти лишние перемещения надо исключить и оставить по оси только удлинение образца.

Перестройка машинной диаграммы

1-й способ (ось сил вертикальная)

Для произвольного значения силы F по формуле вычисляем удлинение образца Δl. На взаимно перпендикулярных осях (F– вертикальная ось, Δl – горизонтальная) откладываем эти значения F и Δl, получаем точку. Обозначим эту точку буквой К. Из начала координат (точки О) проводим прямую через эту точку К. Полученная прямая ОК есть начальный участок характеристики образца. Затем продлим прямолинейный участок машинной диаграммы (отрезок ОL). Теперь все точки машинной диаграммы надо сместить влево на величину горизонтальных отрезков, заключенных между этими лучами ОК и ОL. Например, берем точку на машинной диаграмме, проводим горизонтальную линию, замеряем отрезок между лучами ОК и ОL и откладываем этот отрезок от данной точки влево. Получаем положение этой точки на характеристике образца. Обведя сдвинутые точки, получим характеристику образца. Чтобы получить значение силы для любой точки этой кривой, опускаем из точки перпендикуляр на ось Δl, измеряем вертикальный отрезок, учитываем масштаб. Это будет сила F.

Удлинение образца в этом способе это отрезок от начала координат до точки пересечения с осью Δl перпендикуляра, опущенного из данной точки на ось Δl.

2-й способ (ось сил наклонная)

В этом способе не кривая «подтягивается» к оси сил, а ось сил наклоняется к кривой. Продлив прямолинейный участок машинной диаграммы, на этой наклонной прямой отложим отрезок - произвольное значение силы F. От полученной точки влево по горизонтали отложим значение удлинения Δl, соответствующее этой силе (расчет, как в предыдущем способе). Через полученную точку и начало координат проводим луч (например, ОК). Эта наклоненная линия есть ось сил для характеристики образца. Кривую не надо перестраивать. Чтобы получить значение силы для любой точки этой кривой, как и в предыдущем методе, опускаем из данной точки перпендикуляр на ось Δl, измеряем вертикальный отрезок, учитываем масштаб. Это будет сила F (по оси сил ошибки нет).

Удлинение образца в этом способе это расстояние по горизонтали от данной точки кривой до наклонной оси сил.

Лабораторная работа №2

ИСПЫТАНИЕ НА СЖАТИЕ ОБРАЗЦОВ МАТЕРИАЛА

Для испытаний на сжатие используется цилиндрический образец, , рис. 2.11.

Испытание малоуглеродистой стали

- предел текучести стали при сжатии.

С таль при сжатии не разрушается, но интенсивно деформируется. Возникающие на торцах образца силы трения мешают материалу перемещаться в радиальном направлении. Вследствие этого образец пластичного материала при сжатии приобретает бочкообразную форму, рис. 2.12. Для устранения этого нежелательного явления, искажающего характеристику материала, следует уменьшать силы трения на торцах. С этой целью либо помещают пропитанные парафином прокладки на торцах образца (парафин не выдавливается при больших давлениях), либо используют специальные трубчатые образцы с конусными концами, где тангенс угла a этого конуса равен коэффициенту трения пары материалов образец - нажимная плита, рис. 2.13. Малоуглеродистая сталь работает одинаково на растяжение и сжатие, т. е. предел текучести при растяжении s_тр равен пределу текучести при сжатии s_тс и обозначается просто s_т.