Б. Дисконтирование

Дисконтированием называется исчисление первоначальной суммы денег на основании ее конечной величины. Таким образом, дисконтирование – обратная операция по отношению к нахождению будущей стоимости.

Например, если кто-то хочет иметь на своем счете 150 руб. через год при процентной ставке 50% годовых, то сегодня ему надо вложить в банк 100 руб. Расчет прост:

В общем случае вопрос звучит так: какую сумму денег (K₀) надо положить сегодня на счет, чтобы через год там было K₁ руб., если процентная ставка составляет i% годовых? Ответ:

Поставим вопрос в самом общем виде: какую сумму денег надо положить сегодня в банк, чтобы через n лет на счете было K_n руб.? Теперь ответ будет зависеть от того, какой процент начисляет банк: простой или сложный.

Если процент простой, то:

Если процент сложный, то:

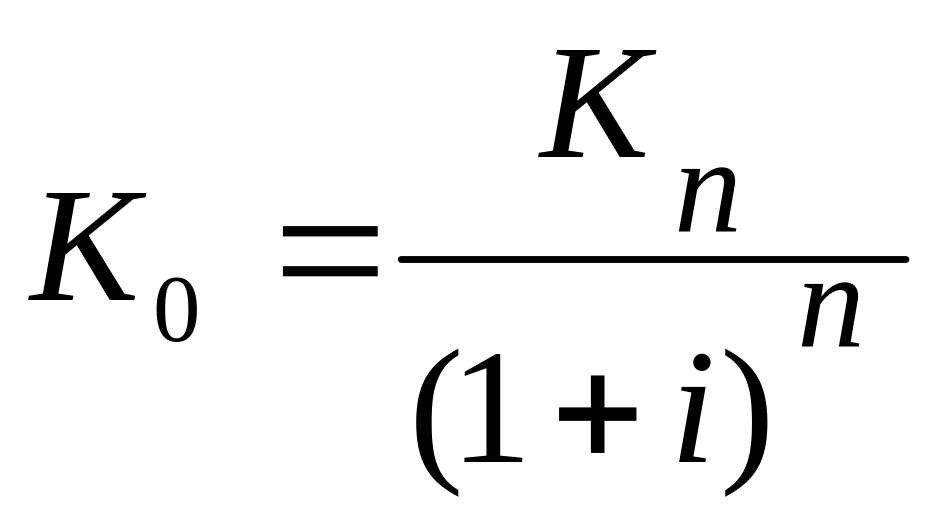
Путем дисконтирования можно определить, какой сумме денег сегодня эквивалентна некоторая сумма, которая будет получена в будущем (FV). Тем самым мы можем рассчитать приведенную (сегодняшнюю) стоимость будущих денежных поступлений (PV).

Важнейший постулат финансового анализа состоит в том, что деньги имеют различную временную ценность: некоторая сумма денег сегодня предпочтительнее той же суммы, которая будет получена позднее. Это объясняется тем, что сегодняшние деньги индивид уже может как-то использовать, повышая свое благосостояние. Финансовые аналитики при этом рассматривают только одну возможность – положить деньги в банк, и тогда их сумма возрастет.

Допустим, перед Вами альтернатива: получить 100 руб. сейчас или только через год. Для простоты предположим, что риск неполучения денег в будущем равен нулю, а инфляция отсутствует – цены через год не изменятся. Пусть банки при этом платят по вкладам 20% годовых.

Очевидно, что при таких условиях Вы предпочтете получить деньги немедленно, поскольку, вложив их банк сегодня, Вы получите через год уже 120 руб. Иными словами, 100 руб. сегодня имеют для Вас большую ценность, чем 100 руб. через год.

А если альтернатива звучит так: 80 руб. сегодня или 100 руб. через год? Ответ базируется на той же логике: вложив 80 руб. в банк Вы получите через год 96 руб., что меньше 100 руб. Это означает, что с позиций финансового аналитика 100 руб. через год предпочтительнее 80 руб. сегодня.

Какой же сумме денег сегодня равны 100 руб., получаемые через год? Ответ получается дисконтированием 100 руб. по банковской процентной ставке: . В самом деле, вложив 83,33 руб. сегодня в банк можно получить через год 100 руб. Вам поэтому безразлично, получить 83,33 руб. сегодня или 100 руб. через год – эти суммы имеют для Вас одинаковую ценность при заданной процентной ставке.

В общем виде, обозначив сумму, получаемую через год – FV₁, получаем ее приведенную стоимость: .

Таким образом, при начислении сложных процентов приведенная стоимость денег, которые будут получены один раз через n лет (FV_n), рассчитывается по формуле: .

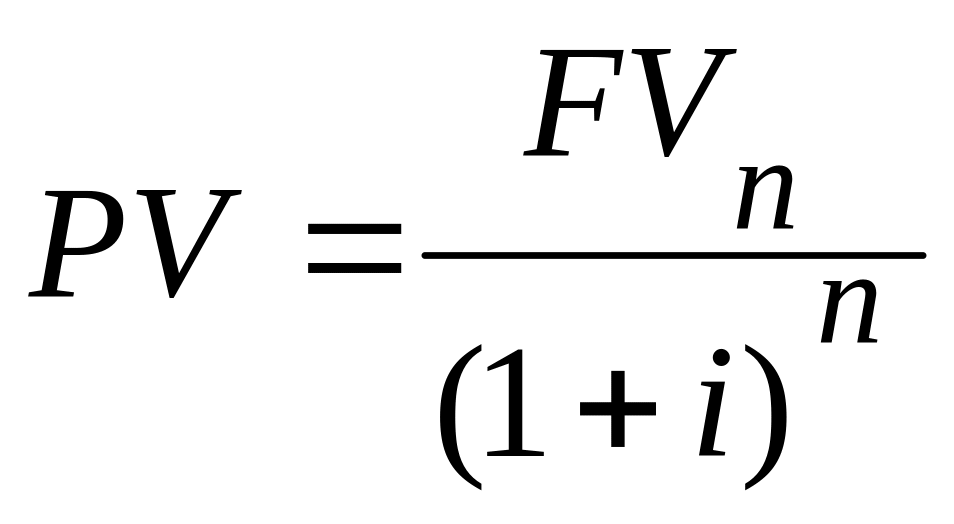Усложним модель. Предположим, Вы решили сдать квартиру на 5 лет. По договору в конце каждого года арендатор будет платить Вам 3000 долл. Сколько денег Вы получите за все время аренды? Формально: 15000 долл., но нельзя забывать, что деньги, получение которых растянуто во времени, имеют не одинаковую ценность. В частности, 3000 долл., причитающиеся Вам через год, совсем не равны той же сумме, получаемой через 5 лет. Поэтому просто суммировать или вычитать можно только те деньги, которые пришли или ушли примерно в одно и то же время.

В Вашем случае все будущие доходы надо сначала привести к сегодняшнему дню путем дисконтирования по банковской процентной ставке и только потом их суммировать. В результате будет получена приведенная стоимость всей величины будущих доходов:

Таким образом, если некто будет ежегодно получать некоторые суммы денег (FV_j) руб. в течение n лет, приведенная стоимость всей суммы будущих поступлений составит:

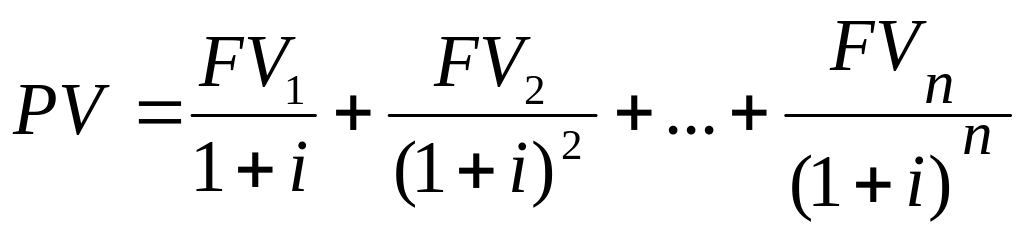
Если доход, получаемый каждый год постоянен (FV), имеем геометрическую прогрессию со знаменателем 1/(1+i):

Отсюда:

Если число лет бесконечно велико (n), формула упрощается:

На основе дисконтирования можно решать задачи на погашение займов. Пусть некто взял заем под сложные i% годовых. Выплата в j-ый год составляет FV_j. Продисконтировав эту выплату по процентной ставке, находим ее приведенную стоимость:

В момент, когда сумма всех дисконтированных выплат становится равна первоначальному долгу, последний считается погашенным.

В качестве примера предположим, что взаймы взяты 100 руб. на 2 года под 100% (i=1) годовых. В первый год заемщик выплатил кредитору 100 руб. В результате погашены только 50 руб. займа, поскольку:

Во второй год выплачено еще 200 руб. Продисконтировав эту сумму, находим:

Таким образом, сумма дисконтированных выплат за два года составила величину займа – 100 руб. (50+50=100). Долг погашен.