5. Линии влияния усилий составных конструкций

типа многопролетных балок

Рассмотрим многопролетную балку (рис. 137а). Построим для нее «этажную схему». Построим вначале линии влияния для опорных реакций.

Л.В.

Построим Л.В. для балки 1 - 2 – 3 (рис. 137в). Силу Р = 1 будем далее передвигать по балке 3 – 4, которая находится выше балки 1 – 3 и передает

нагрузку и на балки 1 – 3 и на балку 4 – 5 – 6. Когда груз Р = 1 находится над опорой 3 балки 3 – 4, он полностью воспринимается балкой 1 – 3, т. е. величиной в/а (рис. 137в). Двигаясь по балке к опоре 4, груз Р = 1 будет меньше передавать усилие на балку 1 – 3 и больше - на балку 4 – 6. Когда груз Р = 1 будет находиться над опорой 4, реакция опоры 3 будет равна нулю, следовательно, на балку 1 – 3 он не передает свое влияние и будет равна также нулю. И когда Р = 1 будет передвигаться по балке 4 – 6 и далее, он не передает влияния на балку 1 – 3, т. к. груз с нижних этажей не передается на верхние.

Аналогично строятся Л.В. реакций других опор (рис. 137г, д, е).

Рассуждая таким же образом, мы можем построить Л.В. и для внутренних усилий в различных сечениях балки.

6. Вычисление усилий по Л.В. от неподвижной нагрузки

Обратимся к Л.В. усилия R_A простой балки (рис. 138). Отметим, что при нахождении силы Р = 1 на опоре А величина реакции равна 1, а при нахождении силы Р = 1 на расстоянии х от опоры А величина R_A будет равна величине R_A(х), взятой из графика (рис.138). Если силу Р = 1 увеличить в «n» раз, то и график (его значения) увеличится в «n» раз.

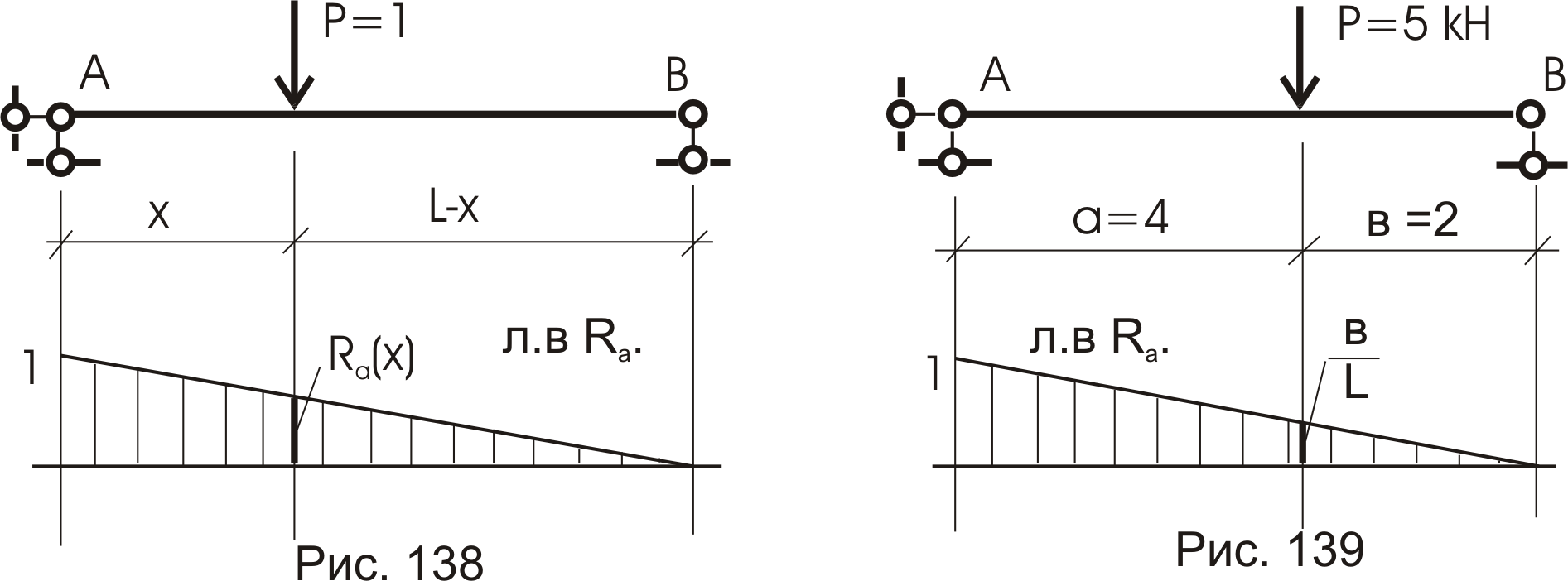
Тогда при загружении одной сосредоточенной силой, скажем, Р = 5 кн (рис.139), величина R_A будет равна произведению силы 5 (кн) на ординату Л.В. R_A, взятую под силой, т. е.

или, вычисляя аналитически, получим то же значение R_A.

Если же балка или другая конструкция нагружена сосредоточенными силами и, пользуясь принципом независимости действия сил, вычислим значения усилия от каждой силы и результаты сложим, т. е.

,

где: Р_i – значение сосредоточенной i-ой силы;

y_i – ордината Л.В. усилия S, взятая под силой Р_i (на рис.140 –л.в. R_A), т. е.:

.

Если конструкция нагружена равномерно распределенной нагрузкой (рис. 141), то усилие S будет подсчитываться как произведение интенсивности

нагрузки на площадь (-Ω) Л.В. усилия (на рис. 141 л.в. усилия М_к), т. е. или для М_к:

.

Пример.

Конструкция (рис.142в) нагружена системой сил (вариант а и вариант б).

Вычислим значения усилий по линиям влияния Н₃ (рис. 142г), М_к (рис. 142д), М_F (рис. 142е).

Загружение по варианту «а».

Загружение по варианту «б»

8 Определение перемещений в упругих системах

1. Общие понятия.

Определение перемещений в упругих системах от статической нагрузки необходимо:

а) при расчете конструкций (системы) по деформациям (проверка конструкций по допускаемому прогибу-перемещению);

б) при расчете статически неопределимых систем, когда наряду с уравнениями статики рассматриваются уравнения совместности деформаций.

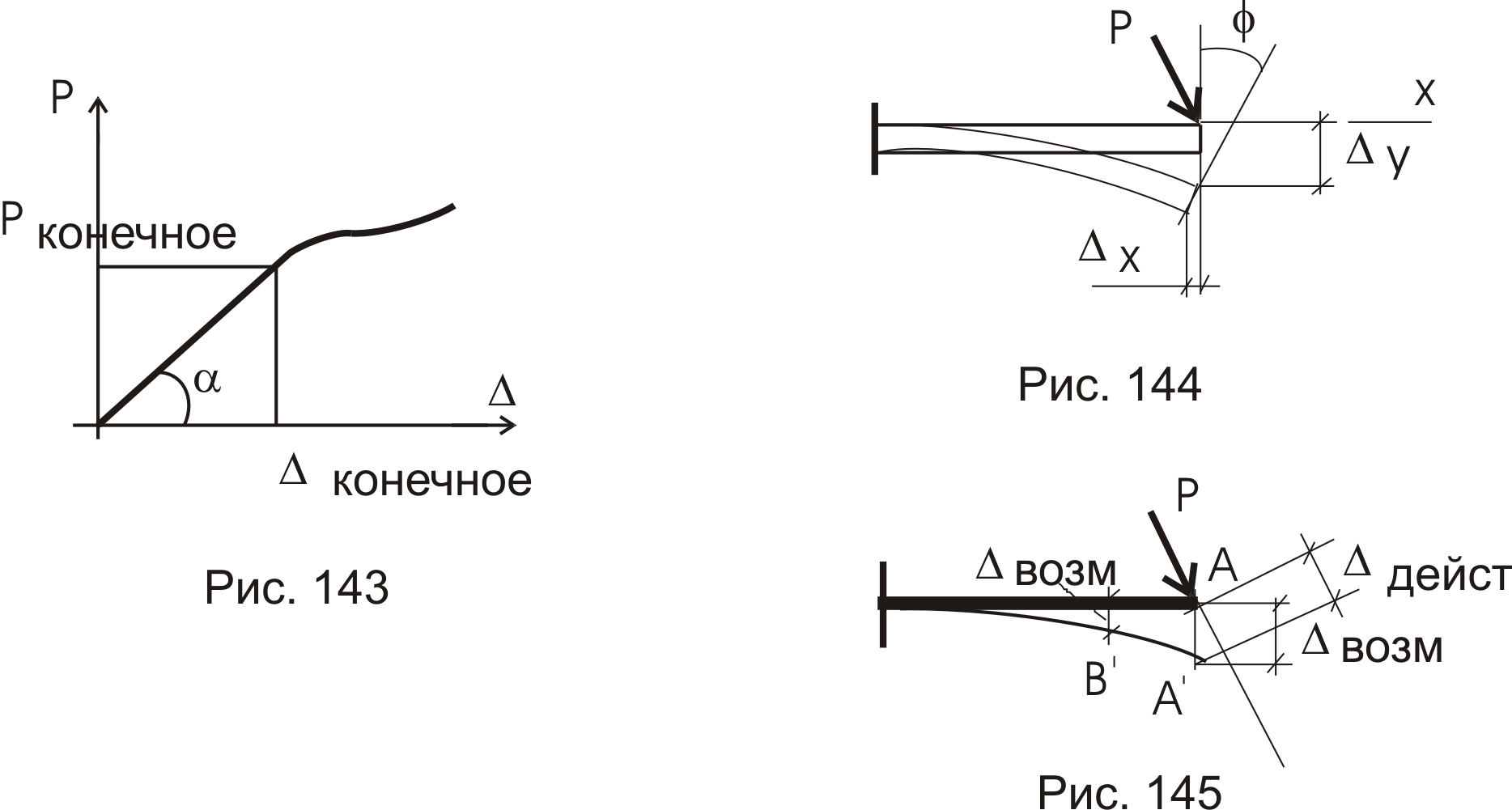
• Статическая нагрузка – нагрузка, прикладываемая к системе, возрастает от нуля плавно, не вызывая сил инерции в материале конструкций, до конечного значения.

• К упругим системам (конструкциям) относятся системы, материал которых работает только в зоне упругих деформаций (рис. 143). В этом случае имеем:

,

где: и Р –конечные значения перемещения и прикладываемой нагрузки, соответственно;

- коэффициент пропорциональности.

• Перемещения точек сооружения (системы) возникают: от нагрузки; вследствие упругих свойств материала; от осадки опор сооружения; от неточности сборки; от воздействия на материал сооружения температуры.

Перемещения различаются: на линейные и угловые (для сечения) (рис. 144); на действительные и возможные (рис. 145).

Линейные перемещения – поступательные перемещения (чаще по горизонтали и вертикали).

Угловые перемещения – поворот сечения.

Действительное перемещение есть перемещение точки приложения силы по ее направлению и для данной силы оно одно.

Возможное перемещение – перемещение точек сооружения от заданной силы и их множество (рис. 145).

• Понятия обобщенная сила и обобщенное перемещение.

Рассмотрим систему сил, приложенную на простую балку (рис. 146). Эти силы вызовут деформацию балки. Для каждой силы имеем деформации точек их приложения.

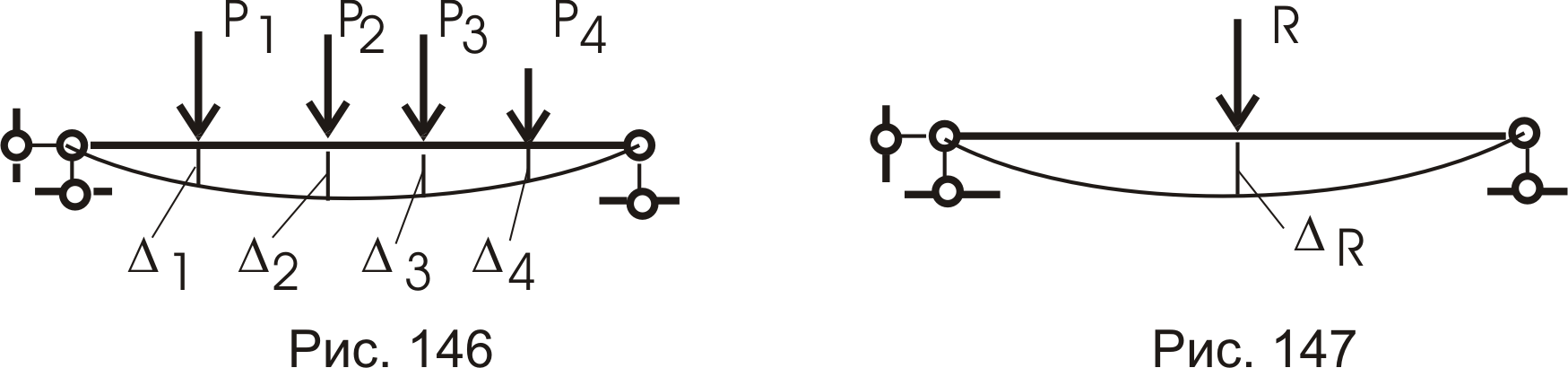
Каждую систему сил мы можем привести к их равнодействующей:

и приложим ее к балке (рис. 147). Она вызовет деформацию балки.

В данном случае:

- обобщенная сила;

- обобщенное перемещение.

Данное понятие позволяет нам последующие рассуждения и доказательства проводить на примере одной силы (обобщенной).

2. Действительная работа внешних сил.

Работа статически приложенной силы на действительном ее перемещении называется действительной работой.

Построим график изменения силы и перемещения (рис. 148а). Сила Р возрастает от нуля до конечного ее значения, перемещение при этом возрастает прямо пропорционально, т. е.

.

Работа силы численно будет равна площади заштрихованного треугольника, а именно:

.

Действительная работа внешних сил равна половине произведения окончательного значения силы на окончательное значение перемещения.

3. Возможная работа внешних сил

Работа силы на возможных перемещениях называется возможной работой.

Отметим, что сила имеет уже окончательное значение (рис. 148б) и на возможном перемещении, вызванном какими-либо факторами, она совершает работу на конечном перемещении в виде прямоугольника, т. е.

.

`

4. Действительная работа внутренних сил

При воздействии на сооружение внешних сил, внутренние силы упругого тела совершают действительную работу на действительных перемещениях - .

Рассмотрим элементарный элемент длиной dx .

К нему будут приложены силы: N, Q, M.

Рассмотрим их действие по принципу независимости действия сил.

а) Продольное усилие – N (рис. 149).

Элементарная работа запишется :

^,

где - действительное перемещение от силы N. В свою очередь, , тогда

^.

б) Перерезывающая сила Q.

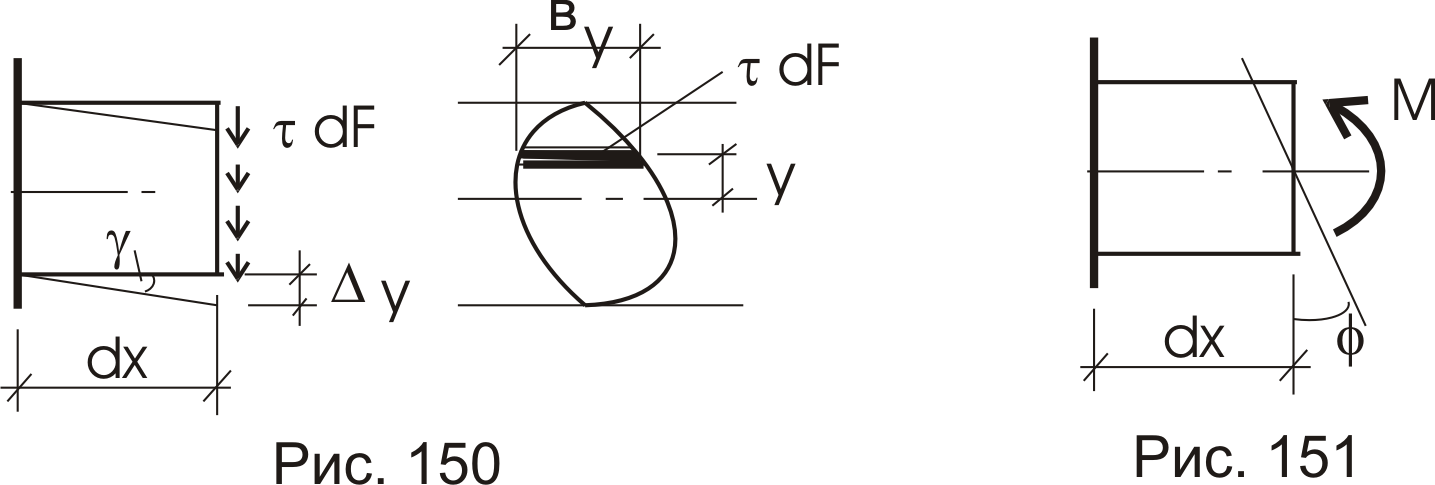
Касательное усилие совершит работу на перемещении , где ; в свою очередь ; подставим значения (рис. 150):

Касательное напряжение и перерезывающая сила связаны соотношением:

где: - статический момент верхней или нижней части сечения относительно ординаты y;

J – момент инерции сечения;

b_y – ширина сечения на высоте y;

G – модуль упругости при сдвиге.

Подставим выражение в , получим после интегрирования по dF

.

Величины, не зависящие от F, вынесем за знак интеграла

.

Умножим и разделим на F, получим:

.

Окончательно имеем:

.

в) Изгибающий момент – М (рис. 151).

, здесь ,

тогда

Полная работа внутренних сил запишется:

или

.

Теперь интегрируем по длине элемента и суммируем все элементы, входящие в конструкцию (систему), и получим:

.

5. Возможная работа внутренних сил

Рассмотрим два состояния системы (рис. 152а,б).

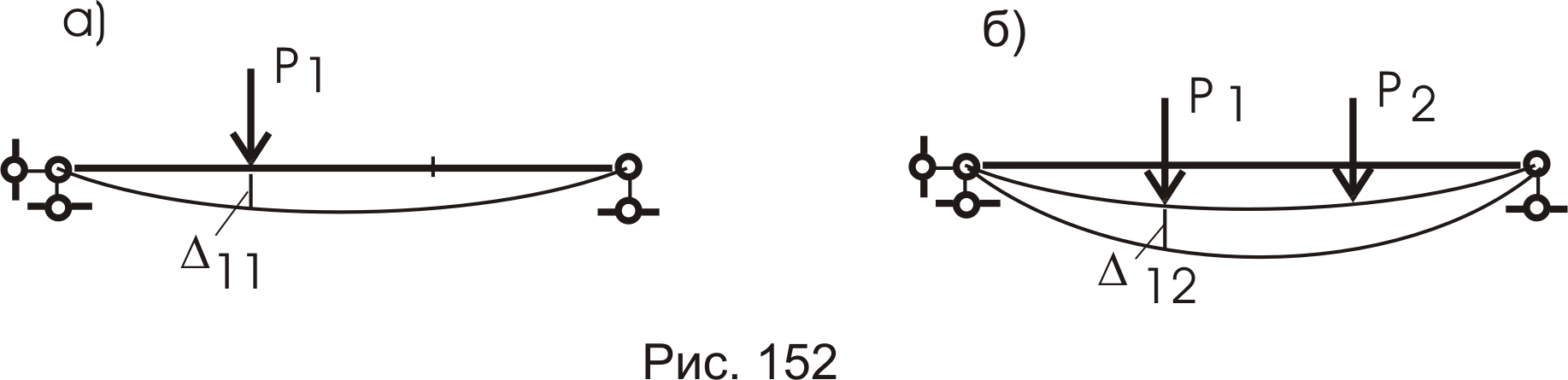
В первом состоянии сила P_b вызывает внутренние усилия M₁, Q₁, N₁.

Во втором состоянии, при приложении силы P₂ к деформированной конструкции, в конструкции возникнут деформации: , которые, в свою очередь, могут быть выражены через усилия:

.

При деформации системы усилия, вызванные силами первого состояния, совершают возможную работу на перемещениях, вызванных силами второго состояния

.

6. Теорема о взаимности работ

Конструкцию (балку) загрузим двумя силами, но загрузим балку двумя путями:

1. Загружение произведем поочередно: сначала силой Р₁, а затем на деформированную балку приложим силу Р₂ (рис. 153а).

Подсчитаем работу этих сил

.

2. Загружение произведем в обратном порядке (рис. 153б):

.

,

остается

или - Теорема Бетти.

Работа сил первого состояния на перемещениях, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях, вызванных силами первого состояния.