6. Построение окончательной эпюры изгибающих моментов
Воспользуемся принципом независимости действия сил:
Эпюры
представлены на рисунке
222.
Эпюра
представлена на рисунке 223.
Правильность построения подтверждается проверками: статической и кинематической.
Статическая проверка заключается в равновесии узла 2 (рис. 224).
;
,
.
Такое расхождение допустимо.
Кинематическая проверка.
Проверим перемещение узла 5 по вертикали – оно должно быть равно нулю, т. к. по этому направлению в этой точке имеется опорный стержень.
Выберем
основную систему метода сил и приложим
к точке 5 по вертикали единичную силу
(рис. 225 а). От этой силы построим эпюру
(рис. 225 б).
что составляет 0,03%.
Результаты удовлетворяют.
Эпюра Qок строится по эпюре Мок уже рассмотренными нами выше приемами (рис.226 а). Эпюра Nок строится по эпюре Qок (рис. 226 б).
3.Метод конечных элементов
1. Основные понятия.
Заданную конструкцию (раму, ферму и т. д.) разобьем на отдельные элементы (желательно простые – прямой стержень; участок стержня и т. д.). Элементы определяются самим расчетчиком. Попробуем проделать это на отдельных конструкциях.
Пример 1 (рис.227)
Можно:
1) Выделить три элемента: 1 – 2; 2 – 3; 3 – 4 (рис. 228).
2) 6 элементов: 1 – А; А – 2; 2 – В; В – 3; 3 – С; С – 4 и т. д.
Если мы учтем одно из правил изменения внутренних усилий, а именно: на незагруженном участке внутренние усилия меняются по линейному закону, то это позволит нам при распределении внешней нагрузки в узлы конструкции использовать конечные элементы в виде стержней, соединяющихся в узлах.
Распределение внешней нагрузки разберем ниже.
Пример 2 (рис.229).
Пронумеруем узлы. Пронумеруем элементы (они обозначены цифрой в кружочках). Выделим их отдельно (рис. 230).
При узловой нагрузке в этих элементах будут возникать внутренние усилия:
- в первом элементе возникает только продольное усилие (рис. 231 а).
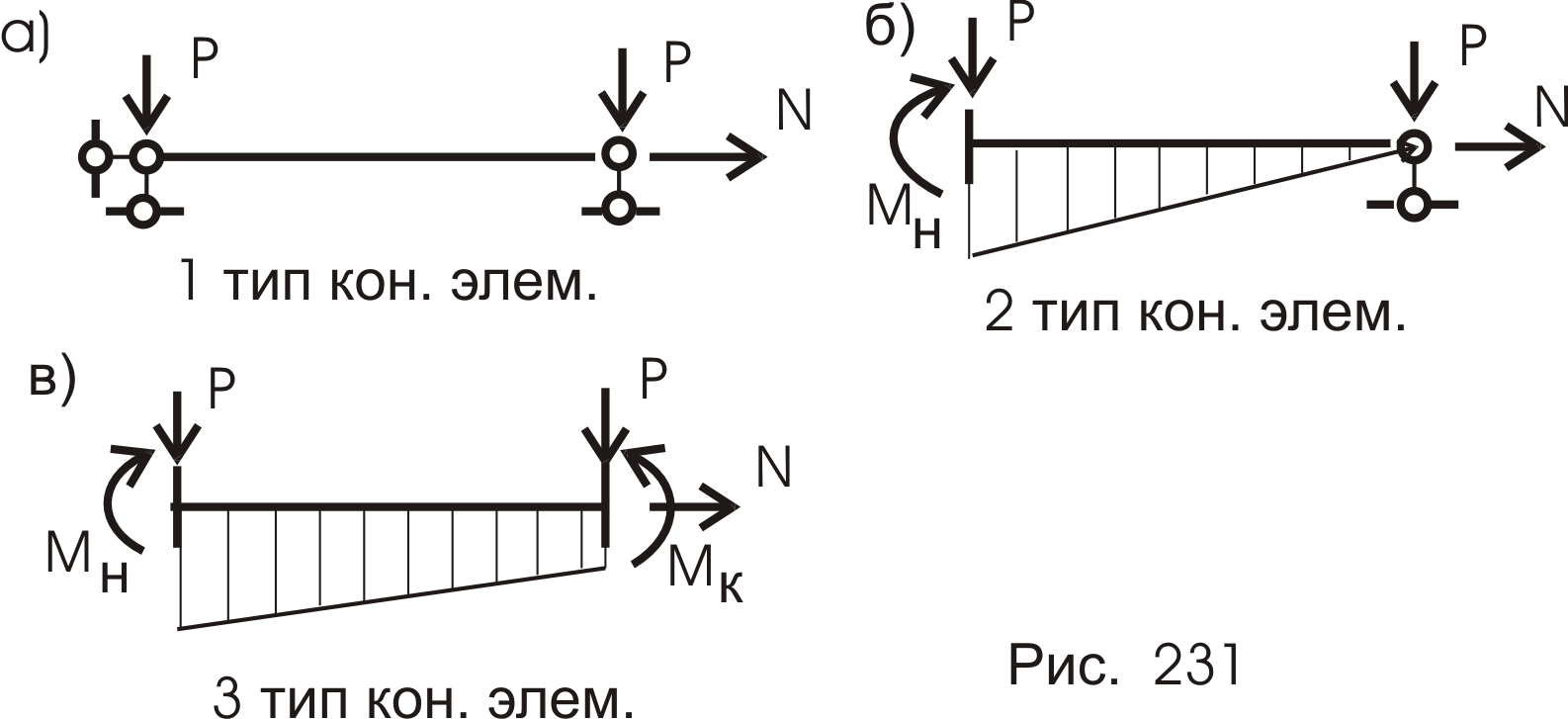
- во втором (рис. 231 б) и третьем (рис. 231 в) элементах, помимо продольного усилия, в заделках возникает изгибающий момент и он вызывает перерезывающую силу – Q.
Примем правило:
- меньший номер при нумерации узлов будем считать началом – «н», а больший номер – концом – «к» стержня;
- изгибающий момент будем направлять так, чтобы он растягивал нижние волокна.
Из рассуждений видим, что в каждом элементе возникают неизвестные силы:
- продольное усилие;
- изгибающий момент.
Перерезывающую силу можем представить (выразить) через изгибающий момент. Такой подход снижает количество неизвестных.
Определив характер неизвестных, сформируем порядок их определения.
Обратимся к примеру (рис. 232).
1. Пронумеруем узлы в произвольном порядке.
2. Жесткое соединение стержней обозначим заделкой (можно и другим способом), подобно методу перемещений (делается это для наглядности).
3. Нумеруем элементы (в произвольном порядке). Номер элемента обведем в кружочек.
4. Нагрузку, действующую на элемент, распределяем на его узлы.
Элемент 1 (рис. 233). Строим эпюру изгибающих моментов и определяем опорные реакции. Можем воспользоваться схемами метода перемещений. Исходя из решения, получаем узловую нагрузку на элемент.
Элемент 2. Нагрузка на элемент показана на рисунке 234.
Элемент 3 (рис. 235).
Если табличных решений нет, данную балку можем решить одним из рассмотренных выше способов.
Воспользуемся уравнением 3-х моментов неразрезной балки:
или
Опорные реакции обозначены на рисунке 235.
Отсутствие нагрузки на элементе 4 дает нулевую нагрузку на его узлы. Полученная узловая нагрузка для каждого элемента дает общую схему нагружения конструкции в целом (рис. 236).
Для наглядности дальнейших расчетов вычертим эпюры неизвестных изгибающих моментов и продольных усилий согласно принятым нами правилам (рис. 237 а,б).
По этим эпюрам мы легко просчитаем количество неизвестных и составим матрицу-столбец неизвестных усилий (представим матрицу усилий в виде матрицы-строки):
,
где Ni – продольное усилие в i – ом элементе;
и
- изгибающие моменты в начале (н) и конце
(к) i-го
элемента.
Связь между усилиями и внешней нагрузкой осуществляется посредством уравнений равновесия. Для этого воспользуемся вырезанием узлов (в любой последовательности). При составлении уравнений равновесия примем правила:
- ось х направим вправо;
- ось y направим вверх;
- изгибающий момент положительный, если он направлен относительно узла против часовой стрелки (рис. 238).
Вырезаем узел 2 (рис. 239). Моменты и линейные усилия (N и Q) представим для наглядности на отдельных рисунках.
1.
;
2.
;
3.
.
Перерезывающие силы выразим через изгибающие моменты
; 
; 
.
Перепишем уравнения равновесия, перенеся грузовые слагаемые в правую часть
1.
.
2.
.
3.
.
Узел 4 (рис. 239 справа).
4.
,
5.
,
где
;
Тогда после подстановки Q4 и Q3 уравнения 4, 5 примут вид:
4.
.
5.
.
Полученные уравнения равновесия позволяют сформировать матрицу равновесия А из коэффициентов при неизвестных и матрицу Р – вектора нагрузки, а именно:
Количество строк матрицы соответствует количеству уравнений равновесия, а количество столбцов – количеству неизвестных. И если количество столбцов больше количества строк (прямоугольная матрица), то это говорит о статически неопределимой задаче. Вектор нагрузки (в виде матрицы-строки) запишется:
.
Тогда уравнения равновесия запишутся в матричной форме:
.
Для решения статически неопределимой задачи, как мы знаем, потребуются уравнения совместности деформации.
Раскроем их физическую суть.
Нужно помнить, что каждому виду воздействия (усилию) соответствует свой вид деформации, и для упругих систем запишем:
,
,
где В – коэффициент пропорциональности, назовем его коэффициентом податливости. Поскольку перерезывающая сила отсутствует в списке неизвестных, мы о ней говорить больше не будем.
Выявим физическую суть коэффициента податливости для продольного усилия.
Рассмотрим 1 тип конечного элемента (рис. 240):
.
Загрузим
данный элемент силой
и вычислим перемещение точки приложения
по ее направлению по формуле Мора
,
.
Тогда общее уравнение (перемещение) от силы N запишется:
или коэффициент податливости
.
Для
элемента второго типа, кроме загружения
силой
(результат нам уже известен) нужно
загрузить жесткий узел моментом
и определить от этой нагрузки угол
поворота заделки по данному направлению
(рис. 241).
.
Тогда
или
.
Учитывая, что данный элемент подвергается воздействию двух усилий, общий коэффициент податливости (он уже будет представлять диагональную матрицу второго порядка) примет вид:
В матрице податливости элемента ноль в первой строке указывает на то, что продольное усилие (N) не вызывает поворота в заделке, а ноль во второй строке указывает, что изгибающий момент не вызывает продольного удлинения стержня.
Третий тип элемента (рис. 242). Элемент подвергается трем воздействиям: N – продольной силой, Мн и Мк – изгибающими моментами в начале (н) и конце
(к) элемента. Матрица податливости В для данного элемента будет третьего порядка, а именно:
,
где
- продольное перемещение от
и равно
;
нули в первой строке указывают на то,
что продольная сила не вызывает поворота
ни в начале, ни в конце элемента;
- угол поворота начала (н) элемента от
,
и он будет равен, как и у элемента 2-го
типа
;
- угол поворота конца (к) элемента от
воздействия
,
и
- угол поворота начала (н) элемента от
воздействия
.
Нужно отметить,
;
- угол поворота конца (к) элемента от
.
,
.
Тогда матрица податливости для 3-го типа элемента запишется:
.
Матрица податливости конструкции в целом будет представлять собой совокупность матриц податливости отдельных элементов, расположенных по диагонали:
,
где n – количество конечных элементов; i – порядковый номер элемента.