7.1.2Особенности расчета оперения.

Зная нагрузки и геометрию можно получить эпюры распределения перерезывающих сил, изгибающих и крутящих моментов. Далее методикой аналогичной расчету крыла можно произвести расчте оперения. Для руля расчет еще более упрощается, вследствии того, что изгиб и сдвиг в нем работает только лонжерон с присоединенной обшивкой, а на кручение – замкнутый контур обшивки.

Однако, имеется ряд нюансов, усложняющих такой расчет. Для построения расчетных эпюр необходимо знать реакции в узлах навески руля, а это является достаточно сложной задачей и представляет собой наиболее трудоемкий этап расчета оперения. Исключением является случай двухшарнирной навески руля.

Рассмотрим расчет оперения на примере расчета оперения с рулем подвешенном на трех шарнирах.

Предполагается, что нам известно распределение аэродинамической нагрузки по оперению (по стаблизирующей поверхности и по рулю). Следовательно, нам известны погонные нагрузки и линии центров давления для стабилизирующей поверхности и для руля (рис. 5.2).

Рис. 5.2.

Предположим, что стабилизирующая поверхность и руль абсолютно жесткие на кручение. В этом случае расчетныю схему можно представить следующим образом – руль, как балка загружен погонной нагрузкой q_р и имеет три точки опоры, которые перемещаются в вертикальной плоскости вследствии изгиба стабилизирующей поверхности. Перемещения эти будут зависеть от величины реакций в опорах, от нагружения стабилизирующей поверхности и от жесткости на изгиб обеих балок. Также, на перемещения опор влияет и упругая заделка оперения на фюзеляже.

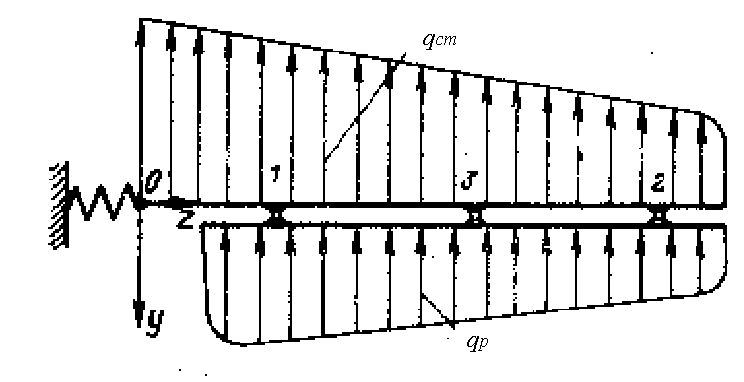
Рис. 5.3.

Данная расчетная схема отражена на рис. 5.3. Таким образом процедура определения реакций опор в данной расчетной схеме представляетсявесьма сложной. Увеличивает сложность и тот факт, что обе балки имеют, как правило, переменную по длине жесткость.

В первом приближении можно упростить расчет приняв опоры жесткими, жесткостьбалок постоянной (хотя бы в пределах одного пролета). Тогда при помощи уравнения трех моментов можно определить реакциий опор. Однако такой расчет будет очень неточным даже для первого приближения. Более точным способом расчет будет метод сравнения деформаций.

Уберем из расчетной схемы на рис. 5.3. шарнир 3 (средний). В этом случае руль будет представлять собой двухопорную балку и поскольку такая балка статически определима, то расчет ее не представляет сложностей и может быть произведен вплоть до определения прогибов.

Далее, зная реакции в шарнирах 1 и 2 легко расчитываем и консольную балку стабилизирующей поверхности, получая прогибы.

В результате точка 3, являющаяся общей для обеих балок получит разные прогибы, что является следстввием исключением шарнира 3 из системы. Реакцию в шарнире 3 найдем из условия равности перемещений точки 3 в расчетных схемах руля и стабилизирующей поверхности.

Для удобства, перемещения точки 3 будем определять относительно подвижной прямой проходящей через точки 1 и 2. До нагружения, точка 3 находится на прямой 1 – 2, под нагрузкой она сместиться на некоторое значение. В системе руля и в системе стабилизирующей поверхности это смещение будет одинаковым.

Рассмотрим порядок расчета (рис. 5.4.).

1. Определяем реакции в точках 1 и 2 – R₁₀ и R₂₀.

2. Строим эпюру перерезывающих сил Q_р0.

3. Строим эпюру изгибающих моментов M_р0.

4. Строим эпюру 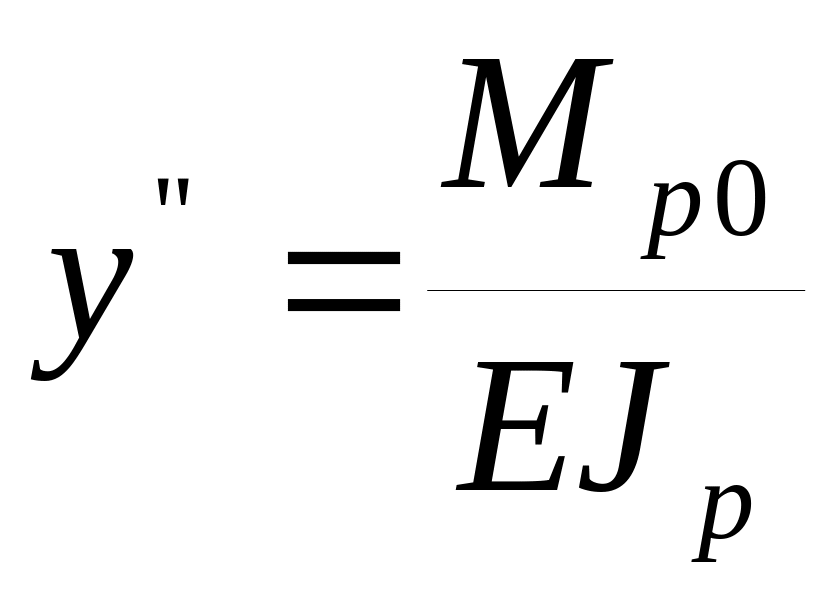. При этом не забываем, что в общем случае значение EJ_р переменное по размаху руля. Рис. 5.4.

5. Двойным интегрированием эпюры y^’’ получаем эпюру прогибов y.

6. По эпюре y получаем значение прогиба в точке 3 относительно прямой 1 – 2. Обозначим его ₃₀.

Построение эпюр в случае сложной формы распределения q_р можно производить методом трапеций при помощи таблиц, аналогично методике построения эпюр перерезывающих си и изгибающих моментов при расчете крыла в главе 3.4.1.

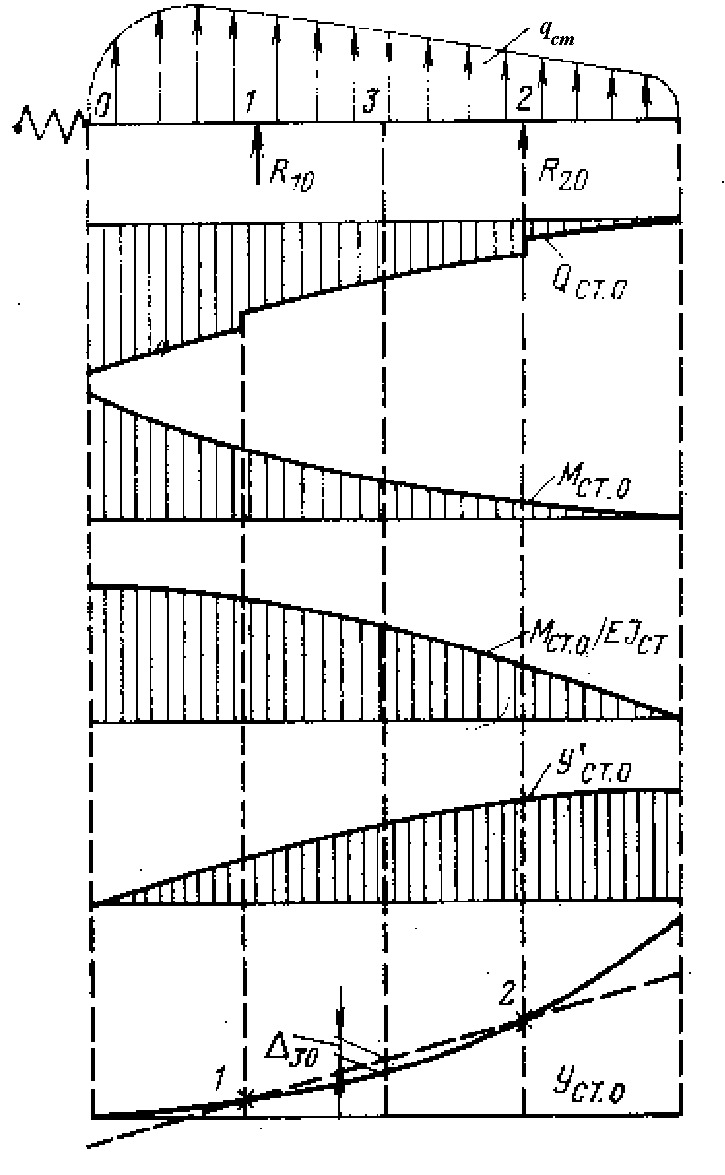
Далее производим расчет стабилизирующей поверхности, приложив значения реакций R₁₀ и R₂₀ в точках 1 и 2 с обратным знаком. Порядок расчет следующий (рис.5.5):

1. С троим эпюру перерезывающих сил Q_ст0.

2. Строим эпюру изгибающих моментов M_ст0.

3. Строим эпюру .

4. Двойным интегрированием эпюры y^’’ получаем эпюру прогибов y.

Интегрирование эпюры y^’’ в данном случае проводим от корня стабилизирующей поверхности. При этом форма кривой прогибов будет соответствовать реальной кривой прогибов (для двухопорной балки), но будет иметь смещение в вертикальной плоскости, поскольку при интегрировании от корня мы не учитываем упругость заделки. Но поскольку мы вычисляем прогиб ₃₀ относительно прямой 1 – 2, то смещение кривой прогиба не имеет значения.

Легко видеть (рис. 5.6.), что значения ₃₀ и ₃₀ не только не совпадают, но имеют разные знаки. Данное расхождение связано с тем, что при расчете мы убрали опору в точке 3. В реальной схеме данная опора присутствует и компенсирует расхождение значений ₃₀ и ₃₀. Рис. 5.5.

П риложим к точкам 3 и 3’ единичные усилия P и найдем прогибы от этих усилий. На рис. 5.7 показан процесс нахождения прогибов от единичных сил. Порядок расчета аналогичен порядку расчета прогибов для схемы с исключенной опорой 3.

Рис. 5.6.

Р ис. 5.7.

Поскольку реально в точке 3 действует сила реакции R₃, то прогибы от нее будут в R₃ раза больше. Используя принцип наложения, мы можем записать полные прогибы для руля и стабилизирующей поверхности

, (5.3)

. (5.4)

Так как точка 3 является общей и для руля, и для стабилизирующей поверхности, то

.

Следовательно

.

Из чего следует

. (5.5)

Аналогично и все остальные значения вычисляются методом наложения эпюр по формуле

, (5.6)

где A₀ – значение параметра в статически определимой системе;

A₁ – значение параметра в системе с единичным нагружением.

Таким образом, нам становятся известны значения перерезывающих сил и изгибающих моментов в сечениях руля и стабилизирующей поверхности, что позволяет перейти непосредственно к расчету. Известны также становятся и реакции во всех трех опорах. Реакцию в опоре 3 вычисляем по формуле (5.5), реакции в точках 1 и 2 по формулам (5.6):

; ; .

Дальнейший расчет сечений стабилизатора, киля и рулей на изгиб и кручение вдали от заделки производится методами, аналгичными методам расчета сечений крыла, рассмотренными в разделе 3. Стоит,однако, обратить внимание на некоторые нюансы расчета на кручение.

Р ис. 5.8.

На рис. 5.8 изображена схема нагружения стабилизирующей поверхности. Легко видеть, что в отличии от схемы нагружения крыла в выражение для крутящих моментов здесь будут входит значительные сосредоточенные силы в шарнирах руля. Соответственно, в эпюрах крутящих моментов (и в эпюрах перерезывающих сил) появятся скачки.

Расчет на кручение при этом в сечениях близким к области скачков будет ненадежным, поскольку необходимо учитывать стестненное кручение.

Особенности расчета руля на кручение. На изгиб в конструкции руля работает только лонжерон с присоединенной обшивкой, а на кручение простой замкнутый контур. Предполагая, что ось жесткости совпадает с осью лонжерона производим соответствующий расчет (данное предположение вполне допустимо для курсового или дипломногопроектов). Эпюру крутящих моментов строим обычным образом с учетом некоторых нюансов.

Рис. 5.9.

Н а рис. 5.9 показан схема нагружения руля. Подсчитывая моменты относительно оси жесткости и суммирая их получаем эпюру аналогичную эпюре на рис. 5.10. Полученный суммарный момент M_упр будет восприниматься тягой управления. Согласно рис. 5.11 очевидно, что

откуда

.

Рис. 5.10

Т ак как кронштейн управления может быть и не в конце лонжерона руля, то его момент Mупр должен быть вычтен из эпюры крутящих моментов в соответствующем сечении, как и показано на рис. 5.10.

Рис. 5.11.