5О собенности расчета крыла в зоне выреза.

Рассмотрим тонкостенное крыло с большим вырезом в межлонжеронной зоне нижней панели (рис. 5.1). В этом случае отсеки I и III имеют обычное (не нарушенное вырезом) сечение (рис. 5.2), а отсек II будет содержать два замкнутых контура (1 и 3) и один открытый контур 2 (рис. 5.3).

При нагружении такой конструкции будет наблюдаться значительное перераспределение усилий в зоне перехода от отсека I к отсеку II и в зоне перехода от отсека II к отсеку III. Например, стрингеры I-го отсека, не имея продолжения в отсеке II будут вблизи границы сдавать нагрузку сдвигом обшивки на неразрезанные продольные ребра. И, наоборот, в отсеке III эти же стрингеры будут постепенно нагружаться снимая нагрузку с неразрезанных ребер.

Рис. 5.1.

Р ассмотрим приближенный расчет зоны выреза, пользуясь принципом независимости действия сил.

Считаем, что нагрузки на крыло заданы в качестве эпюр перерезывающих сил Q_y и Q_x, изгибающих моментов M_x и M_y, а также крутящих моментов M_z.

Рис. 5.2.

Э пюры строятся обычными для крыла мтодами, описанными в разделе 3.4.

Произведем расчет на сдвиг и изгиб в двух плоскостях и кручение сечений всех трех отсеков, применяя известные методы из разделов 3.6 и 3.7.

Рис. 5.3.

Местные напряжения, вызванные перераспределением усилий на границах отсеков пока не будем принимать во внимание. Расчет для I-го и III-го отсеков сложностей не преставляет. Для расчетных сечений (включая сечения A – A и B – B, непосредственно примыкающие к границам отсека II) он будет состоять из следующих этапов (рис. 5.4):

1. Расчет на изгиб в двух плоскостях.

2. Расчет на сдвиг в двух плоскостях.

3. Определение координат центра жесткости.

4. Расчет на свободное кручение.

5. Суммирование полученных усилий.

В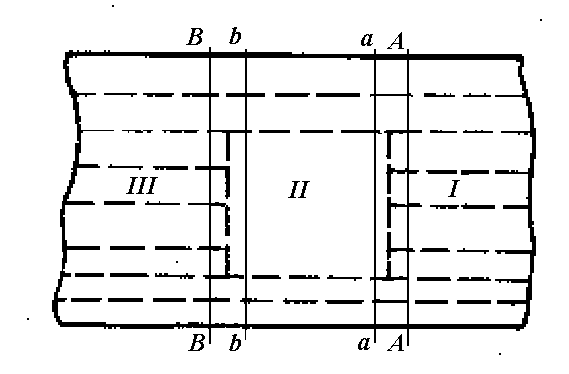 ведем обозначения:

– суммарные осевые усилия в ребрах I-го и II-го отсеков;

– соответствующие потоки касательных усилий.

Соответственно, в сечениях A – A и B – B будем иметь значения , , , .

Рис. 5.4.

Р ассмотрим более тщательно расчет II-го отсека, включая сечения a – a и b – b. Расчет на изгиб дополнительных пояснений не требует, а вот расчет на сдвиг имеет особенности в связи с тем, что средний контур сечения является открытым (рис. 5.5). Если разрезы замкнутых контуров разместить так как на рис. 5.5, то потоки касательных сил по участкам контура запишутся следующим образом:

Рис. 5.5.

Участок ABCA: ;

Участок DEFD: ;

Участок CD: .

Потоки касательных сил находятся по известной формуле

,

а и вычисляем из условий замкнутости контуров:

,

.

Коэффициенты a₂₁ = a₁₂ = 0. После нахождения находим координату центра жесткости x_ж. При необходимости проводим аналогичный расчет для Q_х и находим вторую координату центра жесткости y_ж.

Зная центр жесткости можно получить значения крутящего момента для отсека II. Однако расчет отсека II на кручение является достаточно сложным.

В замкнутых контурах 1 и 3 кручение предполагается свободным, в то время как в контуре 2 (открытом) кручение будет стесненным. Таким образом, в первую очередь необхоимо распределить крутящий момент между контурами. Для решения этой задачи заменим II-ой отсек аналогичной конструкцией с постоянным сечением, соответствующим среднему сечению II-го отсека. Приложим к этой конструкции единичный момент (рис. 5.6).

Рис. 5.6.

Доли крутящего единичного момента распределяем следущим образом

₁ + ₂ +₃ = 1. (5.1)

Для вычисления трех неизвестных ₁, ₂ и ₃ необходимо еще два уравнения. Поскольку углы закручивания контуров одинаковы, то имеем

₁ = ₂ = ₃. (5.2)

Потоки касательных сил равны

и

,

где ₁ – площадь 1-го контура;

₃ –площадь 3-го контура.

Из условия замкнутости контуров

получаем относительные углы закручивания

и

.

Угол закручивания вычисляем как интеграл

.

Следовательно

(5.3)

и

. (5.4)

Считая заделку торцевых сечений отсека абсолютно жесткой получим угол закручивания для 2-го (открытого) контура

, (5.5)

где B – расстояние между лонжеронами, ограничивающими вырез (рис. 5.6);

J₁ – момент инерции 1-го лонжерона, ограничивающего вырез;

J₂ – момент инерции 2-го лонжерона, ограничивающего вырез.

Используя формулы (5.1) – (5.5) определяем ₁, ₂ и ₃. После чего можно определить распределение моментов между контурами

,

,

.

Следовательно можно произвести расчет 1-го и 3-го контуров на свободное кручение, а 2-го на стесненное, считая заделку по торцам отсека абсолютно жесткой. В результате расчета мы получим усилия в продольных элементах и потоки касательных сил в обшивке и стенках лонжеронов. Просуммировав усилия и потоки полученные из расчетов на изгиб, сдвиг и кручения получаем суммарные продольные усилия P_i и суммарные потоки касательных сил q_i. Для сечений a – a и b – b продольные усилия и потоки касательных сил обозначим, соответственно, как , , , .

Таким образом, мы получили продольные усилия и потоки во всех трех отсеках крыла. Теперь необходимо их согласовать и скомбинировать.

По результатам предварительного расчета от внешних усилий и торцевых сил в I-ом отсеке имеем на границе с отсеком II продольные усилия и потоки касательных сил и (рис. 5.7). Данное нагружение назовем первым.

Рис. 5.7.

Очевидно, что усилия и должны удовлетворять условиям равновесия сечения

, (5.6)

, (5.7)

, (5.8)

, (5.9)

, (5.10)

. (5.11)

Рис. 5.8.

Однако, в реальности со стороны отсека II на отсек I действуют другие продольные усилия и потоки касательных сил. Второе нагружение (рис. 5.8) и , полученное из расчета отсека II, также должно удовлетворять условиям равновесия сечения.

, (5.12)

, (5.13)

, (5.14)

, (5.15)

, (5.16)

. (5.17)

Вычитая из (5.12) – (5.17) из (5.6) – (5.11) соответственно получаем

, (5.18)

, (5.19)

, (5.20)

, (5.21)

, (5.22)

. (5.23)

где

и

торцевые усилия и потоки касательных сил. Данные усилия и потоки являются взаимно уравновешенными. Допуская абсолютную жесткость нервюр можно не принимать во внимание потоки поскольку они уравновесятся на нервюре. От сил же отсек I будет загружен местными быстрозатухающими напряжениями неучтенными при расчете отсека I простыми методами.

Аналогичные рассуждения применительно к отсеку III и сечениям B – B и b – b приводят к необходимости учета торцевых сил .

Остается произвести расчет отсека I от торцевых усилий и отсека III от торцевых усилий . После чего сложить полученные напряжения с напряжениями полученными в ходе первичного расчета.