4.2Особенности расчета крыла в зоне разъема.

Рассмотрим тонкостенную конструкцию с разъемом на примере крыла. Итак, крыло имеет разрез по сечению А – А (рис. 4.2). При этом в сечении имеется n продольных ребер, из них m ребер являются «неразрезанными» (т.е. соединены узлами).

Р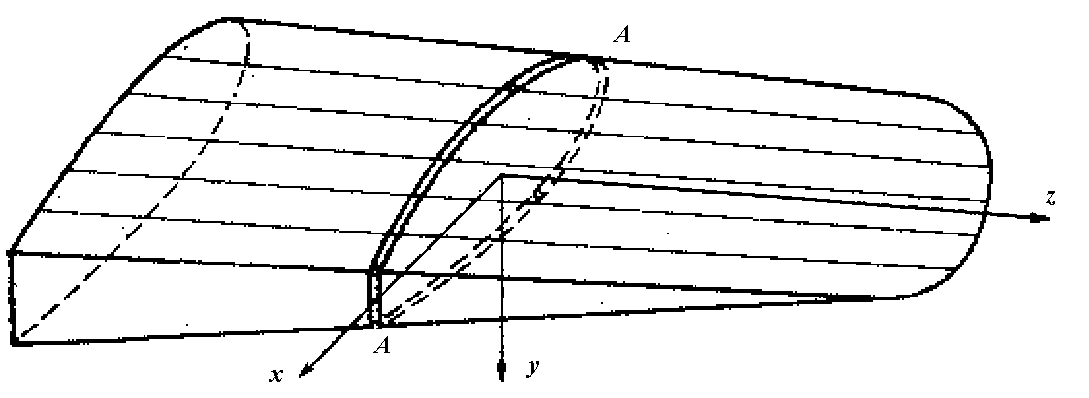 ис. 4.2.

Очевидно, что . При n = m имеем частный случай контурного крепления, при этом нет никаких оснований ожидатьпераспределения усилий между элементами вблизи разреза. При n > m, наоборот, существенное перераспределение усилий более чем очевидно. Рассеченные ребра будут догружать «неразрезанные» ребра в зоне сечения А – А.

Рис. 4.3.

Предположим, что в сечении А – А разреза нет. После выполнения расчета обычными методами получим в продольных ребрах усилия , а в панелях – потоки (рис. 4.3). В сечении А – А данные усилия будут иметь значения и . Данные значения будут удовлетворять уравнениям

; (4.22)

; (4.23)

; (4.24)

; (4.25)

; (4.26)

. (4.27)

Здесь M_0y, M_0x, M_0z, Q_0x и Q_0y – моменты и перерезывающие силы в сечении А – А.

Р ис. 4.4.

В реальной конструкции с разрезом в сечении А – А (рис. 4.4) нагружения будут существенно иными. Обозначим осевые усилия в продольных ребрах и потоки в панелях P_i и q_i, соответственно. В сечении А – А они примут значения P_0i и q_0i. Точно также будут выполнятся уравнения (4.22) – (4.27)

; (4.28)

; (4.29)

; (4.30)

; (4.31)

; (4.34)

. (4.35)

Очевидно, что только в «неразрезных» ребрах с узлами , тогда как в остальных ребрах P_0i=0. Следовательно, сечение А – А будет подвергаться депланированию.

Вычитая уравнения (4.22) – (4.27) из уравнений (4.28) – (4.35) получаем

; (4.36)

; (4.37)

; (4.38)

; (4.39)

; (4.40)

. (4.41)

Обозначив

(4.42)

и

(4.43)

перепишем уравнения (4.36) – (4.41) в следующем виде

; (4.44)

; (4.43)

; (4.45)

; (4.46)

; (4.47)

. (4.48)

Из (4.44) – (4.45) следует, что потоки касательных усилий взаимно уравновешиваются и в сечении действует только набор взаимно уравновешенных осевых сил P_0i.

Обозначим усилия возникающие от данных сил в конструкции как P_i и q_i. Необходимо найти усилия P_0i, после чего определить возникающие от их действия усилия P_i и q_i. После чего эти усилия нужно добавить к усилиям возникающим в крыле без разреза, в чем, собственно, и состоит решение задачи.

Р ис. 4.5.

Поскольку нагружение силами P_0i является локальным, то значительные напряжения в зоне разреза будут быстро затухать при удалении от него. Этопозволяет нам вместо реальной конструкции использовать симметричную относительно разреза бесконечную конструкцию с постоянным сечением.

Известно, что осевое перемещение при депланации вычисляется по формуле (4.21)

(4.49)

Поскольку точки лежащие в плоскости симметрии не могут иметь осевых перемещений, следовательно v_i = 0 и

, (4.50)

где ^*, ^* и ^* неизвестные пока.

Такие уравнения можно записать для всех m соединенных ребер. Суммируя произведения (4.50) на x_i, произведения (4.50) на y_i, а также просто суммируя (4.50) получаем с учетом (4.42) три уравнения

, (4.51)

, (4.52)

. (4.53)

Будем считать, что координаты x_i, y_i взяты относительно главных центральных осей сечения состоящего из m площадей неразрезанных ребер, тогда

, (4.54)

, (4.55)

, (4.56)

, (4.57)

, (4.58)

. (4.59)

Здесь , – моменты инерции площадей неразрезанных ребер в их главных осях, а – суммарная площадь неразрезанных ребер.

Из соотношений (4.28) – (4.30)имеем

; ; .

Поскольку только в m неразрезанных ребрах, то следовательно сумма по m P_0i равна сумме по всем ребрам. С учетом этого, подставляя (4.54) – (4.59), а также (4.28) – (4.30) в (4.51) - (4.53) получаем

, (4.60)

(4.61)

(4.62)

Откуда получаем выражения для вычисления где ^*, ^* и ^*

, (4.63)

, (4.64)

. (4.65)

Зная значения где ^*, ^* и ^* по формуле (4.50) можно получить значения P_0i для m неразрезанных ребер. Посколько для остальных (n – m) ребер P_0i = 0, то из формулы (4.42) следует, что для них .

Таким образом, мы получили дополнительное нагружение от наличия разреза в сечении крыла.

, (4.66)

. (4.67)

Суммируя усилия от наличия разреза с нагружением конструкции без разреза получаем суммарное нагружение конструкции

, (4.68)

. (4.69)

Таким образом, последовательность расчета в зоне разреза следующая:

1. Методами, описанными в разделах 3.6 и 3.7, получаем усилия и потоки касательных напряжений для условно неразрезанной конструкции.

2. Вычисляем суммарную площадь неразрезанных ребер, а также суммарные моменты инерции и неразрезанных ребер относительно центральных главных осей сечения образованного неразрезанными ребрами.

3. По формуле (4.50) вычисляем значения дополнительных усилий в ребрах P_0i.

4. По формулам (4.66) и (4.67) вычисляем дополнительные усилия в зоне разреза.

5. По формулам (4.68) и (4.69) вычисляем суммарное нагружение в зоне разреза.