
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Если предел последовательности существует, то он единственен, т.Е. Если и если , то
- •Если предел функции имеет при существует, то он единственен, т.Е. , , то
- •Теорема 8.3 (Свойства бесконечно малых)
- •Бесконечно малые последовательности обладают вполне аналогичными свойствами:
- •Замечание: строгое неравенство между функциями может не сохраниться для пределов.
- •Доказательство
- •Теорема 9.5 (первый замечательный предел)
- •Доказательство
- •Вопрос 10: предел монотонной ограниченной функции
- •Теорема 10.1 (к. Вейерштрасс)
- •Теорема 10.2 (к. Вейерштрасс)
- •Вопрос 11: число e Теорема 11.1 Существует предел последовательности .
- •Теорема 11.2 Имеет место равенство
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •◄Необходимость
- •Достаточность
- •◄Необходимость
- •Достаточность
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •Пример второй ситуации более простой. Пусть
- •Определение 13.4. Точкой разрыва первого рода называется точка ,
- •Вопрос 14: непрерывность элементарных функций
- •4. Непрерывность логарифмической функции
- •Вопрос 15: символы , . Вычисление , ,
- •Примеры.
- •Теорема 15.2. , т.Е.
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Полученное противоречие доказывает теорему.
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •Теорема 19.1. Функция , дифференцируемая в точке , непрерывна в этой точке.
- •2.Производная
- •◄Действительно,
- •Пример 3'. Модуль не имеет производной в точке 0.
- •Предельные величины.
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •Положив в формуле (1) , получим
- •Таким образом, мы видим, что
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вторая производная функции , заданной параметрически
- •5.Дифференциалы высших порядков.
- •Напомним, что если функция дифференцируема в точке , то
- •Эластичность и её свойства.
- •Если предположить, что X , то можно рассматривать величину
- •В качестве примера рассмотрим ценовую эластичность спроса.
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •В качестве примера рассмотрите и
- •Из условий следует, что
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •Противоположное неравенство
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Зафиксировав , рассмотрим функцию от переменной вида
- •Поэтому
- •Вопрос 35.
- •Поэтому выражение (20.3) можно заменить на
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Здесь мы воспользовались тем, что .Например, при
- •Вопрос 41. Формулы Тейлора.
- •В случае точки минимума
Вопрос 1: множества и операции над ними
Понятие множества
Понятия множества и его элемента относятся к числу первичных, неопределяемых понятий математики. К таким же понятиям относятся точки, прямая линия и др. Создатель теории множеств Георг Кантор в 1872 году описал понятие множества, как « объединения в одно целое объектов, хорошо различаемых нашей интуицией или нашей мыслью».
Мы будем говорить, что определено некоторое множество
 объектов,
если указан признак, который позволяет
относительно каждого предмета
объектов,
если указан признак, который позволяет
относительно каждого предмета
 сказать, принадлежит ли этот предмет
множеству
,
или нет.
сказать, принадлежит ли этот предмет
множеству
,
или нет.Элементы множеств в дальнейшем будем записывать строчными латинскими буквами, сами множества – прописными. Обозначение
 используется, как краткая запись
утверждения:
используется, как краткая запись
утверждения:
 есть
элемент множества
есть
элемент множества
 ,
или:
принадлежит
.
Аналогично, обозначение
,
или:
принадлежит
.
Аналогично, обозначение
 используется, как краткая запись
утверждения:
не
является элементом множества
,
или:
не принадлежит
.
Множество, не имеющее элементов,
называется пустым
и
обозначается
используется, как краткая запись
утверждения:
не
является элементом множества
,
или:
не принадлежит
.
Множество, не имеющее элементов,
называется пустым
и
обозначается
 .
.Укажем ряд способов задания множеств. Во-первых, можно просто перечислить все элементы множества, если этих элементов – конечное число, т.е. если множество конечное. Например, множество, состоящее из двух чисел, 0 и 1. В этом случае используется обозначение {0,1}. Для произвольного конечного множества, например, состоящего из различных элементов
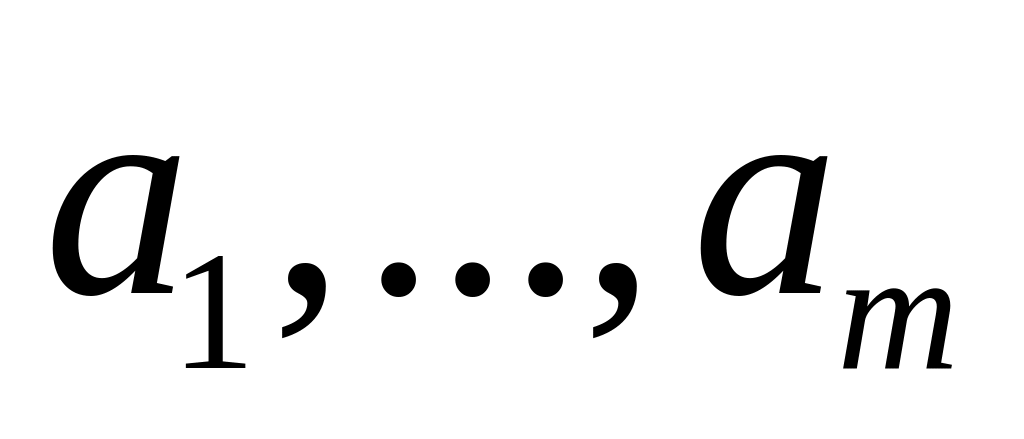 ,
используется обозначение
,
используется обозначение
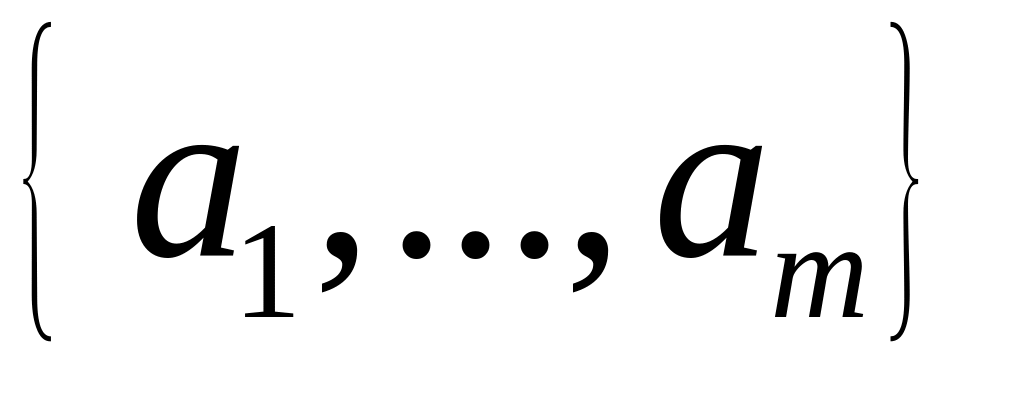 .
Подчеркнём, что в этом обозначении
множества элементы
должны быть различными, однако они
могут быть перечислены в произвольном
порядке, например,
.
Подчеркнём, что в этом обозначении
множества элементы
должны быть различными, однако они
могут быть перечислены в произвольном
порядке, например,
 и
и
 - различные обозначения одного и того
же множества.
- различные обозначения одного и того
же множества.
Можно также указать свойство, которому удовлетворяют элементы рассматриваемого множества. Например, множество действительных чисел, больших 5. Обозначим его
 .
.
Некоторые множества определяются с помощью указания способа последовательного построения его элементов. Например,
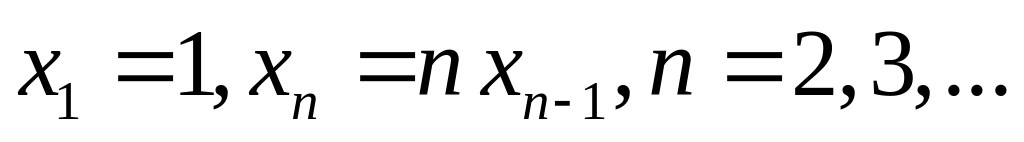 .
.Новые множества можно получать и в результате операций над заданными множествами.
Наиболее часто у нас будут рассматриваться множество R действительных чисел, множество N натуральных чисел, множество Z целых чисел, множество Q рациональных чисел.
Подмножества
Важный способ задания множества – выделение его, как части некоторого основного множества. Основное множество образуется всеми элементами какого-нибудь определённого типа. Например, множество целых чисел, множество простых чисел и т.п.
В качестве примера рассмотрим основное множество целых чисел и выберем в нём те числа, которые делятся на 2, т.е. чётные числа. Мы получили множество чётных чисел, которое является подмножеством основного множества целых чисел.
В общем случае, если все элементы множества являются также элементами множества
 ,
то мы говорим, что
есть подмножество
,
или
включено в
,
и обозначаем это так:
,
то мы говорим, что
есть подмножество
,
или
включено в
,
и обозначаем это так:
 .
.Если оказалось, что одновременно и
 ,
то эти множества называются равными,
что обозначается
,
то эти множества называются равными,
что обозначается
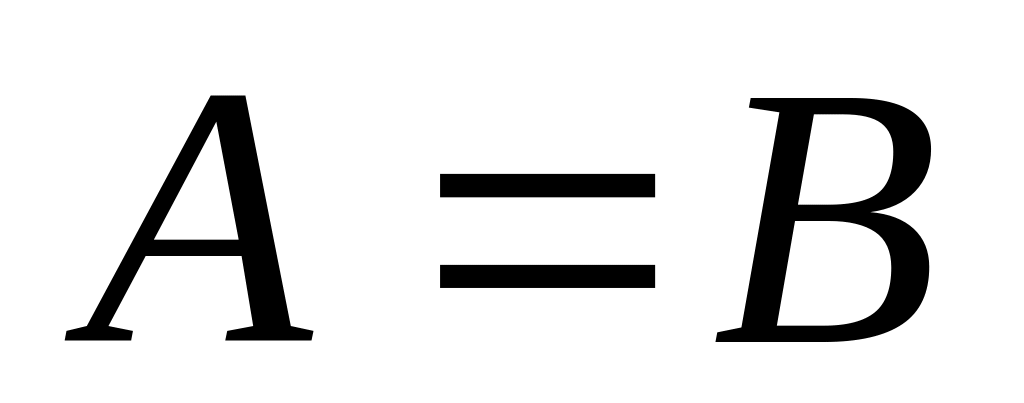 .
Проще говоря, равные множества состоят
из одних и тех же элементов.
.
Проще говоря, равные множества состоят
из одних и тех же элементов.Из того, что и
 следует, что
(т.е. отношение включения множеств
является транзитивным.
Понятие отношения и его свойства будут
подробнее описаны в билете 2).
следует, что
(т.е. отношение включения множеств
является транзитивным.
Понятие отношения и его свойства будут
подробнее описаны в билете 2).Операции над множествами
Пусть задано некоторое основное множество и его подмножества и .
Определение 1.1.Объединение
 этих
множеств определяется, как подмножество
множества
,
состоящее из элементов, входящих хотя
бы в одно из множеств
и
.
этих
множеств определяется, как подмножество
множества
,
состоящее из элементов, входящих хотя
бы в одно из множеств
и
.Определение 1.2.Пересечение
 этих
множеств определяется, как подмножество
множества
,
состоящее из элементов, одновременно
входящих как в множество
,
так и в множество
.
этих
множеств определяется, как подмножество
множества
,
состоящее из элементов, одновременно
входящих как в множество
,
так и в множество
.Определение 1.3Дополнение
 множества
определяется, как подмножество множества
,
не содержащее элементов множества
.
множества
определяется, как подмножество множества
,
не содержащее элементов множества
.
Перечислим некоторые свойства операций над множествами.

В качестве примера докажем свойство
 .
Для этого заметим, что условие
.
Для этого заметим, что условие
 равносильно тому, что
равносильно тому, что
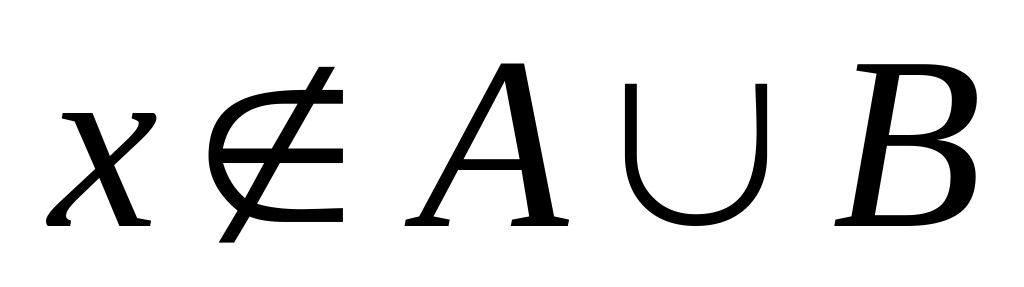 .
Это, в свою очередь, равносильно тому,
что
.
Это, в свою очередь, равносильно тому,
что
 и
и
 ,
т.е.
,
т.е. .
Свойство доказано.
.
Свойство доказано.Это утверждение, вместе с утверждением
 ,
называют теоремами
де Моргана.
Доказательства остальных свойств ещё
проще и мы их опускаем.
,
называют теоремами
де Моргана.
Доказательства остальных свойств ещё
проще и мы их опускаем.Подмножества основного множества вместе с введёнными выше операциями, дают пример так называемой булевой алгебры.
Вопрос 2 : декартово произведение множеств, бинарные отношения
Декартово произведение множеств
Определение 2.1.Пусть даны два множества , и . Образуем множество упорядоченных пар элементов, у которых первый элемент принадлежит , а второй - . Полученное множество называется декартовым произведением множеств и и обозначается
 .
.
Перечислим некоторые простейшие свойства декартова произведения.
Если
 ,
то
,
то
 ;
;
 .
.Отметим, что
 тогда и только тогда, когда
тогда и только тогда, когда
 .
.Бинарные отношения
Определение 2.2.Любое подмножество
 множества
называется бинарным
отношением.
множества
называется бинарным
отношением.Аналогичным образом можно рассматривать декартовы произведения трёх и более множеств. Их подмножества будут называться тернарными и т.п. отношениями.
Изучим понятие бинарного отношения более подробно, так как оно является важным не только для математического анализа, но и для компьютерной математики.
Задавать бинарные соотношения конечных множеств можно, например, с помощью таблиц. Например, пусть
 .
Зададим отношение
.
Зададим отношение
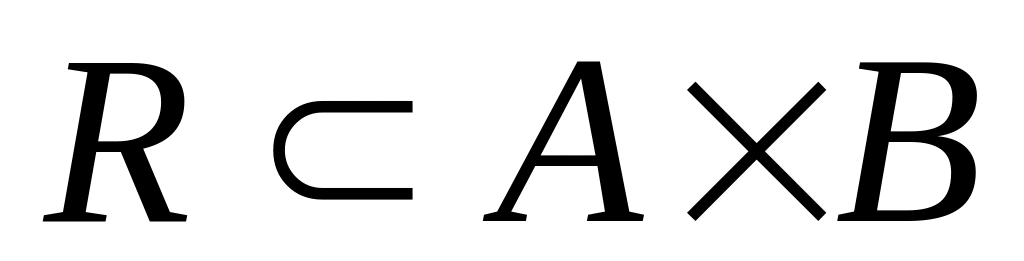 свойством: пара
свойством: пара
 принадлежит отношению
тогда и только тогда, когда
есть делитель
принадлежит отношению
тогда и только тогда, когда
есть делитель
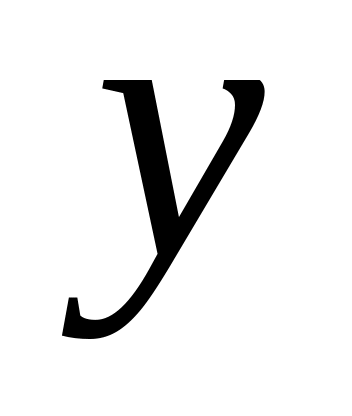 .
Отношение
,
таким образом, состоит из пар:
.
Отношение
,
таким образом, состоит из пар:

Изобразим это отношение следующим образом. Проведём три прямые, соответствующие трём элементам множества . Проведём шесть перпендикулярных им прямых, соответствующих элементам множества . Отметим жирной точкой те точки пересечения этих прямых, которые соответствуют отношению .(рис.1)

Рис.1 Рис.2 Рис.3
Другой способ задания бинарного отношения – использование стрелок. Элементы и изображаются в виде точек плоскости. Стрелками соединены те и только те элементы
 ,
для которых
,
для которых
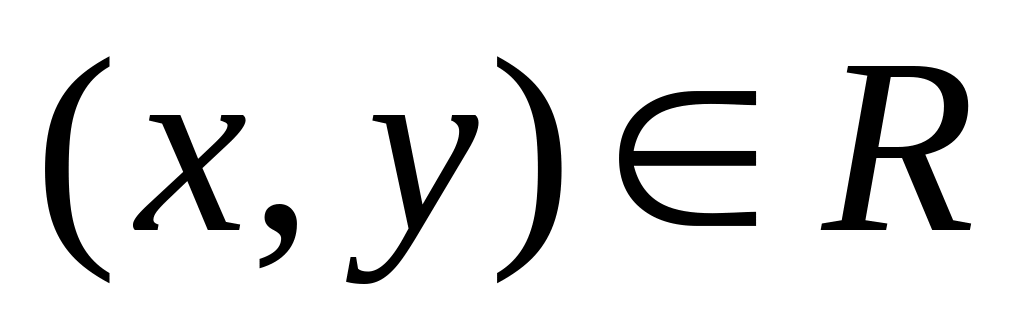 .(рис.2)
.(рис.2)Это же бинарное отношение можно задать матрицей, состоящей из 0 и 1. Её строки соответствуют элементам множества
 ,
столбцы – элементам множества
,
столбцы – элементам множества
 .
Элемент этой матрицы равен 1 тогда и
только тогда, когда он стоит на пересечении
строки и столбца, соответствующих паре
,
для которой
.
.
Элемент этой матрицы равен 1 тогда и
только тогда, когда он стоит на пересечении
строки и столбца, соответствующих паре
,
для которой
.Определение 2.3.Элемент называется проекцией элемента
 на множество
.
Для произвольного подмножества
на множество
.
Для произвольного подмножества
 его проекцией
на
называется множество, состоящее из
проекций на
всех элементов множества
его проекцией
на
называется множество, состоящее из
проекций на
всех элементов множества
 .
.Определение 2.4. Сечением
 множества
называется множество
множества
называется множество
 элементов
элементов
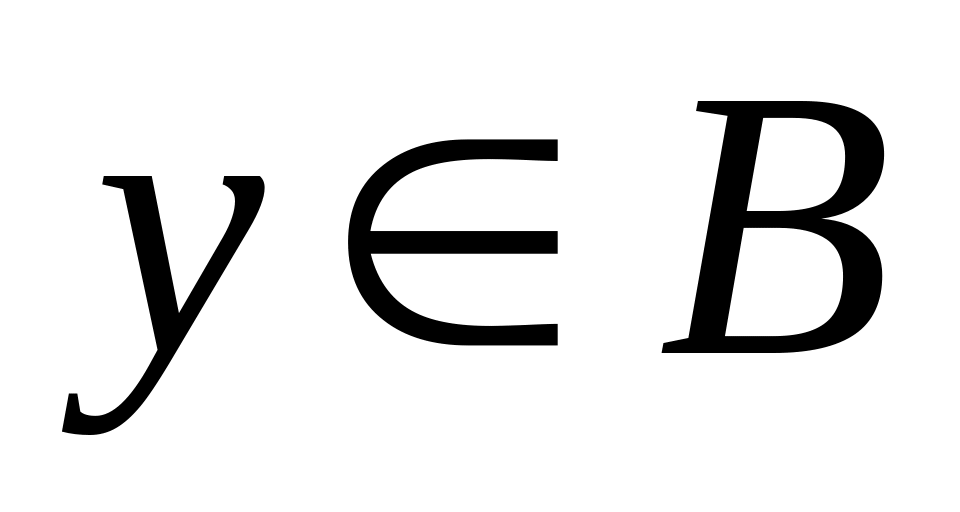 ,
для которых
,
для которых
 .
Множество сечений отношения
называется фактормножеством
по отношению
и обозначается
.
Множество сечений отношения
называется фактормножеством
по отношению
и обозначается
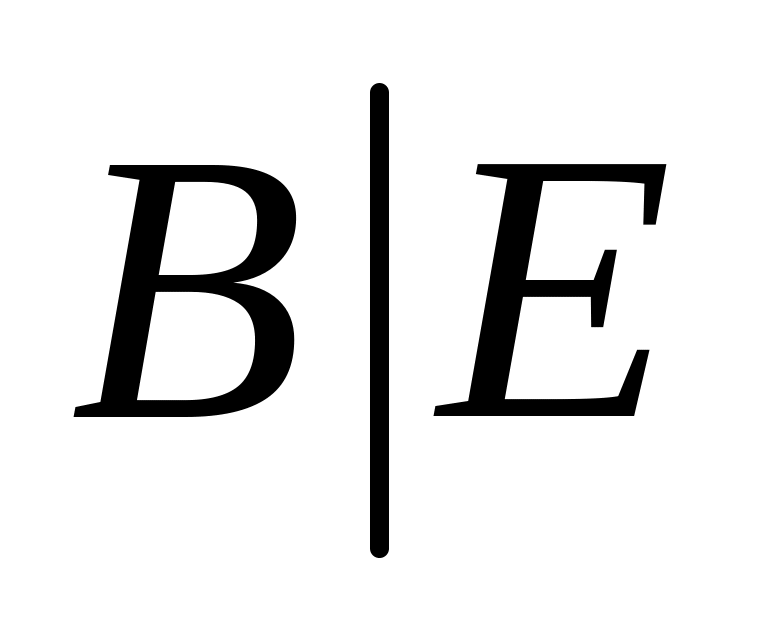 .
.Так как отношения представляют собой множества, к ним можно применить операции, определённые в предыдущем параграфе. Но кроме этих операций есть ещё важные операции композиции и симметризации.
Пусть даны множества
 и отношения
и отношения
 .
.
Определение 2.5.Композиция отношений
 - это отношение
- это отношение
 между элементами множеств
и
между элементами множеств
и
 такое, что для всех
такое, что для всех
 сечение множества
по
совпадает с сечением множества
сечение множества
по
совпадает с сечением множества
 по подмножеству
по подмножеству
 ,
т.е.
,
т.е.
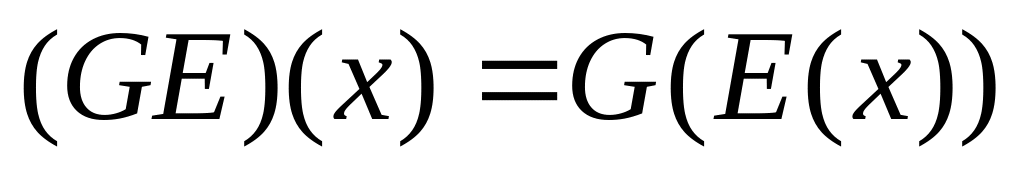 .
.
Если даны две пары отношений ,
 и
и
 ,
причём
,
причём
 и
и
 ,
то операция композиции обладает
следующим свойством:
,
то операция композиции обладает
следующим свойством:
 .
.Определение 2.6.Отношение, симметричное к некоторому отношению и обозначаемое
 ,
представляет собой подмножество
множества
,
представляет собой подмножество
множества
 ,
образованное теми парами
,
образованное теми парами
 ,
для которых
,
для которых
 .
Если
и
.
Если
и
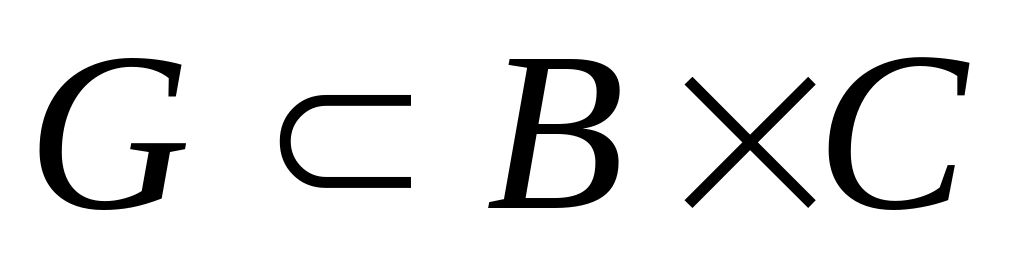 ,
то
,
то
 .
.Предположим, что задано некоторое основное множество . Отношение
 называется отношением
эквивалентности,
если оно обладает такими свойствами:
называется отношением
эквивалентности,
если оно обладает такими свойствами:1. Рефлексивностью: всякий элемент эквивалентен самому себе. Иными словами, для любого
 пара
пара
 .
.2. Симметричностью: для любых двух элементов
 из того, что
эквивалентен
из того, что
эквивалентен
 следует, что
эквивалентен
.
Другими словами, если
следует, что
эквивалентен
.
Другими словами, если
 ,
то
,
то
 .
Это означает, что отношение
совпадает со своим обратным,
.
.
Это означает, что отношение
совпадает со своим обратным,
.3. Транзитивностью: если эквивалентен , а эквивалентен
 ,
то
эквивалентен
.
Иначе говоря, если
и
,
то
эквивалентен
.
Иначе говоря, если
и
 ,
то
,
то
 .
.Очень часто отношение эквивалентности элементов обозначается так:
 .
.Важным понятием является понятие класса эквивалентности. Класс эквивалентности элемента состоит из всех элементов
 ,
эквивалентных элементу
.
Для неэквивалентных элементов их
классы эквивалентности не пересекаются.
Множество классов эквивалентности
называется фактормножеством
множества
по отношению
и обозначается
,
эквивалентных элементу
.
Для неэквивалентных элементов их
классы эквивалентности не пересекаются.
Множество классов эквивалентности
называется фактормножеством
множества
по отношению
и обозначается
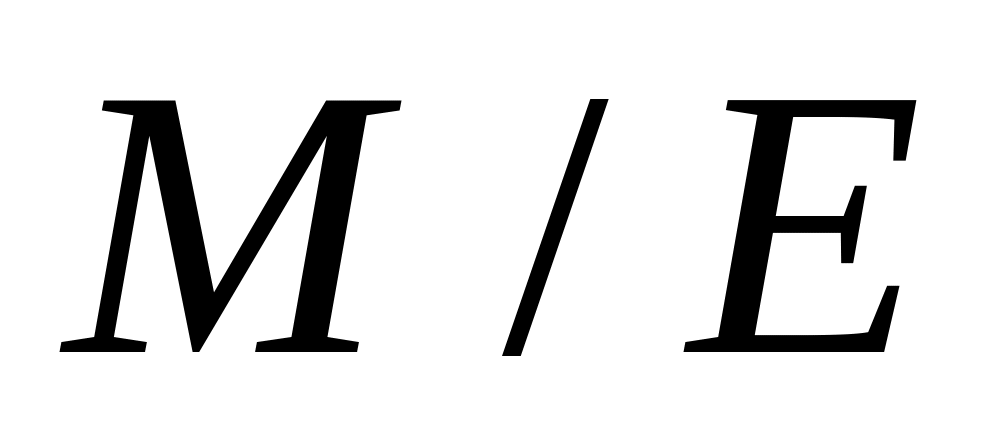 .
Если взять ровно по одному элементу из
каждого класса эквивалентности, получим
систему
представителей.
.
Если взять ровно по одному элементу из
каждого класса эквивалентности, получим
систему
представителей.
В качестве примера рассмотрим множество Z целых чисел. Зафиксируем произвольное целое число
 и назовём два целых числа
и назовём два целых числа
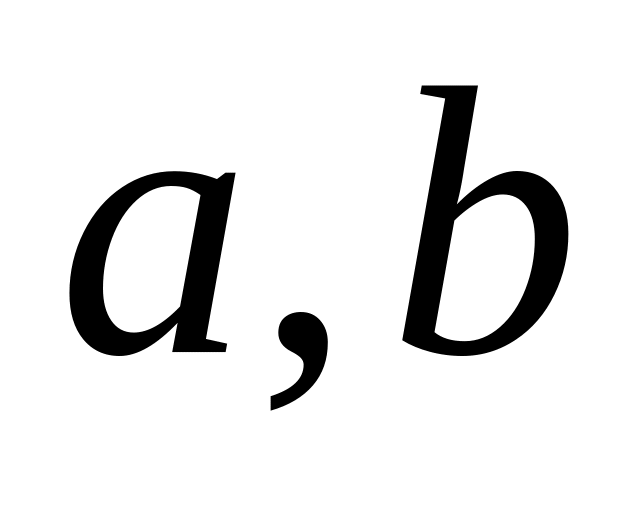 сравнимыми
по модулю
сравнимыми
по модулю
 (что
обозначается
(что
обозначается
 ),
если разность
),
если разность
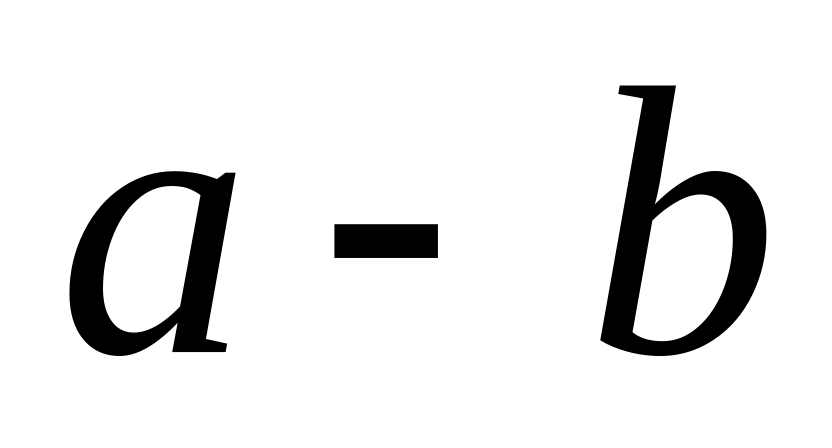 делится на
.
Легко видеть, определённое таким образом
отношение обладает всеми свойствами
отношения эквивалентности. Классы
эквивалентности называются классами
вычетов по модулю
,
в качестве системы представителей
можно взять всевозможные остатки от
деления на
,
т.е. числа
делится на
.
Легко видеть, определённое таким образом
отношение обладает всеми свойствами
отношения эквивалентности. Классы
эквивалентности называются классами
вычетов по модулю
,
в качестве системы представителей
можно взять всевозможные остатки от
деления на
,
т.е. числа
 .
Это множество обозначается Z
.
Это множество обозначается Z
 .
На нём можно определить операции
сложения и умножения естественным
образом. Имеется в виду, что следует
просуммировать вычеты, как обычные
целые числа, разделить сумму на
с остатком и этот остаток назвать суммой
вычетов. Аналогично определим произведение
вычетов.
.
На нём можно определить операции
сложения и умножения естественным
образом. Имеется в виду, что следует
просуммировать вычеты, как обычные
целые числа, разделить сумму на
с остатком и этот остаток назвать суммой
вычетов. Аналогично определим произведение
вычетов.
Вопрос 3: отображения и их свойства
Определение 3.1.Назовём бинарное отношение функциональным, если для каждого сечение
 содержит не более одного элемента.
содержит не более одного элемента.
Определение 3.2.Если отношение , симметричное к отношению , также является функциональным, то отношение называется взаимно однозначным.
Определение 3.3.Если для каждого сечение содержит ровно один элемент, то функциональное отношение всюду определено.
С функциональным отношением непосредственно связано понятие отображения.
Определение 3.4.Отображение, обозначим его
 ,
сопоставляет каждому элементу,
называемому аргументом
отображения,
для которого сечение
- непустое множество, единственный
элемент
,
сопоставляет каждому элементу,
называемому аргументом
отображения,
для которого сечение
- непустое множество, единственный
элемент
 подмножества
множества
.
Этот элемент
называется образом
элемента
при отображении
.
подмножества
множества
.
Этот элемент
называется образом
элемента
при отображении
.
Множество тех элементов , для которых существует , называется областью определения отображения .
Определение 3.5.Если отображение определено на всём множестве , то говорят, что задано отображение в .
Определение 3.6.Множество образов элементов при отображении называется образом отображения. Если
 ,
то образ
,
то образ
 определяется,
как множество образов элементов
определяется,
как множество образов элементов
 .
.Определение 3.7.Если образ совпадает со всем множеством , то говорят, что задано отображение на , или что - сюръективное отображение, или сюръекция. (При этом требование всюду определённости не является обязательным).
Определение 3.8.Если
 ,
то
,
то
 обозначает прообраз
множества
,
т.е. множество тех элементов
,
для которых
обозначает прообраз
множества
,
т.е. множество тех элементов
,
для которых
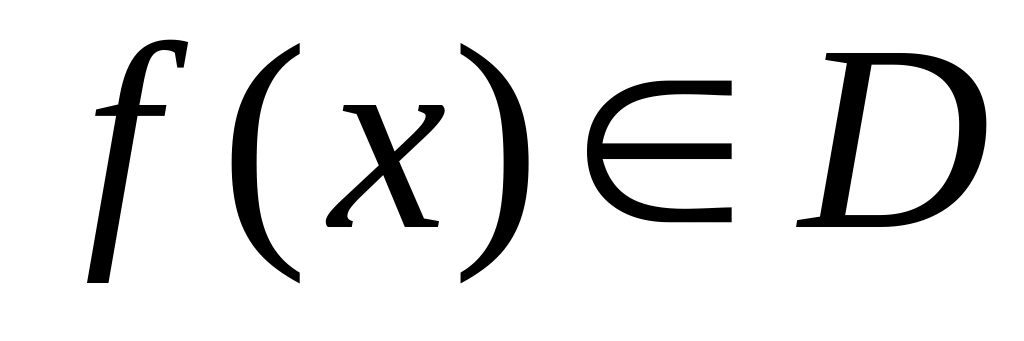 .
.
Отметим очевидные свойства образа и прообраза:
 .
.Определение 3.9.Если отношение является взаимно однозначным, то отображение, соответствующее , называется обратным к и обозначается
 .
Если при этом отношение
всюду определено, то
называется инъективным
отображением,
или инъекцией.
Если, кроме того, отображение ещё и
сюръективно, то оно называется биективным
или биекцией.
.
Если при этом отношение
всюду определено, то
называется инъективным
отображением,
или инъекцией.
Если, кроме того, отображение ещё и
сюръективно, то оно называется биективным
или биекцией.Отметим, что выше мы использовали обозначение прообраза и в случаях, когда обратное к отображение не существует. Если же обратное отображение существует, то прообраз можно рассматривать, как образ множества
 при отображении
.
при отображении
.Наиболее часто встречающимся функциональным отношением является обычная функция
 ,
определённая на некотором подмножестве
,
определённая на некотором подмножестве
 числовой прямой, значения которой
образуют множество
числовой прямой, значения которой
образуют множество
 .
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве
.
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве
 ,
в которое входят те пары
,
в которое входят те пары
 ,
для которых выполнено равенство
.
Изображение этого множества пар на
плоскости носит название графика
функции.
,
для которых выполнено равенство
.
Изображение этого множества пар на
плоскости носит название графика
функции.
Вопрос 4: множество действительных чисел. Аксиома отделимости
Предварительные сведения о натуральных, целых, рациональных числах. На экзамене содержание параграфов 1,2,3 следует знать, но можно не рассказывать. (Содержание параграфа 1΄ можно и не знать, сведения об аксиоматике Пеано приведены исключительно для общего развития).
