18.Показатели относительного рассеивания.

Коэффициент осцилляции К₀ отражает относительные колебания крайних значений признака вокруг средней:

.

Относительное линейное отклонение K_d характеризует долю усреднённого значения абсолютных отклонений от средней величины.

.

Коэффициент вариации  определяют по формуле:

.

Коэффициент вариации измеряет рассеивание данных относительно среднего значения. Измеряется в %, а не в единицах измерения исходных данных.

Коэффициент вариации позволяет сравнить две выборки, элементы которых выражаются в разных единицах измерения.

Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние (серединные) характеристики достаточно надежно характеризуют совокупность по варьирующему признаку, когда относительные показатели вариации больше 35% - то ненадежно. В этом случае варианты ряда распределения существенно отличаются от средних характеристик.

19.Виды дисперсии.

Виды дисперсии – это показатель изменения признака в совокупности.

Определим три вида дисперсии:

1. общую дисперсию ,

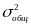2. межгрупповую дисперсию ,

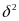3. среднюю внутригрупповых дисперсий .

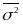Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности.

где - общая средняя для всей изучаемой совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки.

где - средняя по отдельным группам;

- средняя общая;

- численность отдельных групп.

Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Это вариация результативного признака, которая возникает под влиянием всех остальных факторов, кроме группировочного.

где - дисперсия в каждой группе.

Большую практическую значимость имеет правило сложения дисперсий:

.

Коэффициент детерминации ² находят по формуле: .

Он характеризует долю вариации группировочного признака в общем объеме вариации или на сколько процентов уровень результативного признака определяется группировочным признаком.

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.

Это отношение характеризует тесноту связи между признаками, т.е. близость корреляционной (неполной) зависимости к функциональной (полной). Этот показатель изменяется от нуля до единицы. Точность его зависит от размеров совокупности: чем больше совокупность, тем он надежнее. Недостатки эмпирического корреляционного отношения: невозможность определить направление связи (прямая зависимость или обратная); невозможность определения формы связи.

Применение понятий

Распределение служащих двух отделов крупного предприятия по уровню зарплаты следующее:

№	Уровень зарплаты, у.е.	Число служащих
		отдел 1	отдел 2	Всего
1.	до 100	4	8	12
2.	100 - 105	40	62	102
3.	105 - 110	28	30	58
4.	110 - 115	15	12	27
5.	115	13	8	21
Итого		100	120	220

Определить:

- среднюю зарплату по каждому отделу и предприятию в целом;

- дисперсию для каждого отдела;

- среднюю внутригрупповых дисперсий;

- межгрупповую дисперсию;

- общую дисперсию.

Решение:

Отдел 1.

,

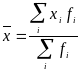у.е.

Отдел 2.

у.е.

Предприятие:

у.е.

Дисперсию по каждому отделу определяем по формуле:

,

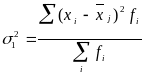j = 1, 2

i = 1, 2, 3, 4, 5

, . Аналогично для второго отдела.

Средняя внутригрупповая дисперсия:

.

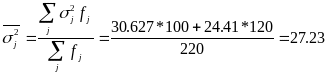Межгрупповая дисперсия:

.

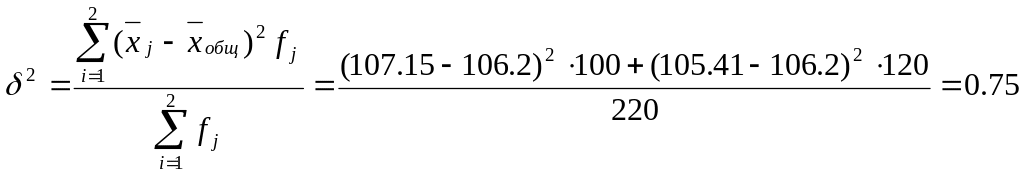Общая дисперсия:

.

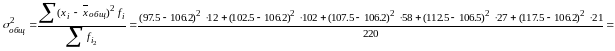
Проверка по правилу сложения дисперсий:

.

Коэффициент (индекс) детерминации: =0,75/27,98*100=2,7%.

Вывод. Распределение служащих по отделам на 2,7% определяется уровнем заработной платы и на 97,3% всеми остальными факторами.

Эмпирическое корреляционное отношение будет равно:

.

Вывод. Полученное значение свидетельствует о достаточно слабой связи между признаками, не приближающейся к функциональной зависимости.