16.Структурные средние величины.

Для характеристики структуры совокупности применяют структурные средние. К таким показателям относятся мода и медиана.

Мода - величина признака, которая встречается в изучаемом ряду, или в совокупности, чаще всего. Мода широко используется в коммерческой практике при изучении покупательского спроса, при регистрации цен и т.д. В дискретном ряду мода - это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту:

где x_нmo - нижняя граница модального интервала;

i_mo - величина модального интервала;

f_mo - частота, соответствующая модальному интервалу;

f_mo-1, f_mo+1 - частоты интервалов, предшествующих и следующих за модальным интервалом.

Медиана - это величина, которая делит численность упорядоченного вариационного ряда на две равные части. Для упорядоченного дискретного ряда с нечетным числом значений – медиана – это серединный элемент ряда. Для упорядоченного дискретного ряда с четным числом значений – медиана – это среднее арифметическое двух серединных элементов ряда.

Для интервального ряда медианный - это интервал, для которого накопленная частота больше или равна полусуммы частот ряда. Для интервального ряда медиана находится по формуле:

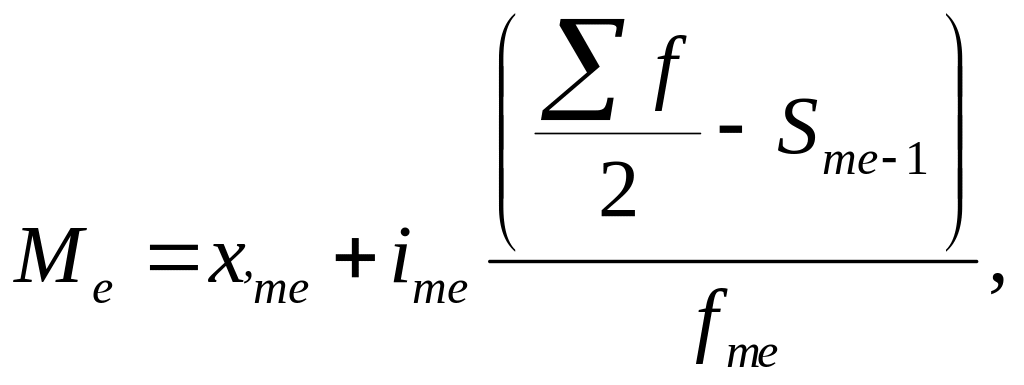
где x_нme - нижняя граница медианного интервала;

i_me - величина медианного интервала;

 f/2 - полусумма частот ряда;

S_me-1 - сумма накопленных частот, предшествующих медианному интервалу;

f_me - частота медианного интервала.

№

Зарплата, у.е.

Численность

	90 - 100	10
	100 - 110	14
	110 - 120	28
	120 - 130	22
	130 - 140	15

Итого

89

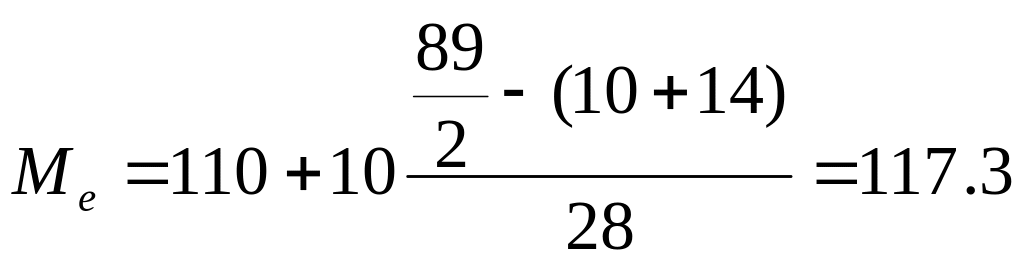у.е. у.е.

Сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая:

.

Это особое свойство медианы находит широкое применение в маркетинговой деятельности.

Если среднее арифметическое значение, мода и медиана совпадают, то такая группа данных симметрична.

Величины, находящиеся на одной, двух и трёх четвертях расстояния от начала ряда называются квартилями, на одной десятой - децилями, на одной сотой - процентилями.

Децилем называется структурная величина, которая делит распределение на 10 равных частей по 10% единиц или объемов в каждой части. Децилей девять, децильных групп – десять.

17.Понятие вариации. Абсолютные и средние показатели вариации.

Различие (степень колебания) отдельных значений характеризуют показатели вариации.

Вариация – количественное изменение величины исследуемого признака в пределах однородной совокупности, которое обусловлено перекрещивающимся влиянием действия различных факторов.

Степень близости данных отдельных единиц х_i к средней измеряется рядом абсолютных, средних и относительных показателей.

Абсолютные показатели вариации

Размах вариации R - это разность между наибольшим и наименьшим значением вариантов.

.

Размах позволяет измерить общий разброс данных. Его слабость в том, что он никак не учитывает, как именно распределены данные между минимальным и максимальным элементами.

Межквартильный размах (средний размах) – это разность между третьим и первым квартилями выборки.

, где Q₁ = (n+1)/4 Q₃ = 3(n+1)/4

Эта величина позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов.

Применение понятий.

Межквартильный размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, вычислим, используя следующий упорядоченный массив

-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5

Эта величина характеризует размах половины выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с высоким уровнем риска. Интервал, ограниченный числами 9,8 и -0,7 часто называют средней половиной.

Суммарные количественные характеристики, такие как медиана, первый и третий квартили, межквартильный размах, на которые не влияют выбросы, называются устойчивыми показателями.

Размах и межквартильный размах позволяют оценить общий и средний разброс значений, но они не учитывают как именно распределены данные. Дисперсия и стандартное (среднеквадратическое) отклонение лишены этого недостатка.

Средние показатели вариации

Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учёта знака этих отклонений

.

Дисперсия ² (средний квадрат отклонений) определяется по формуле:

,

Чем меньше дисперсия, тем лучше средняя арифметическая отражает собой всю представленную совокупность.

Среднее квадратическое отклонение  может быть найдено таким образом:

.

Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить степень колебания данных вокруг среднего значения.

Интерпретация понятий

Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить разброс данных вокруг среднего значения, т.е. сколько элементов выборки меньше среднего, а сколько – больше. Дисперсия обладает ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения (квадратный %, квадратный доллар и т.д.). Поэтому естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерения - %, доллары …

Стандартное отклонение позволяет оценить величину колебания значений вокруг среднего значения. Практически во всех ситуациях наблюдаемые величины лежат в интервале плюс-минус одно стандартное отклонение от среднего значения. Поэтому, зная среднее арифметическое и среднее квадратическое (стандартное) отклонение можно определить интервал, которому принадлежит основная масса данных.