37.Агрегатные индексы.

Происходят от латинского слова «aggrega» - присоединяю. В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых статистических совокупностей:

Индексируемая величина * Соизмеритель

изменяется в числителе для перехода к однородным

и знаменателе показателям – неизменен

Общий индекс цен, если соизмеритель q₁ - данные о количестве реализации товаров в текущем периоде, это индекс Пааше:

. (3)

Общий индекс цен, если соизмеритель q₀, называется индексом Ласпейреса:

. (4)

Формулы (3) и (4) определяют агрегатные индексы, т.е. индексы в числителе и знаменателе которых находятся произведения индексируемой величины на соизмеритель.

Эти формулы могут быть распространены на индексы других качественных показателей:- себестоимости I_z ,- производительности труда I_t и т.д.

Агрегатные индексы можно определить для физического объёма товарной массы q:

- в ценах базисного периода p₀

, (5)

- в ценах текущего периода p₁

. (6)

При индексном методе анализа коммерческой деятельности надо учитывать, что факторы, влияющие на объем товарооборота – количество реализации и их цены действуют одновременно. В анализе важно определить общий результат их совокупного взаимодействия.

Из формул (3) ... (5) строится общий индекс товарооборота

(7)

В этом индексе производится сравнение двух качественно однородных величин (стоимостей)

38. Средние индексы.

а) При синтезировании общего индекса цен вместо фактического количества товаров (в отчетный или базисный периоды) в качестве соизмерителя могут применяться средние величины реализации товаров за два или большее количество периодов. Примером такого среднего индекса является индекс Лоу (8)

Здесь - среднее количество товаров, реализованных за анализируемый период. Если есть только два периода – базисный и текущий, то средняя величина определяется по формуле средней невзвешенной.

б) Для определения сводных обобщающих показателей изменения розничных цен в коммерческой деятельности используется средняя гармоническая форма общего индекса цен: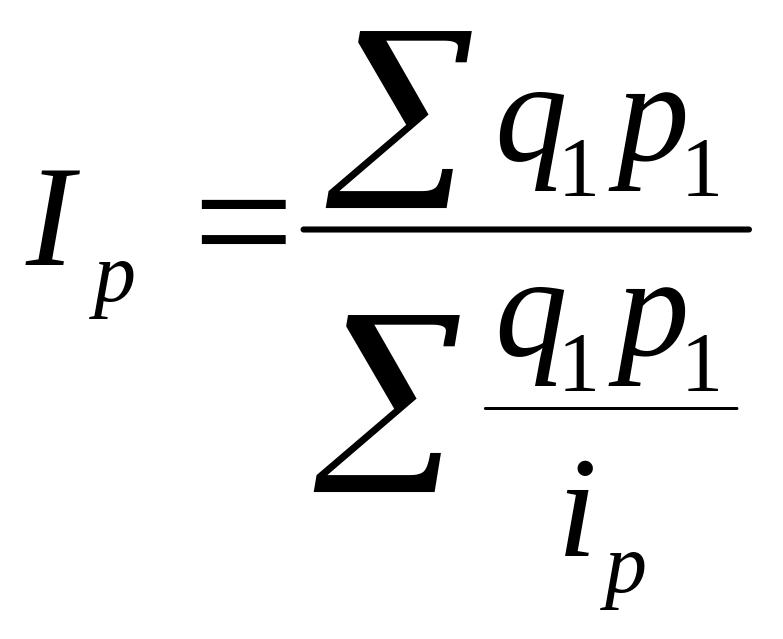 (9)

здесь i_p =р₁/р₀ - индивидуальные (однотоварные) индексы цен.

в) При наличии информации об индивидуальных индексах физического объема и стоимости, реализованных в базисном периоде товаров, общий индекс физического объема может исчисляться по формуле среднего арифметического индекса:

(10)

здесь i_q =q₁/q₀ - индивидуальные индексы физического объема.

39. Применение индексов для изучения структурных сдвигов

Для общего индекса товарооборота выполняется следующая формула:I_qp=I_q*I_p. Эта формула отражает взаимосвязь индекса физического объёма и индекса цен.

Эта формула м.б. использована лишь при условии, что веса-соизмерители в индексах физического объема и цен берутся на разных уровнях. При анализе компонентной зависимости используется формула: Взаимосвязанные индексы могут быть применимы для изучения влияния структурных сдвигов. В таком анализе индексы находятся во взаимосвязи со средними величинами. Из формулы средней арифметической: Следует, что на среднюю величину влияют: индивидуальные значения усредняемого признака; численность отдельных вариантов изучаемой совокупности (их частота). Нам важно определить, в какой мере изменения отдельных вариантов и их частот влияют на изменение средней величины. Это выполнимо с помощью следующей системы взаимосвязанных индексов.

Определим индекс изменения средней величины как произведение индекса в неизменной структуре на индекс, отображающий влияние изменения структуры явления на динамику средней величины .: . (14)

В этой формуле: 1) (15) Это индекс переменного состава (т.к. веса-соизмерители в нем это состав продукции (товаров) текущего f₁ и базисного f₀ периодов). 2) (16). Это индекс постоянного (фиксированного) состава (т.к. веса-соизмерители в нем это состав продукции (товаров) текущего f₁ периода).

3) . Это индекс, отображающий влияние структурных сдвигов на изучаемый показатель (т.к. в нем изменяются только веса-соизмерители).