Тема 9_2011-2012. Статистическое изучение динамики социально-экономических явлений

Вопросы:

1. Понятие о статистических рядах динамики.

2. Аналитические показатели ряда динамики и их взаимосвязь.

3. Средние показатели в рядах динамики.

4. Сглаживание рядов динамики. Скользящие средние. Экспоненциальное сглаживание.

5. Вычисление тренда с помощью метода аналитического выравнивания (метод наименьших квадратов).

6. Прогнозирование в бизнесе.

7. Компоненты классической мультипликативной модели рядов динамики.

8. Изучение сезонных изменений.

28.Понятие о статистических рядах динамики. Виды рядов динамики.

Все явления изучаются в развитии. Статистика дает характеристику изменения статистических показателей во времени.

Ряд данных, взятых в определенные периоды времени и представленных в табличной форме называется ряд динамики (временной ряд), т.е. это статистические данные, отображающие развитие изучаемого явления во времени.

Например, ежедневные котировки акций на бирже, образуют ряд динамики. Другим примером ряда динамики являются ежемесячные значения цен потребительской корзины; ежеквартальные значения ВВП; ежегодные доходы от продаж какой-нибудь компании.

В каждом ряду динамики есть два основных элемента:

- показатель времени t,

- соответствующие ему уровни развития изучаемого явления y.

В качестве показателей времени в РД могут быть:

- даты (моменты времени);

- отдельные периоды (сутки, месяцы, кварталы, годы).

Уровни РД отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. Уровни РД могут относиться к определенным датам (моментам) времени, или к отдельным периодам.

В связи с этим РД делятся на:

Моментные – отображают состояние изучаемых явлений на определенные даты (моменты) времени.

Особенность моментного РД – в его уровни могут входить один и те же единицы изучаемой совокупности. Поэтому при суммировании уровней моментного РД может возникнуть повторный счет.

Интервальные - отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Особенность интервального РД – каждый его уровень складывается их данных за более короткие интервалы (субпериоды) времени. Поэтому можно получать РД более укрупненных периодов (свойство суммирования уровней).

29.Аналитические показатели ряда динамики и их взаимосвязь.

В основе расчета показателей ряда динамики лежит сравнение его уровней. Показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же базисным уровнем (полученные показатели называются базисными).

При переменной базе сравнения каждый последующий уровень ряда сравнивается с предыдущим (полученные показатели называются цепными).

Исчисляются следующие аналитические показатели ряда динамики:

1. Абсолютный прирост определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.

Базисный абсолютный прирост ∆y_бi

∆y_бi= y_i- y_бi (1)

цепной абсолютный прирост ∆y_цi

∆y_цi = y_i- y_i-1 (2)

y_i - сравниваемый уровень,

y_бi - уровень, принятый за постоянную базу сравнения.

Абсолютный прирост может иметь и отрицательный знак.

Свойство: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики:

∆y_бn=Σ∆y_цi (3)

2. Темп роста характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах (%).

Базисный темп роста Tр_бi определяется делением сравниваемого значения на уровень, принятый за постоянную базу сравнения:

Tр_бi = y_i / y_бi. (4)

Цепной темп роста Tp_цi определяется делением сравниваемого уровня на предыдущий:

Tр_цi = y_i / y_i-1 (5)

Свойство: произведение последовательных цепных темпов роста равно базисному темпу роста, а частое от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

3. Темпы прироста характеризуют абсолютный прирост в относительных величинах. Они показывают на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Базисный темп прироста Tп_бi определяется как

Tп_бi = ∆y_бi / y_бi. (6)

Цепной темп Tп_цi определяется как

Tп_цi = ∆y_цi / y_i-1 (7)

Взаимосвязь между показателями темпа прироста и темпа роста:

Tп_i (%)=Tp_i (%)-100 при расчете в процентах (8)

Tп_i=Tp_i -1 при расчете в коэффициентах. (9)

С использованием приведенных формул одни показатели м.б. определены по другим.

4. Абсолютное значение одного % прироста (снижения) А_i % -

это отношение абсолютного прироста ∆y_i за определенный период (обычно за год) к темпу прироста Tп_i за этот же период, выраженному в процентах. Этот показатель раскрывает, какая абсолютная величина скрывается за относительной – одним процентом прироста

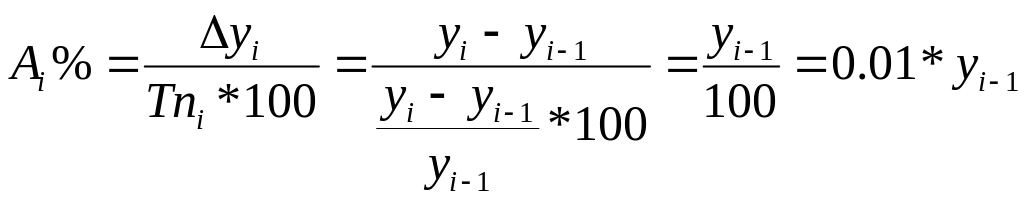(10)

Количественное значение одного % прироста равно одной сотой части уровня, предшествующего анализируемому. Выражается абсолютное значение одного процента прироста (снижения) в единицах измерения уровней анализируемого РД.

5. Темп наращивания Тн_i определяет наращивание во времени исследуемой величины.

Tн_i = ∆y_цi / y_бi., (11)

т.е. определяется делением цепных абсолютных приростов ∆y_цi на уровень, принятый за постоянную базу сравнения y_бi

(12) Эта формула удобна для практического использования.