9. Квадратичные формы в комплексном лп.
 -
полуторалинейная форма.
-
полуторалинейная форма.
 ;
;
 - базис в
- базис в .
.
 –матрица
полуторалинейной формы:
–матрица
полуторалинейной формы: .
.
Определение
9.1
Полуторалинейную форму называют
эрмитовой,
если:
 .
.
Теорема
9.1
Полуторалинейная форма эрмитова ⟺
 .
.
■
«⟹» .
.
«⟸»
Можно представить (упражнение):
 ,
,
 =
=
=
 .
■
.
■
Теорема
9.2
Полуторалинейная форма эрмитова ⟺
 в произвольном базисе эрмитова, т.е.
в произвольном базисе эрмитова, т.е. .
.
■
«⟹» .
.
«⟸» - эрмитова:
- эрмитова: ⟺
⟺ ;
;
 .
■
.
■
Определение
9.2
 - эрмитова полуторалинейная форма в
комплексном ЛП
- эрмитова полуторалинейная форма в
комплексном ЛП .Эрмитовой
квадратичной формой
(эрмитовой формой) называется отображение
.Эрмитовой
квадратичной формой
(эрмитовой формой) называется отображение

 называется
полярной
полуторалинейной формой к эрмитовой
форме
называется
полярной
полуторалинейной формой к эрмитовой
форме
 .
.
Эрмитова
квадратичная форма обладает всеми
свойствами
обычных квадратичных форм.
1)
Полуторалинейная форма, полярная к
эрмитовой форме, определена однозначно.

=
 ,
,
 =
=
=
 =
= .
.
Следовательно,
 ,
,
 .
.
2)
Матрица эрмитовой формы в любом базисе
эрмитова:
 ⟹
⟹
a)
 ,
,
b)
 ,
,
c)
 - в каноническом базисе.
- в каноническом базисе.
3)
Общий вид эрмитовой квадратичной формы:
 .
.
4)
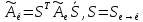
5)
Канонический вид эрмитовой квадратичной
формы:
 .
.
6)
Метод Лагранжа применим и для эрмитовой
квадратичной формы. Изменение алгоритма
состоит в том, что на любом шаге выделяется
полный квадрат модуля:
 .
.
7)
Формулы Якоби остаются в силе.
8)
 принимает вещественные значения.
Следовательно, выполняются закон
инерции, критерий Сильвестра.
принимает вещественные значения.
Следовательно, выполняются закон
инерции, критерий Сильвестра.
2.
14


 -
полуторалинейная форма.
-
полуторалинейная форма. ;
;
 - базис в
- базис в .
. –матрица
полуторалинейной формы:
–матрица
полуторалинейной формы: .
. .
. .
. .
. ,
, =
=
 .
■
.
■ в произвольном базисе эрмитова, т.е.
в произвольном базисе эрмитова, т.е. .
. .
. - эрмитова:
- эрмитова: ⟺
⟺ ;
; .
■
.
■ - эрмитова полуторалинейная форма в
комплексном ЛП
- эрмитова полуторалинейная форма в
комплексном ЛП .Эрмитовой
квадратичной формой
(эрмитовой формой) называется отображение
.Эрмитовой
квадратичной формой
(эрмитовой формой) называется отображение

 называется
полярной
полуторалинейной формой к эрмитовой
форме
называется
полярной
полуторалинейной формой к эрмитовой
форме
 .
.
 ,
, =
= =
= .
. ,
, .
. ⟹
⟹ ,
, ,
, - в каноническом базисе.
- в каноническом базисе. .
.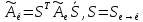
 .
. .
. принимает вещественные значения.
Следовательно, выполняются закон
инерции, критерий Сильвестра.
принимает вещественные значения.
Следовательно, выполняются закон
инерции, критерий Сильвестра.