
- •Раздел 2. Линейные, билинейные и квадратичные формы.
- •1. Линейные формы, сопряженное пространство и его линейность.
- •2. Билинейные (полуторалинейные) формы в линейном пространстве.
- •3. Симметричные и кососимметричные билинейные формы и их матрицы.
- •4. Квадратичные формы в лп.
- •5. Приведение квадратичной формы к каноническому базису методом Лагранжа.
- •6. Приведение квадратичной формы к каноническому виду методом Якоби.
- •7. Закон инерции квадратичных форм.
- •8. Классификация квадратичных форм в вещественном пространстве. Критерий Сильвестра.
- •9. Квадратичные формы в комплексном лп.
6. Приведение квадратичной формы к каноническому виду методом Якоби.
Пусть
в
 задана квадратичная форма
задана квадратичная форма ,
, - матрица квадратичной формы в базисе
- матрица квадратичной формы в базисе .
.
Главные
миноры матрицы
 :
:
 .
.
Теорема
6.1 (Якоби)
Пусть в базисе
 и все главные миноры
и все главные миноры матрицы
матрицы отличны от нуля. Тогда существует базис
отличны от нуля. Тогда существует базис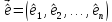 ,
в котором квадратичная форма
,
в котором квадратичная форма приводится к каноническому виду:
приводится к каноническому виду:
 где
где
 - координаты вектора
- координаты вектора в базисе
в базисе .
.
■
Будем
искать
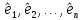 в виде:
в виде:
 ,
,
 ,
,
 , (6.1)
, (6.1)
…
 .
.
Или
 . (6.2)
. (6.2)
Коэффициенты
 ищем из условия:
ищем из условия:
 . (6.3)
. (6.3)
Покажем,
что в базисе
 имеет
имеет диагональный вид. Рассмотрим
диагональный вид. Рассмотрим ;
;
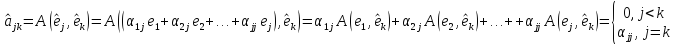 .
.
В
силу симметрии матрицы квадратичной
формы
 .
Следовательно, матрица
.
Следовательно, матрица имеет диагональный вид. При этом:
имеет диагональный вид. При этом: .
Докажем, что
.
Докажем, что определяются однозначно и
определяются однозначно и .
.
Составим
систему уравнений, подставив
 в
в (6.3):
(6.3):

 . (6.4)
. (6.4)
Распишем
(6.4)
 :
:
 ,
,
 ,
,
… (6.5)
 ,
,
Систему (6.5) перепишем в матричной форме:
 ,
(6.6)
,
(6.6)
Определитель
системы (6.5) ((6.6)):
 ,
следовательно, по правилу Крамера
существует единственное решение
,
следовательно, по правилу Крамера
существует единственное решение неоднородной СЛАУ. Так, для
неоднородной СЛАУ. Так, для .
.
Покажем,
что
 образует базис. Действительно, определитель
матрицы перехода имеет вид:
образует базис. Действительно, определитель
матрицы перехода имеет вид:
 .
.
Следовательно,
преобразование невырожденное,
следовательно,
 образуют базис. ■
образуют базис. ■
7. Закон инерции квадратичных форм.
Пусть
в вещественном ЛП
 дана квадратичная форма
дана квадратичная форма ранга
ранга .
.
Из теоремы Лагранжа следует, что квадратичную форму можно привести к виду:
 .
.
Рассмотрим невырожденное преобразование:
 .
.
Следовательно, квадратичная форма примет вид
 ,
(7.1)
,
(7.1)
где
 принимают значения
принимают значения .
.
Определение 7.1 Выражение (7.1) называется нормальным видом квадратичной формы.
Теорема 7.1 (закон инерции вещественных квадратичных форм).
Число положительных коэффициентов в представлении (7.1), называемых положительным индексом инерции, число отрицательных коэффициентов, называемых отрицательным индексом инерции, и число нулевых коэффициентов, называемых дефектом квадратичной формы, являются инвариантами квадратичной формы, т.е. не зависят от базиса, в котором данная квадратичная форма принимает нормальный вид.
■ Пусть существует два базиса, в которых имеет нормальный вид:
 ,
,
 .
.
Надо
доказать, что
 .
.
Пусть
 и
и .
Рассмотрим
.
Рассмотрим - линейную оболочку
- линейную оболочку ,
, - линейную оболочку
- линейную оболочку .
. .
.

 .
.
Следовательно,
существует ненулевой
вектор
 ,
следовательно,
,
следовательно, можно разложить по векторам
можно разложить по векторам и
и :
:
 ,
,
 ,
,
Т.к.
 ,⟹
,⟹
 ,
,
⟹
противоречие,
предположение
 - неверно. Аналогично доказываются
случаи
- неверно. Аналогично доказываются
случаи .
■
.
■
8. Классификация квадратичных форм в вещественном пространстве. Критерий Сильвестра.
Определение
8.1
Вещественная квадратичная форма
 ,
определенная в вещественном ЛП
,
определенная в вещественном ЛП ,
называется:
,
называется:
1)
положительно
определенной,
если
 ;
;
2)
отрицательно
определенной,
если
 ;
;
3)
знакопеременной,
если
 ;
;
4)
квазиположительно определенной, если
 ;
;
5)
квазиотрицательно определенной, если
 .
.
Положительно (отрицательно) определенные квадратичные формы называются знакоопределенными (знакопостоянными); квазиположительно (квазиотрицательно) определенные – называются квазиопределенными.
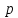 -
положительный индекс инерции;
-
положительный индекс инерции;
 - отрицательный индекс инерции.
- отрицательный индекс инерции.
Теорема 8.1 Вещественная квадратичная форма является:
1)
положительно определенной ⟺
 ;
;
2)
отрицательно определенной ⟺
 ;
;
3)
знакопеременной ⟺
 ;
;
4)
квазиположительно определенной ⟺
 ;
;
5)
квазиотрицательно определенной ⟺
 .
.
■ Докажем случай 1).
«⟹»
Пусть
 - положительно определена и
- положительно определена и ,
следовательно, нормальный вид квадратичной
формы:
,
следовательно, нормальный вид квадратичной
формы:
 ,
,
Рассмотрим
 с координатами:
с координатами: ⟹
⟹
 ⟹противоречие.
⟹противоречие.
«⟸»
Пусть
 ⟹
нормальный вид:
⟹
нормальный вид:
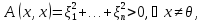 ⟹
⟹
 положительно определена.
положительно определена.
Аналогично 2) – 5). ■
Теорема 8.2 (Критерий Сильвестра)
Пусть
 задана в вещественном ЛП
задана в вещественном ЛП ,
, - главные миноры матрицы
- главные миноры матрицы .
Тогда:
.
Тогда:
1)
 - положительно определена⟺
- положительно определена⟺
 ;
;
2)
 - отрицательно определена⟺
- отрицательно определена⟺
 ,
т.е.
,
т.е. .
.
■ Докажем первый случай. 1)
«⟹» - положительно определена. Докажем, что
- положительно определена. Докажем, что .
От противного. Пусть
.
От противного. Пусть .
Рассмотрим однородную СЛАУ:
.
Рассмотрим однородную СЛАУ:
 ,
,

 ,
,
следовательно,
существует нетривиальное решение
 :
:
 для
для
 . (8.1)
. (8.1)
Умножим
(8.1) на
 и просуммируем:
и просуммируем:
 ,
,
 ,
где
,
где
 ,
,
следовательно,
противоречит тому, что
 - положительно определенная квадратичная
форма,⟹,
- положительно определенная квадратичная
форма,⟹,
 ,⟹,
приведем
,⟹,
приведем к каноническому виду методом Якоби:
к каноническому виду методом Якоби:
 . (8.2)
. (8.2)
В
(8.2) возьмем в качестве

 .
.
«⟸»
Т.к.
 ,то
из разложения Якоби следует, что
,то
из разложения Якоби следует, что
 .
.
2)
Пусть
 - отрицательно определена⟺
- отрицательно определена⟺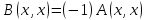 - положительно определена ⟹
- положительно определена ⟹
 ,
,
⟹ -
главные миноры матрицы
-
главные миноры матрицы
 ,
тогда
,
тогда .
Из условия положительной определенности
квадратичной формы
.
Из условия положительной определенности
квадратичной формы следует, что
следует, что .
■
.
■
