Раздел 2. Линейные, билинейные и квадратичные формы.

1. Линейные формы, сопряженное пространство и его линейность.

- ЛП над .

Определение 1.1 Линейный операторназываетсялинейной формой или линейным функционалом.

- вещественная линейная форма,

- комплексная линейная форма.

Примеры: 1) .

2) .

- линейное пространство линейных форм.

Определение 1.2 Пространство - называетсясопряженным к пространству .

Пусть - базис в. Линейная форма однозначно определена числами:- которые называютсякоэффициентами формы в базисе . (Матрица линейного оператора)

Тогда .

Определение 1.3 Представление называетсяобщим видом линейной формы в базисе .

Теорема 1.1 Изменение коэффициентов линейной формы при изменении базиса. , тогда.

∎

⟹ . ∎

Замечание. Коэффициенты линейной формы преобразуются как элементы базиса.

Теорема 1.2 .

∎ . ∎

Следствие. Всякое конечномерное ЛП изоморфно своему сопряженному.

2. Билинейные (полуторалинейные) формы в линейном пространстве.

Пусть - ЛП над.

Определение 2.1 Оператор называетсябилинейной формой, если:

1) ,

2) .

Определение 2.1 Оператор называетсяполуторалинейной формой, если

1) ,

2) .

Примеры: 1) .

2) .

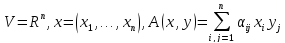3) .

Определение 2.2 .

.

Определение 2.3 Пусть - базис в(над)

- называется общим видом билинейной формы в базисе .

Матрица - называетсяматрицей билинейной формы в базисе .

.

Определение 2.3 Пусть - базис в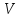(над)

- называется общим видом полуторалинейной формы в базисе .

Матрица - называетсяматрицей полуторалинейной формы в базисе .

Теорема 2.1 Преобразование матрицы билинейной (полуторалинейной) формы при замене базиса.

Пусть - ЛП над.. Тогда.

∎

.

. ∎

Следствие. .

Определение 2.4 Рангом билинейной (полуторалинейной) формы называется ранг ее матрицы в произвольном базисе.

Обозначение: .

Билинейная (полуторалинейная) форма называется вырожденной, если иневырожденной, если .

Теорема 2.2 Пусть ЛП над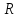,- базис в. Для любого набора чиселсуществует и притом единственная билинейная формав, для которой.

∎ Пусть - базис в- заданные числа. Зададим отображение:- оно является билинейной формой в силу линейности координат, причем.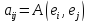

Покажем, что любая билинейная форма , для которойсовпадает с.

. ∎

Теорема 2.3 Существует взаимооднозначное соответствие между множеством всех билинейных форм в - мерном вещественном ЛПи множеством вещественных матриц

∎ Пусть - базис в. Любой билинейной форме поставим в соответствие- матрицу билинейной формы в базисе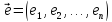. Это отображение сюръективно (Т2.2) и инъективно (различные билинейные формы имеют различные матрицы).∎

3. Симметричные и кососимметричные билинейные формы и их матрицы.

Определение 3.1 Билинейная форма называется симметричной, если и кососимметричной, если.

Теорема 3.1 Любую билинейную форму можно единственным образом представить в виде суммы симметричной и кососимметричной билинейной формы.

∎ .

;

.

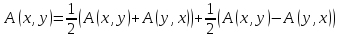Пусть существует другое представление: ⟹

⟹⟹симметричная форма = кососимметричная форма.

Билинейная форма, которая одновременно является симметричной и кососимметричной – это нулевая билинейная форма. ⟹ единственность.∎

Теорема 3.2 Билинейная форма симметрична (кососимметрична) ⟺ ее матрица в произвольном базисе симметрична (кососимметрична).

∎ «⟹» непосредственная проверка:

⟹симметрична;

⟹кососимметрична.

«⟸» - базис в

- симметричная матрица: ⟹ ;

- кососимметричная матрица: ⟹ . ∎