Раздел 4. Линейные операторы в евклидовых (унитарных) пространствах.

1. Сопряженный оператор и его свойства. Матрица сопряженного оператора.

Определение 1.1 Оператор , действующий в унитарном пространстве, называетсясопряженным к линейному оператору , если.

Пример. - фиксирован.

.

Теорема 1.1 Для любого линейного оператора существует и притом единственный сопряженный оператор, при этом он так же линеен, т.е..

∎ Обозначим - полуторалинейная форма в, следовательно, существует единственный линейный оператор, который обозначим.∎

Лемма 1.2 Если и, то.

∎

. ■

Теорема 1.3 Свойства сопряженных операторов:

1) ;

2) ;

3) ;

4) ;

5) ;

6)

выполнены для любых операторов, для которых определены указанные операции.

∎ .

1) .

2)

.

3)

.

4)

.

5) .

6) .∎

Теорема 1.4 (Матрица сопряженного оператора в ОНБ)

Пусть - ОНБ в . Тогда, т.е..

∎ .

,

, ⟹ .∎

Определение 1.2 Матрица , удовлетворяющая условию, называетсясопряженной по отношению к .

Замечание. В произвольном базисе .

⟹

.

Следствия. 1) ;.

2)

Если - собственные значенияалгебраической кратности, то- собственные значения оператораалгебраической кратности.

Теорема 1.5 Пусть - ОНБ в. Тогда- оператор, сопряженный ктогда и только тогда, когда.

∎ «⟹» - оператор, сопряженный к, следовательно, в ОНБ

«⟸»- матрица, сопряженная к:.

Поставим матрицам в соответствие операторы: .

.

.∎

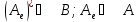Теорема 1.6 (Ядра и образы операторов и)

Для .

∎

С другой стороны: .

Второе аналогично. ∎

Теорема 1.7 Если подпространство инвариантно относительно, то его ортогональное дополнение- относительно:

∎. ∎

2. Нормальный оператор. Нормальная матрица. Свойства нормального оператора. Матрица нормального оператора в онб.

Определение 2.1 Оператор называетсянормальным, если . Матрицаназываетсянормальной, если .

Теорема 2.1 (Свойства нормальных операторов) Пусть – нормальный оператор, тогда

1) ;

2) ;

3) Если - собственный вектор линейного оператора, отвечающий собственному значению, то- собственный вектор, отвечающий собственному значению.

4) Собственные векторы нормального оператора, отвечающие различным собственным значениям, попарно ортогональны.

5) - собственный вектор, то, где- линейная оболочка,- ортогональное дополнение к. Кроме тогои– инвариантные подпространства относительно.

∎ 1) .

2) ⟸ 1).

3) .

a) Покажем, что, если - нормальный, то- нормальный, т.к.

.

b) - собственный вектор линейного операторат.к.- нормальный оператор (свойство 2):

⟹

⟹- собственный вектор , отвечающий собственному значению.

Следствие 1. Если - нормальный оператор, то, т.к. нетривиальные векторы являются собственными векторами, отвечающие собственному значению.

Следствие 2. Если - нормальный оператор, то.

4) Пусть .

⟹

.

5) ,- собственный вектор, отвечающий собственному значению.- линейное подпространство. По теореме о разложении унитарного пространства в прямую сумму:

.

Докажем инвариантность относительно и.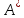

.

.

;

. ∎

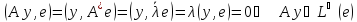Теорема 2.2 Оператор нормален⟺ в ОНБ - нормальная матрица.

∎ –ОНБ в .

- нормальная матрица ⟺ ⟺ (по теореме 1.5) ⟺ ⟺ – нормальный оператор.∎