10. Жорданов базис и жорданова нормальная форма оператора.

Определение 10.1 Жордановой матрицей (или матрицей, имеющей жорданову нормальную форму) называется квазидиагональная матрица с клетками Жордана на главной диагонали. Жордановым базисом для называется базис пространства, в котором матрица оператораимеет жорданову нормальную форму.

Канонический базис корневого подпространства является жордановым для оператора, а– его жордановой матрицей.

Пример. Если - нильпотентный оператор (⟺ все )⟹ существует одно корневое подпространство ⟹ можно найти жорданов базис.

Решим задачу в общем виде.

Теорема 10.1 Пусть в комплексном пространстве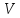, его характеристический многочлен имеет вид: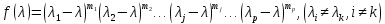. Тогда в ЛПсуществует базис, в котором матрица оператораимеет жорданову нормальную форму:

, где имеют вид- матрицы операторав каноническом базисе.

∎ Согласно Т8.1 (о расщеплении линейного оператора): .

В качестве исходного базиса возьмем совокупность канонических базисов корневых подпространств. Согласно Т1.2 матрица имеет вид, где- матрица оператора.∎

Замечание 1. Жорданова форма матрицы линейного оператора определена однозначно с точностью до порядка клеток Жордана.

Замечание 2. Для операторов простой структуры, и только для них, жорданова форма совпадает с диагональной: .

Приведение матрицы к жордановой форме.

Т.10.1 ⟺ любая квадратичная комплексная матрица эквивалентна матрице, имеющей жорданову форму.

Определение 10.2 Жорданова матрица, эквивалентная матрице , называетсяжордановой нормальной формой матрицы .

Теорема 10.2 Две матрицы эквивалентны⟺ их жордановы формы совпадают.

Привести к жордановой нормальной форме значит найти невырожденную матрицу и жорданову формутакие, что, где- матрица перехода от исходного базиса к жорданову.

11. Многочлен от линейного оператора. Теорема Гамильтона – Кэли.

Пусть - ЛП над.

Рассмотрим .

Определение 11.1 Линейный оператор называетсямногочленом от оператора илиоператорным многочленом.

Теорема 11.1 Пусть - операторные многочлены, тогда:

1. (в частности: )

2. - подпространства, инвариантные относительно .

∎ 1) .

2)

. ∎

Теорема 11.2 - некоторый многочлен степени,- собственное значение,- собственный вектор, отвечающий собственному значению. Тогда- собственный вектороператора , отвечающий собственному значению, причем, если;, если.

∎ ;

.

Если .

Если .∎

Замечание (матричная формулировка операторных свойств).

Определение 11.1 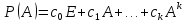- многочлен от матрицы

Теорема 11.1 .

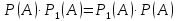Теорема 11.3 (теорема Гамильтона – Кэли) Линейный оператор , действующий в комплексном или вещественном пространстве, является корнем своего характеристического многочлена.

∎ Дано: - характеристический многочлен;

- оператор;

.

Надо доказать, что - нулевой оператор.

1) Докажем для комплексного пространства ,

⟹ где ,

⟹.

Произведения в операторе перестановочны (Т11.1), а⟹ .

2) - вещественное пространство,- любой базис (какой-нибудь) пространства.- матрица оператора.- любое комплексное пространство:- базис. Тогда- матрица некоторого оператораих многочлены совпадают и.∎

Определение 11.2 Многочлен называетсяаннулирующим многочленом для , если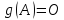. Аналогично для матрицы.

Из теоремы Гамильтона- Кэли следует, что существует аннулирующий многочлен степени .

Определение 11.3 Многочлен наименьшей степени со старшим коэффициентом единица, аннулирующий, называетсяминимальным многочленом для .

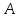Минимальный многочлен определен однозначно: - аннулирующийи имеет строго меньшую степень.

Теорема 11.4 Минимальный многочлен является делителем аннулирующего многочлена.

∎ От противного: , гдеили– минимальный⟹ противоречие .∎

Замечание. С помощью жордановой формы легко вычислить минимальный многочлен. Для ⟹ для – максимальный размер жордановой клетки, отвечающий данному