5. Операторы простой структуры. (Диагонализуемость линейного оператора.) Критерий диагонализуемости линейного оператора.

Определение 5.1 Линейный оператор называетсяоператором простой структуры, если в ЛП существует базис из собственных векторов оператора.

Теорема 5.1 Линейный оператор имеет простую структуру⟺ существует базис, в котором он имеет диагональную матрицу.

∎ Линейный оператор простой структуры ⟺ существует базис из собственных векторов ⟺ , где.∎

Следствие. В -мерном пространстве линейный оператор, имеющийразличных собственных значений, является оператором простой структуры.

Оператор простой структуры называют также диагонализуемым оператором.

Теорема 5.2 Линейный оператор - диагонализуемый⟺ все его собственные подпространства в прямой сумме дают все ЛП , т.е..

∎ «⟹» Пусть - диагонализуемый⟹ существует базис из собственных векторов . Рассмотрим подпространство. С другой стороны, любой изпринадлежит некоторому из⟹ ⟹ (прямая).

«⟸» Из критерия прямой суммы и линейной независимости собственных векторов, отвечающих различным собственным значениям: - базис в- совокупность базисов – базис в.∎

Замечание. Условие может быть заменено условием.

Теорема 5.3 Линейный оператор, действующий в комплексном пространстве, имеет простую структуру ⟺ когда для любого собственного значения геометрическая кратность совпадает с алгебраической кратностью.

∎ Пусть - различные собственные значения.– алгебраическая и геометрическая кратность.

«⟸» Если алгебраическая кратность совпадает с геометрической , то(В- мерном комплексном пространстве существуетсобственных значений, если любой корень считать столько раз, какова его кратность).

«⟹». Но равенствовозможно только при условии.∎

Замечание. (матричная формулировка операторных свойств) Пусть

1) Ненулевой вектор-столбец называетсясобственным вектором матрицы 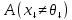, если существует=,-собственное значение матрицы.

2) называетсяматрицей простой структуры (диагонализуемой), если она имеет линейно независимых собственных векторов.

3) Критерий 5.4 (матричная формулировка критерия 5.1) Квадратная матрица является матрицей простой структуры ⟺ она эквивалентна диагональной.

В комплексном пространстве не каждый линейный оператор обладает необходимым для базиса числом линейно независимых собственных векторов.

Пример. Матрица называетсяжордановой клеткой -того порядка.

1) - характеристический многочлен.

2) - алгебраической кратности.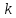

3) собственные векторы, являются нетривиальными решениями ОСЛАУ ⟹ ⟹ имеет один собственный вектор ⟹ не является матрицей простой структуры.

6. Треугольная форма матрицы линейного оператора.

Теорема 6.1 В –мерномкомплексном линейном пространстве для любого линейного операторасуществует системавложенных друг в друга инвариантных подпространств всех размерностей от 1 до, таких , что, где.

∎(по индукции)

- очевидно.

Пусть утверждение верно для ЛП размерности . Докажем для ЛП.

Лемма. Линейный оператор, действующий в мерномкомплексном пространстве, обладает инвариантным подпространством размерности .

Доказательство леммы. Линейный оператор, действующий в ЛП , имеет собственное значениеПусть- собственный вектор, отвечающий собственному значению⟺ ⟹ существует ЛПП , которое содержит. Покажем, чтоинвариантно относительно л.о.Лемма доказана.

Итак, л.о. , действующий вимеет инвариантное подпространстворазмерности.

Индуцированный оператор действует в пространстве размерностьюи, следовательно согласно предположению индукции существует система вложенных подпространств.

Так как действия операторов инасовпадают, тоинвариантны относительно. Следовательно,.∎

Теорема 6.2 Для любого л.о. , действующего вкомплексном ЛП, существует базис, в котором матрица линейного оператора имеет треугольную форму.

∎ Из Т6.1 ⟹ для л.о. существует система. Строим искомый базис:- базис в;- дополнениедо базиса; …дополнениедо…. В силу инвариантностиимеет верхнюю треугольную форму.∎

Замечание. На главной диагонали стоят собственные значения оператора.

Теорема 6.3 Любая квадратная комплексная матрица эквивалентна матрице, имеющей треугольную форму.