Лекции по линейной алгебре / Лекции Б3 раздел 3

Раздел 3. Евклидовы и унитарные пространства.

1. Определение и примеры евклидовых и унитарных пространств. Линейные нормированные пространства.

Определение 1.1 Пусть - вещественное или комплексное ЛП. Отображение ( или) называется скалярным произведением, если

1)

2)

3)

4)

Число называется скалярным произведением; 1) – 4) – аксиомами скалярного произведения.

Вещественное ЛП со скалярным произведением называется евклидовым пространством: ; комплексное ЛП со скалярным произведением называется унитарным пространством: .

Примеры:

1)

2)

3)

Простейшие свойства скалярного произведения:

1) ;

2) ;

3) ;

4) .

■ 3) .

4) «⟸» 3)

«⟹». ■

Теорема 1.1 (неравенство Коши – Буняковского) Для или .

■ Пусть :

.

Т.к. , пусть .

Тогда . ■

Определение 1.2 Линейное комплексное пространство называется линейным нормированным пространством, если для ставится в соответствие вещественное число , называемое нормой указанного элемента, при этом норма удовлетворяет следующим аксиомам:

1) ;

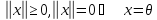2) - однородность нормы;

3) – неравенство треугольника.

Примеры:

1) - длина .

2)

Теорема 1.2 Всякое унитарное пространство является нормированным, если в нем определить норму: .

■1) (аксиома 4),

2) ,

3)

(неравенство Коши Буняковского) . ■

Замечание 1) (неравенство Коши – Буняковского).

2) Введем функцию – расстояние между и :

1) ,

2) ,

3) .

Теорема 1.3 Неравенство: .

■ ;

,

. ■

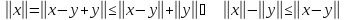Замечание 3) В евклидовом пространстве углом между ненулевыми векторами и называется угол , для которого .

Примеры (неравенства Коши – Буняковского и треугольника)

1)

.

2)

.

2. Общий вид скалярного произведения в унитарном пространстве. Матрица Грама.

Пусть – базис в .

,

.

Обозначим: .

Рассмотрим матрицу .

Определение 2.1 Матрица называется матрицей Грама системы векторов :

.

Запись называется общим видом скалярного произведения в унитарном пространстве.

Замечание1) Т.к. – эрмитова матрица.

2) - евклидово пространство: - симметричная матрица и - общий вид скалярного произведения в евклидовом пространстве.

Теорема 2.1 Пусть и базисы в . Тогда .

■ . ■

3. Ортонормированная система. Ортонормированный базис (ОНБ).

Определение 3.1 Элементы называются ортогональными , если их скалярное произведение равно нулю: .

Замечание 1. Нулевой элемент , и только нулевой, ортогонален любому вектору пространства.

Определение 3.2 Система векторов унитарного пространства называется ортонормированной (ОНС), если (символ Кронекера).

Теорема 3.1 Ортогональная система ненулевых векторов - линейно независима.

∎ Пусть ортогональная система. Достаточно доказать, что равенство достигается только при . Умножим скалярно на , т.к. .∎

Следствие 1. Ортонормированная система векторов линейно независима.

Следствие 2. В - мерном пространстве любая ОНС из векторов образует базис.

Теорема 3.2 В евклидовом (унитарном) пространстве координаты вектора в базисе вычисляются по правилу тогда и только тогда, когда - ортонормированный базис.

∎ «⟹» Пусть . Тогда - тоже вычисляются по этому же правилу. Следовательно, .

«⟸» Пусть - ОНБ, следовательно, из линейности скалярного произведения ⟹ .∎

Теорема 3.3 В унитарном пространстве скалярное произведение векторов и вычисляется по правилу тогда и только тогда, когда - ОНБ.

∎ «⟹» .

«⟸» В силу линейности скалярного произведения. ∎

Замечание 2. В евклидовом пространстве .

4. Существование ОНБ.

Теорема 4.1 (Шмидта об ортогонализации) Пусть в унитарном пространстве задан произвольный базис . Тогда в существует ОНБ , который можно построить следующим образом: , где .

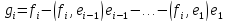∎ Построение ОНБ методом математической индукции.

, т.к. система линейно независима.

Пусть в унитарном пространстве , размерности , существует ОНБ и , .

Докажем, что в унитарном пространстве размерности существует ОНБ. Пусть - произвольный базис . – линейная оболочка - есть унитарное –мерное пространство. Следовательно, по предположению индукции в нем существует ОНБ , удовлетворяющий условиям теоремы. Рассмотрим вектор - линейная комбинация 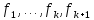. Т.к. линейно независимы, ⟹, . Числа подберем так, чтобы . Умножим на :

Положим . Следовательно, образуют базис в .∎

Следствие. Во всяком –мерном пространстве существует ОНБ.

5. Ортогональное дополнение.

Определение 5.1 Пусть – линейное подпространство унитарного (евклидова) пространства: . Вектор называется ортогональным к подпространству , если он ортогонален :

.

.

Определение 5.2 Подпространства и называются ортогональными .

Определение 5.3 Совокупность всех векторов , ортогональных подпространству , называется ортогональным дополнением к до пространства и обозначается :

.

Теорема 5.1 Ортогональное дополнение является линейным подпространством.

∎ . ∎

Теорема 5.2 .

∎ Пусть . ∎

Теорема 5.3 Унитарное пространство есть прямая сумма любого своего подпространства и его ортогонального дополнения ,т.е. .

∎ Пусть Если ⟹ - тривиальное подпространство. – ОНБ в . Дополним его до базиса (по теореме о неполном базисе): 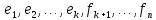. Ортонормируем систем (теорема Шмидта) ⟹ получим ОНБ в . Покажем, что .

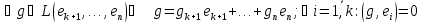, т.к. – ОНБ в ⟹ .

Обратно: , где .

Т.к. . ∎

6. Представление линейной формы в унитарном (евклидовом) пространстве.

Теорема 6.1 - унитарное пространство. Для любой линейной формы в унитарном пространстве существует, и притом единственный, вектор такой, что .

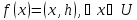∎ Пусть - ОНБ в , - коэффициенты линейной формы в базисе , т.е. .

.

Рассмотрим , тогда

.

Следовательно, - удовлетворяет условию .

Докажем единственность.

Пусть . ∎

- пространство, сопряженное к .

В определим функционалы . Их достаточно определить на базисных векторах:

.

Покажем, что образуют базис в .

∎1) ⟹ их .

2) Докажем линейную независимость.

- нулевой функционал: .

Положим ⟹ линейно независимы ⟹ образуют базис.∎

Определение 6.1 называется биортогональным базисом к базису .

7. Представление полуторалинейной (билинейной) формы в унитарном (евклидовом) пространстве с помощью линейного оператора.

- унитарное пространство. - пространство линейных операторов из в .

Теорема 7.1 Для любой полуторалинейной (билинейной) формы в унитарном (евклидовом) пространстве существует единственный линейный оператор такой, что , причем матрица полуторалинейной формы (билинейной формы ) и матрица оператора в произвольном ОНБ связаны соотношением:

∎ Доказательство проведем для полуторалинейной формы.

1) Возьмем и зафиксируем . Тогда - линейная форма аргумента . Следовательно, . Таким образом построили отображение: . Следовательно, задали оператор .

Покажем, что построенный оператор линеен. .

.

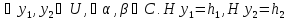2) Докажем единственность. Пусть .

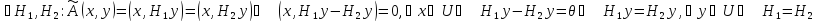3) . ∎

3.12