Фотоэффект. Эффект Комптона

1. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта λ_кр = 307 нм и максимальная кинетическая энергия фотоэлектрона равна 1 эВ?

2. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов U₁ = 3,7 В. Если платиновую пластинку заменить другой пластинкой, то задерживающая разность потенциалов придется увеличить до 6 В. Определить работу выхода электронов с поверхности этой пластинки (Работа выхода фотоэлектрона с поверхности платины 6,3 эВ).

3. На цинковую пластинку падает монохроматический свет с длиной волны λ = 220 нм. Определить максимальную скорость фотоэлектронов (работа выхода фотоэлектронов с поверхности цинка 4 эВ).

4. Определить работу выхода электрона из натрия, если красная граница фотоэффекта λ_кр = 500 нм.

5. На поверхность лития падает монохроматический свет (λ = 310 нм). Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов не менее 1,7 В. Определить работу выхода А.

6. Определить максимальное изменение длины волны при комптоновском рассеянии: а) на свободных электронах, б) на свободных протонах (масса покоя электрона 9,1·10^-31 кг, масса покоя протона 1,67·10^-27 кг).

7. Фотон с энергией ε = 0,4 МэВ рассеялся под углом θ = 90° на свободном электроне. Определить энергию ε^/ рассеянного фотона и кинетическую энергию электрона отдачи.

8. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян на угол θ = 180°.

9. Фотон с энергией ε = 0,25 МэВ рассеялся на свободном электроне. Энергия ε^/ рассеянного фотона равна 0,2 МэВ. Определить угол рассеяния θ.

10. Рентгеновское излучение длиной волны λ = 55,8 пм рассеивается плиткой графита (комптон-эффект). Определить длину волны λ^/ света, рассеянного под углом θ = 60° к направлению падающего пучка света.

12. Определить угол рассеяния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии Δλ = 3,62 пм.

Гипотеза де Бройля. Соотношения неопределенностей Гейзенберга

1. Кинетическая энергия протона в 4 раза меньше его энергии покоя. Вычислить длину волны де Бройля для такого протона. (Энергия покоя протона W_оp = 1,5·10^-10 Дж).

2. Определите, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля λ для него была равна 1 пм.

3. Кинетическая энергия электрона Т = 0,6 МэВ. Определите длину волны де Бройля. (Энергия покоя электрона W₀ = 0,511 МэВ).

4. Какой кинетической энергией должен обладать протон, чтобы его длина волны де Бройля равнялась его комптоновской длине волны?

4. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля λ = 2,02 пм. Найти массу m частицы, если ее заряд численно равен заряду электрона.

5. Электрон прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля для случаев: U₁ = 51 В, U₂ = 510 кВ.

6. Кинетическая энергия электрона в атоме водорода порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.

7. Среднее время жизни атома в возбужденном состоянии равно 12 нс. Вычислить минимальную неопределенность Δλ длины волны λ = 12 мкм излучения при переходе атома в основное состояние (Формулу энергии излучаемого фотона продифференцировать и перейти к Δ, использовать соотношение неопределенностей энергии и времени).

4. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10^-8 с, определите отношение естественной ширины ΔЕ энергетического уровня, на который был возбужден электрон, к энергии Е, излученной атомом.

Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга

Если протон и дейтрон прошли одинаковую ускоряющую разность потенциалов, то отношение их длин волн де Бройля равно …

Решение:

Дейтрон – ядро тяжелого изотопа водорода (дейтерия). Длина волны де Бройля

определяется по формуле: где p – импульс частицы. Импульс частицы можно выразить через ее кинетическую энергию По теореме о кинетической энергии, согласно которой работа сил электрического поля идет на приращение кинетической энергии, Отсюда можно найти Е_k, полагая, что первоначально частица покоилась: Окончательное выражение для длины волны де Бройля через ускоряющую разность потенциалов имеет вид: 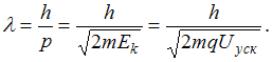Учитывая, что и отношение длин волн де Бройля протона и дейтрона равно: