8. Сызықтық дифференциалдық жүйе үшін Остроградский-лиувилль формуласы.

Остроградский -Лиувилль формуласын келтірейік.

Алдымен, -ші ретті анықтауыштың туындысы қалай ашылатынын көрсетейік.

-ші ретті анықтауыштың туындысы сол анықтауыштың әр бағанасы (немесе әр жатық жолы) кезекпен туындыларымен ауыстырылған анықтауыштардың қосындысынан тұрады. Осы ереже бойынша вронскианның туындысын ашайық:

(24)

Мұндағы, берілген жүйенің шешімі болғандықтан,

Осы өрнектерді анықтауыштың -нші бағанасына қойсақ, анықтауыштың қасиеттері бойынша, болатын қосындыдан басқа анықтауыштардың бәрі нөлге тең болады, өйткені олардың екі бағанасы өзара пропорционал болады. Сондықтан,

Осыдан

(25)

Мұндағы, - берілген матрицасының ізі деп аталады.

Осы (25) теңдікті Остроградский-Лиувилль формуласы деп атайды. Бұл формуладан мынандай қорытынды шығады: егер аралығының бір нүктесінде вронскиан нөлге тең болса, ол бүкіл аралықта нөлге тең болады, ал аралығының бір нүктесінде нөлге тең болмаса, онда ол бүкіл аралықта нөлге тең болмайды.

9-сурак.Сызықты біртекті емес жүйенің жалпы шешімін табу үшін тұрақтыларды вариациялау әдісі. Төмендегідей біртексіз сызықты теңдеуді қарастырайық:

(1)

Мұнда да коэффициенттер мен бос мүше кейбір аралығында үздіксіз функциялар деп есептелінеді. Осы теңдеудің сәйкес біртектісін қоса қарастырайық:

(2)

Біртексіз теңдеудің жалпы шешімін табу үшін әдетте, тұрақтыларды вариациялау әдісі қолданылады. Бұл әдістің мәнісі – сәйкес біртекті теңдеудің жалпы шешімі белгілі деп, ондағы еркін тұрақтыларды -қа байланысты айнымалы шамалар деп есептелініп, шешім мына түрде ізделінеді:

(3) мұндағы, - біртекті теңдеудің фундаменталь шешімдері. Осындағы функцияларын (3) қосынды (1) теңдеудің шешімі болатындай етіп таңдайды. Бұл функцияларды анықтау үшін теңдеу керек. Ол үшін (3) өрнекті ретке дейін дифференциалдаймыз. Мұнда функцияларының туындыларына қосымша шарт қойылып отырады.

Сонымен,

Осындағы екінші қосындыны нөлге теңейміз:

Қалған бірінші қосындыдан екінші туынды табамыз:

Осындағы екінші қосындыны тағы да нөлге теңейміз:

Осылай қосындыны рет дифференциалдап, туындыларының қосындысын әрдайым нөлге теңеп отырамыз. Сонда

,

ал

Соңғы екінші қосындыны нөлге теңестірмейді. Ол қосынды (1) теңдеудің оң жағындағы функциясына тең деп алынады.

Себебі, (3) өрнекті және оның туындыларын (1) теңдеуге апарып қойсақ, төмендегідей теңдік аламыз:

мұнда .

10)Коэфф-рі тұрақты сыз-қ біртекті жүйені Эйлер әдісімен шешу. Түбірлері әртүрлі болатын жағдай. Алдымен біртекті теңдеуді қарастырайық:

(1)

Мұндағы, - тұрақты нақты сандар.

Бұл теңдеудің шешімін Эйлер ұсынған әдіс бойынша

(2)

түрінде іздейміз. Мұндағы, - белгісіз тұрақты сан. Осы өрнекті (1) теңдеудің сол жағына қойсақ,

(3)

қатынасын аламыз. Мұнда

(3) қатынастан функциясы теңдеудің шешімі болу үшін санының теңдеуінің шешімі болуы керек екенін көреміз, яғни

Соңғы теңдеуді сипаттаушы теңдеу деп, ал оның түбірлерін сипаттаушы сандар деп атайды. Сипаттаушы сандардың түрлеріне байланысты фундаменталь шешімдер жүйесі әртүрлі болады.

1. Сипаттаушы сандардың ішінде комплексты сандар кездессін. Айталық, - сипаттаушы теңдеудің жәй түбірі болсын. Онда оның түйіндесі саны да сол теңдеудің түбірі болады. Бұл жағдайда түбіріне сәйкес шешім

түрінде жазылады. Бұл комплексты функция. Сызықты теңдеудің шешімдерінің қасиеті бойынша оның нақты және жорамал бөліктері өз алдына берілген теңдеудің шешімдері болады. Сондықтан,

(4)

функциялары (1) теңдеудің шешімдері болады және олар өзара сызықты тәуелсіз. Ал түбіріне сәйкес шешім де сол өзара тәуелсіз екі функцияны береді:

(5)

Бұлардың біріншісі, алдыңғымен бірдей; екіншісі, тек таңбасымен өзгеше, яғни (4) және (5) функциялар өзара сызықты тәуелді. Сондықтан, өзара түйіндес комплекс түбір үшін (4) түріндегі екі нақты функция алынады. Осы сияқты, кез келген қос комплексты түбір үшін екі нақты функциялар алынып отырады. Оларға қоса нақты түбірлерге сәйкес қойылатын шешімдерді алсақ, олардың жиыны берілген теңдеудің фундаменталь шешімдер жүйесін құрайды.

2. Сипаттаушы теңдеудің түбірлерінің кейбіреулері еселікті түбірлер болсын.

Айталық, -саны сипаттаушы теңдеудің -еселікті түбірі болсын. Бұл жағдайда

шарттары орындалады.

тепе-теңдігін бойынша рет дифференциалдайық:

Осыдан (11) шартты ескерсек:

болатынын көреміз, яғни

(6)

функцияларының (1) теңдеудің шешімдері болатынын көреміз. Бұл шешімдердің де өзара сызықты тәуелсіз екенін көрсету қиын емес. Мұнда, -саны нақты болса, онда (6) функциялар да нақты функциялар болады. Егер сипаттаушы теңдеудің комплексты түбірі еселікті түбір болса, оның түйіндесі түбірі де еселікті болады. Бұл жағдайда да алдыңғы (6) шешімдер сияқты төмендегідей шешім аламыз:

Осы комплексты функциялардың нақты және жорамал бөліктерін ажыратсақ, онда нақты функциялардың жиынын аламыз:

Түйіндес түбірі жаңа тәуелсіз шешімдер тудырмайды.

11) Коэффиценттері тұрақты сызықтықтық біртекті жүйенің сипаттаушы тең-ң түбірлері әр түрлі комплекс мәнді болғандағы нақты шешімдерін құру.

Коэффициенттері тұрақты біртекті сызықты жүйені қарастырайық:

(1)

Мұнда - тұрақты нақты квадрат матрица.

Сипаттаушы сандары әртүрлі нақты сандар болсын.

Бұл сандарды кезекпен мына қатынасқа қойып, дербес шешім табамыз:

(2)

Олардың сызықты тәуелсіздігін көрсету үшін Вронский анықтауышын құрайық:

Ол сандары әртүрлі болғанда нөлге айналмайды, яғни . Сондықтан, (2) функциялар жиыны берілген теңдеудің фундаменталь шешімдер жүйесін құрайы. Бұл жағдайда жалпы шешім

түрінде жазылады. Мұндағы, - еркін тұрақты сандар.

Түбірлері әртүрлі комплекс мәнді болғандағы нақты шешімін құру. Коэффициенттері тұрақты біртекті сызықты жүйені қарастырайық. (1)

Мұнда - тұрақты нақты квадрат матрица.

Мұнда -белгісіз сан, -нөлдік емес белгісіз тұрақты вектор.

Осы өрнекті (1) жүйеге қойсақ,

түріндегі векторлық алгебралық теңдеу аламыз. Бұл теңдеуді ашып жазсақ,

сызықты теңдеулер жүйесін аламыз. Жүйенің нөлдік емес шешімі бар болуы үшін оның анықтауышы нөлге тең болуы керек:

немесе

Осы теңдеу берілген жүйенің сипаттаушы теңдеуі деп аталады

- сипаттаушы теңдеудің жәй түбірі болсын. Онда оның түйіндесі саны да сол теңдеудің түбірі болады. Бұл жағдайда сәйкес шешім

түрінде жазылады. Соңғы қатынастың нақты және жорамал бөліктерін ажыратайық:

Жүйенің коэффициенттері нақты болғандықтан, комплекс шешімнің нақты және жорамал бөліктері өз алдарына нақты шешімдер болып табылады. Сондықтан,

функциялары берілген жүйенің нақты шешімдері болады. Бұл шешімдер өзара сызықты тәуелсіз.Түйіндес түбірі жаңа тәуелсіз шешімдер тудырмайды. Демек, бір жұп комплексті түбірге өзара тәуелсіз екі нақты шешім сәйкес келеді. Олар өзара сызықты тәуелсіз болғандықтан, фундаменталь шешімдер жүйесіне кіреді. Осы сияқты, барлық түбірлер үшін нақты шешімдерді құрып шығуға болады. Олардың сызықты комбинациясы жүйенің жалпы шешімін береді.

12) . Коэффиценттері тұрақты сызықтықтық біртекті тең-ң сипаттаушы тең-ң еселі нақты түбіріне сәйкес келетін шешімшің түрі.

Коэффициенттері тұрақты біртекті сызықты жүйені аламыз: (1)Мұнда - тұрақты нақты квадрат матрица.Мұнда -белгісіз сан, -нөлдік емес белгісіз тұрақты вектор.Осы өрнекті (1) жүйеге қойсақ,

түріндегі векторлық алгебралық теңдеу аламыз. Бұл теңдеуді ашып жазсақ,

түріндегі сызықты теңдеулер жүйесін аламыз. Жүйенің нөлдік емес шешімі бар болуы үшін оның анықтауышы нөлге тең болуы керек: немесе

Осы теңдеу берілген жүйенің сипаттаушы теңдеуі деп аталады. Оның түбірлері матрицасының меншікті сандары (мәндері), ал әрбір меншікті санға сәйкес векторын матрицасының меншікті векторы деп атайды. Сипаттаушы теңдеудің түбірлерінің кейбіреулері еселікті түбірлер болатын жағдай. Айталық, -саны - еселікті түбір болсын. Бұл түбірге бір немесе бірнеше меншікті векторлар сәйкес келуі мүмкін. Олардың саны жалпы алғанда -дан аспайды. Сондықтан, формула бойынша анықталатын шешімдердің саны -дан кем болуы мүмкін. Осы жетпей жатқан шешімдерді толықтыру үшін төмендегідей әдіс қолданылады.

векторы жүйенің шешімі болсын.

- дифференциалдық оператор енгізу арқылы берілген жүйені координаттары бойынша ашып жазайық:

(2)

Бұл сызықты жүйенің анықтауышы . Ол -операторы бойынша дәрежелі көпмүшелік. Егер -ның орнына -ны қойсақ, ол сипаттаушы көпмүшелікке айналады. Құрылған мына ₍₂₎ қатынасты анықтауышының алгебралық толықтауышы -ға көбейтіп, -индексі бойынша қосындыласақ,

теңдеуін аламыз. Бұл бойынша -ретті дифференциалдық теңдеу. Оның сипаттаушы көпмүшелігі (1) жүйенің сипаттаушы көпмүшелігіне тең. Сондықтан, мына теңдеудің -еселікті түбіріне сәйкес келетін (1) жүйенің шешімінің -інші компоненті мына түрде жазылады:

Мұнда - тұрақты сандар. Сонымен,

3)

Бұл шешімдегі тұрақты сандарының бәрі бірдей еркін бола алмайды, өйткені шешімінің компоненттері (2) қатынас арқылы өзара сызықты байланысқан. Бұл тұрақтылардың ішінде тәуелсіздерінің саны - түбірінің еселігіне тең, яғни -ға тең. Осы еркін тұрақтыларды - деп белгілейік. (3) шешімді (1) жүйеге қойып, алдын ала - ға қысқартып, -ның бірдей дәрежелерінің коэффициенттерін теңестірсек, біртекті теңдеулердің сызықты жүйесін аламыз. Ондағы белгісіз тұрақтыларының саны . Оларды еркін тұрақтылары арқылы өрнектесек, онда (3) шешімді былай жазуға болады:

Мұндағы, - векторларының компоненттері бойынша дәрежелері - ден аспайтын көпмүшеліктер құрайды. Сипаттаушы теңдеудің еселікті түбіріне түріндегі шешім сәйкес қойылды. Осы сияқты кез келген еселікті түбіріне де сәйкес шешім құрып шығуға болады. Олардың жиыны берілген жүйенің фундаменталь шешімдер жүйесі болатынын көрсету үшін вронскианның нүктесінде нөлге айналмайтынын көрсетсе, жеткілікті.

13. Бірінші ретті дербес туындылы дифференциал теңдеулер үшін Коши есебінің қойылуы. І ретті д/т ДТ түрлері. Бірінші ретті дербес туындылы дифференциал теңдеудің жалпы түрі былай жазылады:

(1)

Мұндағы - белгісіз функция, - тәуелсіз айнымалылар. - кейбір облысында екі рет үздіксіз дифференциалданатын функция болсын.

Анықтама. Кейбір облысында анықталған үздіксіз дифференциалданатын функциясы (1) теңдеудің шешімі деп аталады, егер ол төмендегідей шарттарды қанағаттандырса:

1)

2)

Бұл функциясы - кеңістігінде кейбір

бетті анықтайды. Осы бетті берілген теңдеудің интегралдық беті деп атайды.

Бірінші ретті дербес туындылы теңдеулерді интегралдау әдетте жәй дифференциал теңдеулер жүйесін интегралдауға келтіріледі. Сондықтан, мұндай теңдеулер жәй дифференциал теңдеулер бағдарламасына енгізілген.

Біз бұл жерде бірінші ретті дербес туындылы теңдеулердің тек

екі сызықты түрін ғана қарастырамыз.

Біртекті және біртексіз сызықты теңдеулер үшін Коши есебі былай қойылады:

теңдеудің шешімдерінің ішінен оның бір аргументі тұрақталған жағдайда белгілі бір - өлшемді бетке айналатын дербес шешімді анықтау керек, яғни шешімінің болғанда белгілі функциясына тең болатын шешімді табу керек. Мұны қысқаша (20)

түрінде жазады. Мысалы, екі өлшемді дербес туындылы

теңдеуі үшін Коши есебі былай қойылады:

шешімінің болғанда шартын қанағаттандыратын шешімді іздеу. Ол барлық интегралдық беттердің ішінен қисығы арқылы өтетін бетті табу болып есептелінеді. Жалпы жағдайда Коши есебінің шешімін табу қиындық тудырмайды.

Мысалдар.

1. теңдеуінің жалпы шешімін табайық. Сәйкес сипаттаушы симметрия жүйесін құрайық:

Осыдан интегралдарын табамыз. Бұл жағдайда жалпы шешім түрінде жазылады. Дифференциалдау арқылы бұл функцияның шешім болатынына көз жеткізу оңай.

2. теңдеуінің жалпы шешімін құрайық. Сәйкес

жүйесінің екі тәуелсіз интегралдары оңай табылады:

Жалпы шешім айқындалмаған түрде жазылады:

Осы қатынасты екінші аргументі бойынша шешсек,

түріндегі шешім аламыз

14. Бірінші ретті дербес туындылы сызықты біртекті дифференциал теңдеуді интегралдаудың сипаттауыштар әдісі. біртекті сызықты теңдеуді қарастырайық: (2)

Мұндағы, - функциялары кейбір облысында үздіксіз

дифференциалданатын және бәрі бірдей нөлге айналмайтын

функциялар деп есептелінеді. Бұл (2) теңдеуге төмендегідей жәй дифференциал теңдеулердің симметриялық түрі сәйкес қойылады.

(3)

Осы жүйені (2) теңдеудің сипаттаушы жүйесі деп атайды. Оның интегралдық қисықтары (2) теңдеудің сипаттауыштары (характеристикалары) деп аталады. Бұл жүйенің барлық уақытта шешімдері бар және ол жалғыз. Сондықтан, облысының әрбір нүктесі арқылы тек бір ғана сипаттауыш өтеді және олардыңғ тәуелсіздерінің саны - ге тең, себебі, ол - ретті қалыпты жүйеге эквивалент.

Теорема-1. облысында анықталған үздіксіз дифференциалданатын функциясы (2) теңдеудің шешімі болуы үшін оның (3) жүйенің интегралы болуы қажетті және жеткілікті.

Дәлелдеуі. 1) қажеттілігі. Айталық, функциясы (2) теңдеудің шешімі болсын: (4)

Бұл функцияның толық дифференциалы былай жазылады:

(5)

Осындағы әрбір -дің орнына оған пропорционал функциясын қойсақ, төмендегідей қатынас аламыз:

(6)

Мұндағы, - пропорция коэффициенті. Алдыңғы (4) тепе-теңдікті ескерсек, квадрат жақшаның ішіндегі өрнек нөлге тепе-тең болады, яғни

(7)

Ал бұл тепе-теңдік функциясының (3) жүйенің интегралы болатынын білдіреді.

2) жеткіліктілігі. Айталық, функциясы (3) жүйенің интегралы болсын: (8)

Соңғы тепе-теңдік функциясының (2) теңдеудің шешімі екенін көрсетеді.

Теорема-2. Берілген (2) теңдеудің жалпы шешімі

(9)

түрінде анықталады. Мұндағы, - кез келген үздіксіз дифференциалданатын функция, ал - (3) жүйенің тәуелсіз интегралдары.

Дәлелдеуі. Айталық, кейбір функциясы (2) теңдеудің облысындағы кез келген шешімі болсын. Бұл шешім функцияларымен қоса (2) теңдеуді тепе-теңдікке айналдыра 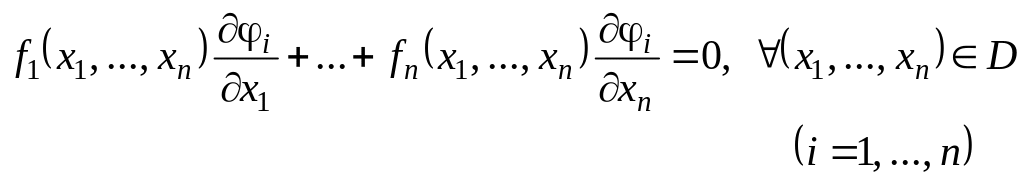(10)

Бұл біртекті сызықты жүйенің нөлдік емес

шешімі бар. Сондықтан, бұл жүйенің анықтауышы нөлге тең. Ол функцияларының якобианына тең. (11)

Соңғы қатынас функцияларының өзара тәуелділігін көрсетеді. Олардың алдыңғы функциялары өзара тәуелсіз функциялар еді. Сондықтан тәуелділікті соңғы функциясы беріп тұр:

(12)

Мұндағы, - кез келген шешім боғандықтан, (12) қатынас жалпы шешімді береді. Коши есебінің қойылуына мысал

теңдеуінің жалпы шешімін табайық. Сәйкес сипаттаушы симметрия жүйесін құрайық: Осыдан интегралдарын табамыз. Бұл жағдайда жалпы шешім түрінде жазылады. Дифференциалдау арқылы бұл функцияның шешім болатынына көз жеткізу оңай.

15. Бірінші ретті дербес туындылы сызықты біртекті емес дифференциал теңдеудің жалпы шешімін табу... Біртексіз сызықты теңдеуді қарастырайық: (13)

Мұндағы, - функциялары кейбір облысында үздіксіз дифференциалданатын және бәрі бірдей нөлге тең емес деп есептелінеді:

Бұл теңдеуді біртекті сызықты түрге келтіру арқылы интегралдайды. Ол үшін шешімді айқындалмаған функция түрінде іздейді:

(14)

Мұндағы, - функциясын облысында үздіксіз дифференциалданатын және деп аламыз. Осы қатынасты кез келген бойынша дифференциалдайық: Осыдан 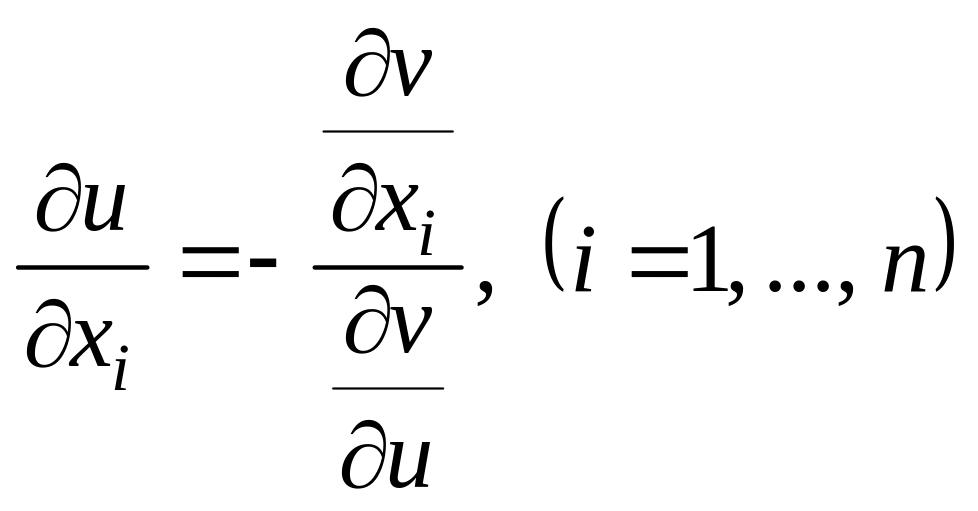(15)

(15) өрнекті (13) теңдеуге қойып, оны бөлшегіне көбейтсек,

(16)

теңдеуін аламыз. Бұл бойынша біртекті сызықты теңдеу. Сондықтан, алдыңғы пунктте көрсетілген тәсілді қолданамыз. Бұл теңдеудің сәйкес сипаттаушы жүйесі (17)

түрінде жазылады. Бұл жүйенің өзара тәуелсіз интегралдары - ге тең:

Бұл жағдайда (13) теңдеудің жалпы шешімі

(18) түрінде жазылады. Шешімді анықталмаған түрде іздеп отырғанымызды ескерсек, (19)

қатынасын аламыз. Осындағы -ды арқылы өрнектеуге мүмкін болса, ол функция (13) теңдеудің шешімі болады.

Бұл жерде арнайы шешімдер де болуы мүмкін. Ондай шешімдер сол уақытта пайда болады, егер (14) тепе-теңдік тек болғанда ғана орындалса. Коши есебінің қойылуына мысал теңдеуінің жалпы шешімін құрайық. Сәйкес жүйесінің екі тәуелсіз интегралдары оңай табылады: Жалпы шешім айқындалмаған түрде жазылады: Осы қатынасты екінші аргументі бойынша шешсек, түріндегі шешім аламыз.