5.Коши есебінің бар және жалғыз болуы туралы теорема.V-vі кезеңін дәлелдеу.

Теорема-1. Егер функциясы облысында төмендегідей екі шартты қанағаттандырса:

1. екі аргументі бойынша үздіксіз, сондықтан ол шектелген:

2) Аргументі бойынша Липшиц шартын қанағаттандырады, яғни кез келген екі нүкте үшін

(4)

теңсіздігі орындалады, , онда бастапқы (2) шартты қанағаттандыратын, аралығында анықталған үздіксіз дифференциалданатын жалғыз ғана шешім бар болады.

Коши есебінің шешімінің жалғыздығын дәлелдеу үшін алдымен Гронуолл леммасын келтірейік.

Лемма. Кейбір аралығында үздіксіз функциялары және тұрақты саны үшін (13) теңсіздігі орындалса, онда одан мынандай теңсіздік алуға болады: (14)

Дәлелдеуі.(13) теңсіздікті оң жағындағы қосындыға бөлейік :

Екі жағында оң функциясына көбейтіп, -ден -ға дейін интеграл алайық:

Мұнда бөлшектің алымы бөлімінің туындысы екенін ескерсек, онда

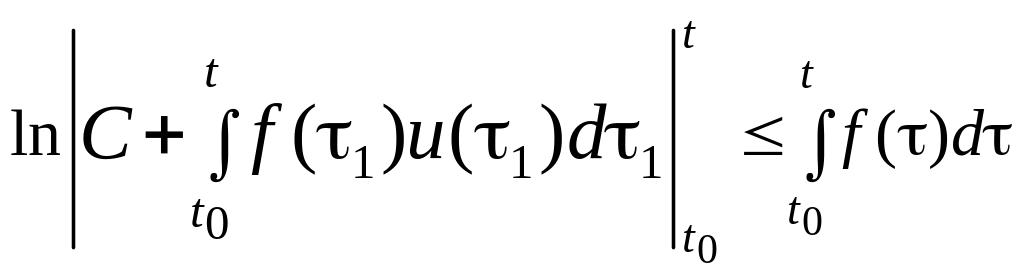
Осыдан ,

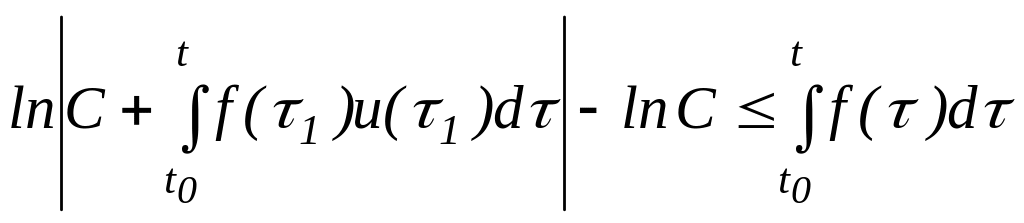
Потенциалдап, одан соң берілген (13) теңсіздікті пайдалансақ, (14) теңсіздікке келеміз ( болғанда лемманы дәлелдеу үшін интегралдың бағытын өзгертсе, жеткілікті).

Енді осы (14) теңсіздікті пайдаланып, шешімнің жалғыздығын көрсетейік.

Айталық, (x) және ψ(x) функциялары әртүрлі екі шешім болсын:

,

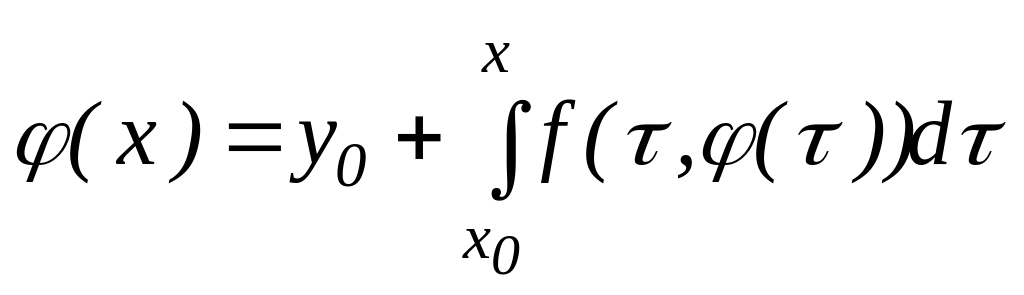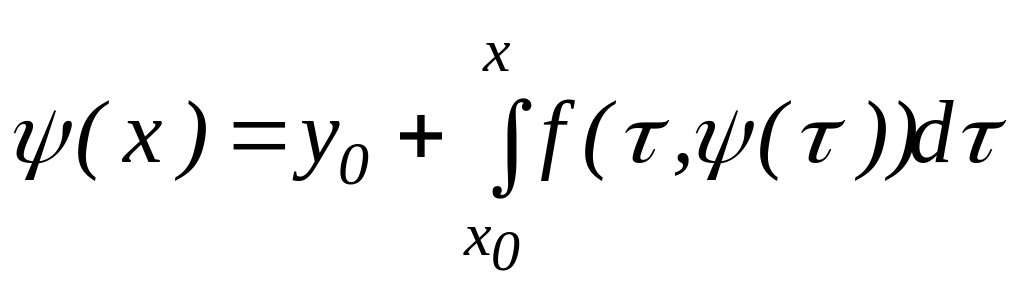
Осы шешімдердің айырмасын бағалайық:

Мұнда , f(x)=L, C=0 екенін ескерсек, (14) теңсіздіктен теңдігі шығатынын көреміз, яғни (x)=ψ(x), .

Сонымен, Пеано кесіндісінде Коши есебінің тек жалғыз ғана шешімі бар екені толық дәлелденді.

6. Жоғарғы ретті дифференциалдық теңдеу үшін қойылған Коши есебі шешімінің жалғыз және бар болуы туралы теорема. Жалпы шешім.

Жоғарғы ретті жәй дифференциалдық теңдеудің туынды бойынша шешілмеген түрі былай жазылады: (1)

Мұндағы, -тәуелсіз айнымалы, -белгісіз функция, ал - белгісіз функцияның туындылары . - кейбір облысында анықталған нақты үздіксіз функция.

Егер (1) қатынас жоғарғы туындысы бойынша шешілсе, онда былай жазамыз: (2)

Мұндағы, - функциясы кейбір облысында анықталған үздіксіз функция деп есептелінеді.

Анықтама-1. аралығында анықталған функциясы (2) теңдеудің осы аралықтағы шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:

функциясы аралығында рет дифференциалданатын болса;

;

.

Айқындалмаған (1) теңдеудің де шешімін осы түрде анықтауға болады.

Анықтама-2. аралығында анықталған функциясы (1) теңдеудің осы аралықтағы шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:

функциясы аралығында рет дифференциалданатын болса;

;

.

Жоғарғы ретті теңдеу үшін Коши есебі былайша қойылады: (2) теңдеудің барлық шешімдерінің ішінен

(3)

шартын қанағаттандыратын шешімді табу керек. Мұндағы, сандарын бастапқы мәндер, ал (3) шартты бастапқы шарт деп атайды. Әрине, мұнда .

Коши есебіне жауапты төмендегідей теорема айқындайды.

Теорема-1. Егер функциясы бастапқы нүктені қамтитын ашық облысында үздіксіз болса, ал оның кез келген шектелген тұйық ішкі бөлігінде векторы ьойынша Липшиц шартын қанағаттандыратын болса, онда Коши есебінің кейбір кішірейген аралықта анықталған жалғыз ғана шешімі болады.