РЕШЕНИЕ ЗАДАЧ ВЫПОЛНЕНО В СИСТЕМЕ СИ.

Задача № 27.

Для выпуска нефти из нефтехранилища устроены квадратное отверстие размером 100×100 мм и откидной клапан под углом .

Определить усилие Р, которое нужно приложить к цепи для открытия клапана, если глубина его расположения . Относительный вес нефти 0,9.

Дано:

Найти:

Решение

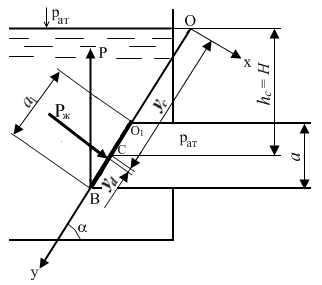
Рис. 1.

Выберем систему координат как показано на рис. 1. Начало системы координат O расположим на уровне жидкости в резервуаре.

Сила гидростатического давления жидкости на клапан

, (1)

где – гидростатическое давление в центре тяжести клапана, – глубина погружения центра тяжести клапана, – площадь смоченной поверхности клапана

Из рисунка 1 видно, что клапан представляет собой прямоугольник со сторонами и . Тогда площадь смоченной поверхности клапана

, (2)

Как видно из рис. 1, глубина погружения центра тяжести клапана

. (3)

Подставляя выражения (2) и (3) в формулу (1) получим

.

Вычислим значение силы

.

Линия действия силы находится ниже центра тяжести клапана. Расстояние между центром тяжести клапана и точкой приложения силы , отсчитываемое вдоль поверхности клапана (рис. 1), можно определить по формуле

(4)

где – центральный момент инерции клапана, – расстояние от точки О до центра тяжести клапана.

Из рисунка 1 видно, что расстояние от центра тяжести клапана до уровня жидкости, отсчитываемое вдоль поверхности клапана,

. (5)

Так как клапан имеет форму прямоугольника со сторонами и , то момент инерции клапана

. (6)

Подставляя выражения (2), (5) и (6) в формулу (4), получим

.

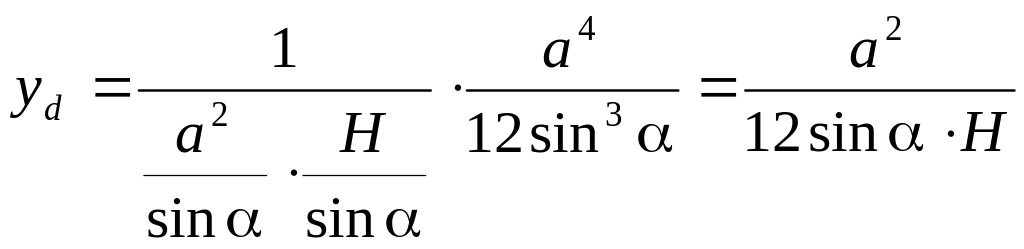
Для определения силы Р, необходимой для открытия клапана, составим уравнение моментов относительно точки O₁:

,

учитывая, что , получим

,

откуда

.

Проведем вычисления

.

Ответ: .

Задача №68

Найти скорость течения воды в трубе, если показание ртутного манометра, присоединенного к трубке Пито и к отверстиям статического давления, равно .

Дано:

Найти:

Решение:

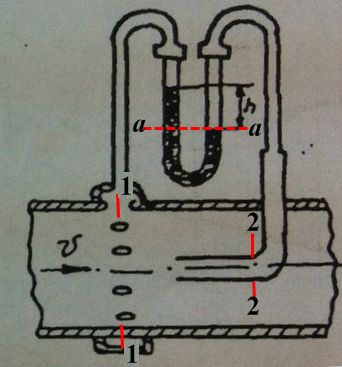
Рис. 1.

Выберем сечения 1–1 и 2–2, как показано на рис. 1. Плоскость сравнения совместим с осью трубопровода.

Запишем уравнение Бернулли для сечений 1–1 и 2–2 без учета потерь напора, принимая за плоскость сравнения ось трубы:

, (1)

где – плотность воды

В рассматриваемом случае , , , где – средняя скорость воды в трубе. Скорость воды в трубке Пито .

Подставляя значения величин в уравнение (1), получим

,

откуда

. (2)

Запишем условие равновесия в ртутном манометре относительно плоскости а – а

,

где – плотность ртути.

Тогда

. (3)

Подставляя уравнение (3) в формулу (2), получим

,

откуда скорость v воды в трубе

.

Ответ: .

Задача №1.

Определить разность давлений в двух сечениях трубы, по которой течет вода, по показанию ртутного дифференциального манометра, если . Ответ дать в метрах водяного столба.

Дано:

Найти:

Решение:

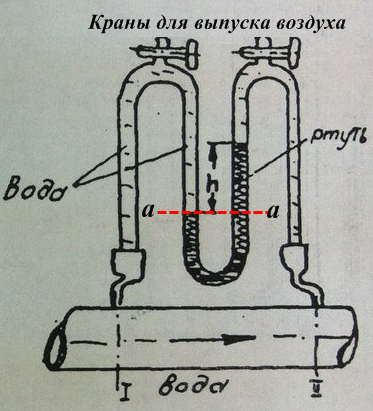
Рис. 1.

Запишем условие равновесия жидкости в ртутном дифференциальном манометре относительно плоскости а – а

.

где и – соответственно удельный вес воды и ртути.

Тогда

,

.

Выразим в метрах водного столба h_в

м. вод. ст.

Выразим в метрах ртутного столба h_рт

м. рт. ст.

Ответ: 4,41 м. вод. ст; 0,324 м. рт. ст.

Задача №107.

Вода протекает из напорного бака, где давление воздуха , в открытый резервуар по короткому трубопроводу, составленному из трех участков различного диаметра. Определить расход воды Q, если высоты уровней и , площади поперечных сечений ; ; . Учесть потери на вход на удар и при внезапном сужении.

Дано:

Найти:

Решение:

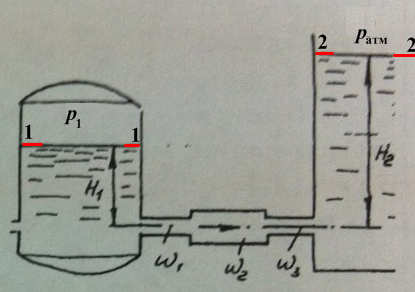
Рис. 1.

Выберем сечения 1–1 по свободной поверхности жидкости в баке, сечение 2–2 – по свободной поверхности жидкости в открытом резервуаре, как показано на рис. 1. Плоскость сравнения совместим с сечением 1–1.

Составим уравнение Бернулли для сечений 1–1 и 2–2

, (1)

где – плотность воды.

В рассматриваемом случае , .

Так как уровни жидкости в баке и резервуаре поддерживаются постоянными, то .

Подставив все значения в уравнение Бернулли (1), получим

, (2)

Так как трубопровод короткий, то потерями на трение по длине пренебрежем, тогда потери напора будут обусловлены только потерями в местных сопротивления.

Определим потери напора в местных сопротивлениях. По условию задачи необходимо учесть потери на вход на удар и при внезапном сужении.

Потери напора на вход в трубу

,

где – коэффициент сопротивления при входе в трубу из напорного бака, v₃ – средняя скорость воды на первом участке трубопровода.

Потери напора при внезапном сужении

,

где – коэффициент сопротивления при внезапном расширении.

Потери напора на вход в резервуар из трубы (т.е. при выходе из трубы)

,

где – коэффициент сопротивления при выходе из трубы в резервуар, v₃ – средняя скорость воды на третьем участке трубопровода.

Суммарные потери напора

.

Согласно уравнению расхода

,

откуда

.

Тогда

,

. (3)

Подставляя(3) в формулу (2), получим

,

откуда средняя скорость воды на первом участке трубопровода

.

Вычислим расход воды

.

Ответ: .