19.Неоднородные слау. Теорема о представлении решения неоднородной системы. Алгоритм решения неоднородных систем.

Выясним, чем отличается решение произвольной неоднородной системы алгебраических уравнений от решения однородной системы.

Определение. Однородная система линейных алгебраических уравнений называется соответствующей неоднородной системе, если коэффициенты при неизвестных у них одинаковые, а свободные члены неоднородной системы заменены нолями.

Рассмотрим произвольную совместную неоднородную систему линейных алгебраических уравнений:

Пусть у нее в общем случае , то есть имеется бесконечное множество решений.

Теорема 4.1. Сумма любого решения неоднородной системы линейных алгебраических уравнений с любым решением соответствующей ей однородной системы является решением неоднородной системы.

Доказательство. Возьмем произвольное решение неоднородной системы

и произвольное решение соответствующей ей однородной системы

. Рассмотрим их сумму .

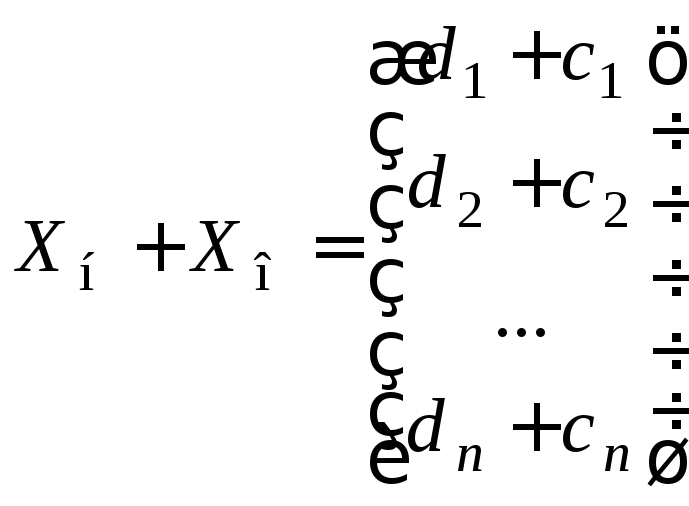Если данная сумма является решением неоднородной системы, то она должна превратить в тождество любое ее уравнение:

что и требовалось доказать.

Теорема 4.2. Разность любых двух решений неоднородной системы линейных алгебраических уравнений является решением соответствующей однородной системы.

Доказательство. Возьмем два произвольных решения неоднородной системы линейных алгебраических уравнений:

и . Составим их разность.

Подставим полученную разность в любое уравнение неоднородной системы:

Так как левая часть уравнения обратилась в ноль, значит, является решением однородной системы, что и требовалось доказать.

Из теоремы 4.2 следует, что если , то. Иначе говоря, взяв какое-то одно решение неоднородной системы линейных алгебраических уравненийи прибавляя к нему разные решения соответствующей однородной системы, получим разные решения неоднородной системы, что подтверждается теоремой 4.1.

Следствие. Общее решение неоднородной системы линейных алгебраических уравнений равно сумме какого-то частного ее решения и общего решения соответствующей однородной системы.

20.Определение линейного (векторного) пространства. Примеры линейных пространств (лп).

Лине́йноепростра́нство, или ве́кторноепростра́нство — основной объект изучения линейной алгебры

Определение

Линейное, или векторное пространство над полем P — это непустое множество L, на котором введены операции

сложения, то есть каждой паре элементов множества ставится в соответствие элемент того же множества, обозначаемый и

умножения на скаляр (то есть элемент поля P), то есть любому элементу и любому элементу ставится в соответствие элемент из , обозначаемый .

При этом на операции накладываются следующие условия:

, для любых (коммутативность сложения);

, для любых (ассоциативность сложения);

существует такой элемент , что для любого (существование нейтрального элемента относительно сложения), в частности L не пусто;

для любого существует такой элемент , что (существование противоположного элемента).

(ассоциативность умножения на скаляр);

(умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).

(дистрибутивность умножения на вектор относительно сложения скаляров);

(дистрибутивность умножения на скаляр относительно сложения векторов).

Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.

Примеры

Нулевое пространство, единственным элементом которого является ноль.

Пространство всех функций с конечным носителем образует векторное пространство размерности равной мощности X.

поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.

Любое поле является одномерным пространством над собой.

-----------------------------------

Определение и примеры линейных пространств (ЛП).

Опр.: Множество V≠Ø (произвольной природы) называется линейным пространством (ЛП), если для элементов этого множества V определены 2 операции:

1) Для любой упорядоченной пары элементов x,yV x+yV

(внутренняя операция сложения элементов между собой)

2) Для любого αR и для любого xV α•xV (внешняя операция умножения элементов на скаляры),

обладающие 8 свойствами (аксиомами ЛП)

1.x+y = y+x

2.x+(y+z) = (x+y)+z

3. ӨV: x+Ө = x

4. xV x’V: x+x’ = Ө

5.1•x = x

6.(αµ)x = α(µx)

7. (α+µ)x = αx+µx

8. α(x+y) = αx+αy

x,y,zV и α,µR

Утв.:

1. ! ӨV: x+Ө = x xV

2. xV !x’V: x+x’ = Ө

3. 0•x = Ө xV

4. (-1)•x = x’ xV

Доказательство:1. Пусть Ө₁ и Ө₂ – два ненулевых элемента в V

Тогда Ө₁ =³ Ө₁+Ө₂ =¹ Ө₂+Ө₁ =­³ Ө₂, т.е. Ө₁=Ө₂

2. Пусть для некоторого элемента xV два противоположных элементаx’ и x’’, т.е.

x+x’ = Ө и x+x’’ = Ө, тогда

x’ =³ x’+Ө = x’+(x+x’’) =² (x’+x)+x’’ =¹ (x+x’)+x’’ = Ө+x’’ = x’’,

т.е. x’=x’’

3. 0•x = 0•x+Ө = 0•x+(x+x’) = (0•x+x)+x’ = (0+1) •x+x’ = 1•x+x’ = x+x’ = Ө xV

4. x+(-1)•x = 1•x+(-1) •x = (1+(-1)) •x = 0•x = Ө xV

x’ = (-1)•x

Примеры линейный пространств:

1. V1,V2,V3

2. Rⁿ = {x = (x₁,x₂,…,x_n): x_kR, k=}

n-мерное вещественное пространство

x+y ≡ (x₁+y₁; x₂+y₂;…;x_n+y_n)

λx ≡ (λx₁, λx₂,…, λx_n), λR

3. ( R) – множество всевозможных матриц с вещественными элементами фиксированного размераmxn, с линейным определителем, введенным ранее.

4. P_n[x] – множество всех многочленов степени ≤n переменной x с естественными операциями.

5. C[a,b] – множество всех непрерывных на [a,b] функций

+ то же, что и в 4.

6. Множество всех решений ОСЛАУ.