15.Элементарные преобразования слау. Метод Гаусса исследования слау.

Элементарными преобразованиями над системой линейных алгебраических уравнений:

- перестановку уравнений;

- умножение уравнения на ненулевую константу;

- сложение одного уравнения с другим, умноженным на некоторую константу.

Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:

Теорема (об эквивалентности систем уравнений при элементарных преобразованиях).

Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей.

Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Метод Гаусса решения СЛАУ

Пусть RangA=r0, m0. Тогда первый шаг:

Можем считать, что а₁₁0 (иначе добьёмся этого с помощью элементарных преобразований 1)-3) и, возможно, переобозначив переменные)

(*)A⁽¹⁾•=⁽¹⁾

Если r1, m2, то совершим второй шаг (считаем а₂₂0):

A⁽²⁾•=⁽²⁾ после преобразований 1)-3)

И так далее. На r-ом шаге получаем СЛАУ A^(r)•=^(r), равносильную СЛАУ(*) (множества решений этих СЛАУ совпадают)

АА^(r), RangA=RangA^(r)=r

(А|) (A^(r)|^(r)), Rang(А|)=Rang(A^(r)|^(r))

Поменяем СЛАУ (а вместе с ней и СЛАУ(*))

совместна <=> .

В таком случае отбрасываем m-r последних уравнений и приходим к СЛАУ:

16.Критерий совместности слау (теорема Кронекера-Капелли).

теорема Кронекера–Капеллы

СЛАУ А : x = b – совместна  Rang A =RANG(A/b)

Частный случай:

При r=n СЛАУ(*) имеет единственное решение т.е. является определенной т.к. свободные неизвестные отсутствуют.

Рассматриваем ОСЛАУ x = 0

когда совместна имеет решение х=0 называемое тривиальным.

18. Понятие фср однородной системы. Теорема о представлении общего решения через фср.

Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.

Однородные системы

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

Теорема (о линейном решении однородных систем). Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.

Сформулируем теорему, которая позволит дать основное определение:

Теорема (о структуре общего решения). Пусть , тогда:

• если , где 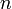— число переменных системы, то существует только тривиальное решение;

если , то существует линейно независимых решений рассматриваемой системы: , причём её общее решение имеет вид: , где — некоторые константы.

Пусть дана однородная система (1), тогда набор векторов размера называется фундаментальной системой решений (ФСР) (1), если:

—решения системы (1);

линейно независимы;

.

Теорема (о ФСР). Пусть ранг основной матрицы , где n— число переменных системы (1), тогда:

• ФСР (1) существует: ;

• она состоит из 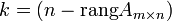векторов;

• общее решение системы имеет вид .

Замечание: Если , то ФСР не существует.

Пример

Решим систему

Перепишем её в матричном виде:

Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:

Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует линейно независимых решения системы.

Перепишем полученную систему в виде уравнений:

Возьмём х1и х2в качестве главных переменных. Тогда:

Подставим по очереди единицы в качестве одной из свободных переменных: Х3и Х4.

Тогда общее решение рассматриваемой системы может быть записано так:

,

а вектора составляют фундаментальную систему решений.