12.Элементарные преобразования матриц. Вычисление ранга матрицы методом элементарных преобразований.

Вычисление ранга методом элементарных преобразований:

1.

2.

3. (поменять местами)

То же самое и для столбцов (4-6).

А→В (от А к В пришли с помощью элементарных преобразований)

Поскольку элементарные преобразования обратимы, то чаще пишут А~В (доказательство элементарных преобразований сразу вытекает из теоремы о ранге матрицы, для 2. очевидно)

Утверждение 1.

Если А~В, то Rang A=Rang B.

Утверждение 2.

А≠, АєM_m•n

С помощью элементарных преобразований 1-3,6 матрицу А можно привести к трапециевидной форме.

АС=

m-r нулевых строк

=> Rang A=Rang C=r

Доказательство.

А≠0 => a_ij≠0a_ij попадет на место a₁₁он стал равным 1.

Далее, получаем в первом столбце нули, совершая элементарные преобразования 1,2.

А,

если не равно 0, процесс продолжаем, пока не получим C.

13. Собственные значения и собственные элементы матриц.

Если при действии линейного оператора f на ненулевой век­тор х получается тот же вектор х, умноженный на какое-то число Я, то такой вектор х называется собственным вектором линейного оператора f: f(x)= λx. Число λ называется собственным значением.

Нахождение собственных векторов и собственных значений

В матрице А порядка п линейного оператора f на главной диаго­нали вычитается число λ. Определитель полученной матрицы при­равнивается нулю, т. с. det(A — λЕ) = 0. Это характеристическое урав­нение. Его решения и есть собственные значения λ_1, λ2,, ..., λ_Л.

Для каждого λ_/: решается однородная система (A — λ_jE)X = 0, где

X=(х1 0=(0

.. ..

хn) 0).

Выражаем главные переменные через свободные переменные и методом бегущей единицы (поочередно одну свободную перемен­ную приравниваем единице, остальные свободные переменные при­равниваем нулю, находим значения главных переменных) получаем все собственные векторы, соответствующие собственному значению λj.

Собственные значения

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

det(A − λI) = 0,

являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Набор собственных значений λ1,..., λN матрицы A называется спектром A.

Спектр обладает разнообразными свойствами. В частности

det(A) = λ1×...×λN, Sp(A) = λ1+...+λN.

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (At = A), то ее собственные значения вещественны.

Собственные векторы

У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора vn нужно решить систему однородных уравнений

(A − λnI) vn = 0.

Она имеет нетривиальное решение, поскольку det(A − λnI) = 0.

Собственные вектора симметричной матрицы ортогональны.

14.Определение системы линейных алгебраических уравнений (СЛАУ), матричная форма записи. Квадратные СЛАУ, теорема Крамера.

Системы линейных алгебраических уравнений

Рассмотрим СЛАУ из m уравнений с n неизвестными

где а_ij – коэффициенты СЛАУ, i=, j=

b_i- свободные члены, i=

Найти: х_j – неизвестные, j=

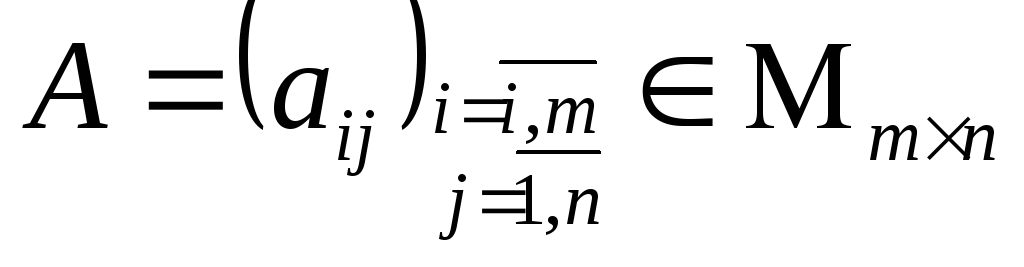
CЛАУ (*) называется:

1) Совместной, если она имеет хотя бы одно решение.

2) Несовместной, если она не имеет решения.

3) Определенной, если она имеет единственное решение.

4) Неопределенной, если она имеет более одного решения (потом поясним, что бесконечно много решений).

5) Однородной, если =

6) Неоднородной, если k=, b_k0 ()

Частное решение СЛАУ(*) - это такой упорядоченный набор чисел ₁,₂…._n, что при подстановке его в (*) вместо х₁….x_n получаем m верных равенств.

Общее решение СЛАУ(*) - это решение, содержащее несколько производных постоянных (параметров), такое, что любое частное решение СЛАУ(*) получается из общего, если зафиксировать специальным образом указание произвольных постоянных.

Система (*) называется квадратной если число m составляющих ее уравнений равно числу неизвестных n

Теорема Крамера.

Пусть СЛАУ(*) является квадратной, т.е. АМ_n и |А|0. Тогда (*) имеет единственное решение (является определенной), которое находится по формуле:

Х_к=, k=, где D_k=(₁, ₂,...,•_n+1,...,_n)

Доказательство:

Покажем, что =А^-1• – решение (*)

( А^-1, так как |А|Во0)

В самом деле, А•(А^-1•)=(А•А^-1)• = (единственное решение следует из единственности обратной матрицы)

Запишем

=A^-1•==>

X_k=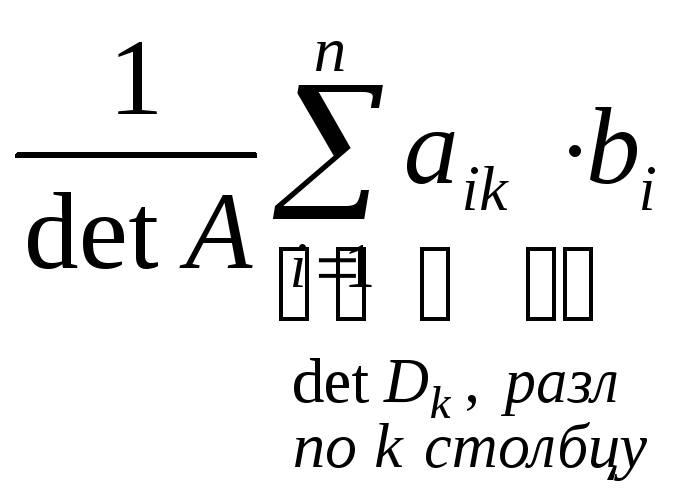

теорема Кронекера–Капеллы

СЛАУ А : x = b – совместна  Rang A =RANG(A/b)

Частный случай:

При r=n СЛАУ(*) имеет единственное решение т.е. является определенной т.к. свободные неизвестные отсутствуют.

Рассматриваем ОСЛАУ x = 0

когда совместна имеет решение х=0 называемое тривиальным.