
Еще шпоры по ЛинАл
.doc|
1. (1 из 3) Образ и ядро линейного оператора. Ранг и дефект линейного оператора. |
1. (2 из 3) Образ и ядро линейного оператора. Ранг и дефект линейного оператора. |
|
Пусть
Def:
Совокупность всевозможных векторов
вида
Def:
Совокупность всевозможных векторов
Утв:образ и ядро линейного оператора А являются подпространствами линейного пространства V. 1)
2)
Док-во: В самом деле в силу линейности оператора А имеем: 1)
2)
Пример: Пусть V – n мерное компл или вещ лин пр-во. 1)
Тождественный оператор
/ ядро состоит из единственного нулевого элемента /
2)
Нулевой оператор
|
3)
Рассмотрим оператор дифференцирования
Th (о сумме размерностей образа и ядра линейного оператора) : Пусть
A - линейный оператор,
действующий в линейном пространстве
V. Тогда сумма
размерностей образа и ядра оператора
равна размерности данного линейного
пространства, т.е.
Док-во: Пусть
Выберем
в пространстве V
произвольный базис
Но координаты именно этих векторов
стоят в столбцах матрицы
Рассмотрим ядро оператора А:
В выбранном базисе равенству
СЛАУ:
|
|
1. (3 из 3) Образ и ядро линейного оператора. Ранг и дефект линейного оператора. |
2. (1 из 1) Собственные значения и собственные векторы линейного оператора А. |
|
образующих ФСР. Поскольку неизвестными
данной системы являются координаты
векторов, составляющих KerA,
то отсюда заключаем, что dim(KerA)=n-r.
В результате получаем, что
Def: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора. Def:
Линейный оператор
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует. Док-во:
Если
Отсюда
Def:
Подпространство L
пространства V
называется инвариантным относительно
линейного оператора А, если
Th (об инвариантности образа и ядра линейного оператора): Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А. Док-во: 1)
Пусть
2) Пусть
|
Пусть
Def:
Число λ – наз-ся собств знач (с.з.)
лин опер А, если
Здесь
Th (Критерий существования собств знач лин оператора А): Для того, чтобы λ было собств знач линейного оператора А, необх и достаточно чтобы это число было корнем хар-ого ур-я оператора А. Док-во: Пусть
(1по критерию существования ненулевых решений однородной СЛАУ.) Правила нахождения с.з. и с.в. линейного оператора А. 1)
Выбираем в пространстве
2)
Находим все собственные значения как
корни характеристического уравнения
3)
Решая однородную СЛАУ
Def: Множество всех собственных значений оператора А называется спектром оператора А. |
|
3. (1 из 1) Свойства собственных значений и собственных векторов линейного оператора |
4. (1 из 2) Диагонализуемость линейного оператора. |
|
1)
Пусть
Док-во:
2)
Если
Док-во:
Будем доказывать методом математической
индукции. Так как
Подействуем
оператором A на
(*). Получим
Т.к.
3) Приведение матрицы к диагональному виду. |
Def: Квадр матрица А порядка n наз диагональной, если имеет вид: ... Def: Линейный оператор называется диагонализуемым, если в линейном пространстве существует базис, в котором матрица А данного линейного оператора имеет диагональный вид. Th 1: (критерий диагонализуемости матрицы линейного оператора). Пусть
Док-во: Необходимость: Пусть
в базисе
Достаточность:
Пусть базис
Th 2: (Дост усл диагонализуемости матрицы лин оператора). Пусть
dimV=n,
если линейный оператор
|
|
4. (2 из 2) Диагонализуемость линейного оператора. |
5. (1 из 2) Билинейные формы в лин пр-ве. Симметрич и кососимметрические билинейные формы. |
|
Док-во:
Пусть
Замечание
1: Обратная теорема неверна. В
качестве примера можно рассмотреть
тождественный оператор
Следствие:
Если все корни характеристического
уравнения
Док-во:
Доказательство вытекает из формулы
преобразования матрицы линейного
оператора
Замечание
2: Не для всякого оператора А
в пространстве V
существует базис, состоящий из
собственных векторов. Например,
линейный оператор А, матрица
которого в некотором базисе (е)
имеет вид
|
Пусть V – вещественное линейное пространство. Def:
Билинейной формой называется числовая
функция A(x,y)
2-х векторных аргументов x
и y ( 1) A(x+y,z)=A(x,z)+A(y,z) 2) A(x,y+z)=A(x,y)+A(x,z) 3) A(λx,y)= λA(x,y) 4)
A(x,
λy)= λA(x,y)
Пример 1: Пусть f(x) и g(y) - две линейные формы, т.е. линейные операторы, отображающие пространство V в числовое множество. Тогда A(x,y)=f(x)g(y) - билинейная форма. Пример 2: Скалярное производные 2-х векторов:
Получим теперь
выражение для билинейной формы в общем
виде, пусть
|
|
5. (2 из 2) Билинейные формы в лин пр-ве. Симметрич и кососимметрические билинейные формы. |
6. (1 из 2) Матрица билинейной формы и ее преобразование при переходе к новому базису. |
|
Def:
Билинейная форма A(x,y)
называется симметрической
(кососимметрической), если
Замечание
1: Всякая симметрическая билинейная
форма A(x,y)
однозначно определяется своими
значениями для совпадающих аргументов.
В самом деле:
Замечание
2: Если A(x,y)
- симметрическая билинейная форма, то
ее матрица
|
Def:
Матрица
Преобразование матрицы билинейной формы при переходе от одного базиса к другому.
Пусть A(x,y)
- билинейная форма в вещественном
линейном пространстве V.
Th:
Док-во: Вспомним, что
Запишем:
|
|
6. (2 из 2) Матрица билинейной формы и ее преобразование при переходе к новому базису. |
7. (1 из 2) Квадр формы в лин пр-ве. Матрица квадр-й формы и ее преобраз-ие при переходе к новому базису. |
|
Th:
Пусть в линейном пространстве V
фиксированный базис
Док-во:
Фиксируем базис
Обратно,
если дана матрица
Следствие.
Представление
|
Пусть A(x,y) - симметричная билинейная форма в вещественном линейном пространстве. Def: Квадратичной формой A(x,x) называется числовая функция одного векторного аргумента x, которая получается из симметричной билинейной формы A(x,y), если y=x. Утв:Для
любой квадратичной формы
Def: Матрицей квадратичной формы
A(x,x)
называется матрица A
Пусть
Если в последней сумме выделить
слагаемые с i=j
и учесть, что
Пример: Дана квадратичная
форма
Записать
матрицу квадратичной формы:
Замечание: Матрица квадратичной формы, как и билинейной, преобразуется по закону:
|
|
7. (2 из 2) Квадр формы в лин пр-ве. Матрица квадр-й формы и ее преобраз-ие при переходе к новому базису. |
8. (1 из 3) Приведение квадратичной формы к каноническому виду методом Лагранжа. |
|
Def: Базис(e),
в котором матрица Ae
квадратичной формы A(x,x)
принимает диагональный вид
Ранее рассматривался вопрос о диагонализуемости матрицы линейного оператора, теперь обратимся к вопросу о диагонализуемости матрицы квадратичной формы. В частности, рассмотрим вопрос о существовании канонического базиса.
Известно, что при переходе от одного
базиса к другому координаты вектора
изменяются следующим образом: если
Def: Преобразование
координат
Тогда каждому преобразованию базиса можно сопоставить невырожденное линейное преобразование координат и наоборот. Поэтому вопрос о существовании канонического базиса можно заменить вопросом о существовании невырожденного линейного преобразования координат. Заметим
также, что если
Вывод: Суперпозиция невырожденных преобразований координат также является невырожденным преобразованием. Причем матрица результирующего преобразования равна произведению матриц, приводящих к этому результирующему преобразованию. |
Th (Лагранжа): Всякая квадратичная
форма A(x,x)
в вещественном линейном пространстве
V при помощи
невырожденного линейного преобразования
координат может быть приведена к
каноническому виду (диагональной
форме).
Док-во: (по методу математической
индукции) по размерности пространства
V , в котором действует
1) Пусть dimV=1
и e1 - базис в
пространстве V, тогда
2) Пусть dimV=m
и для всех
3) Докажем указанное утверждение при m=n.
Пусть
Возможны два случая: а)
Хотя бы одно из чисел
|
|
8. (2 из 3) Приведение квадратичной формы к каноническому виду методом Лагранжа. |
8. (3 из 3) Приведение квадратичной формы к каноническому виду методом Лагранжа. |
|
Выполним невырожденное преобразование координат:
Получаем:
|
Если T – матрица
результирующего преобразования
координат, т.е.
б) Пусть теперь все диаг элементы
Замечание 1: Изложенный в док-ве последней теоремы метод приведения квадратичной формы к канонич виду наз-ся методом Лагранжа и фактически сводится к выделению полных квадратов.
Замечание 2:
Преобразование переменных, приводящее
квадратичную форму A(x,x)
к каноническому виду, а значит, и сам
канонический базис
|
|
9. (1 из 3) Нормальн вид квадр формы. Закон инерции квадр форм. Знакоопред квадр формы. Кр Сильвестра. |
9. (2 из 3) Нормальн вид квадр формы. Закон инерции квадр форм. Знакоопред квадр формы. Кр Сильвестра. |
|
Если после приведения квадратичной
формы A(x,x)
к каноническому виду
Как отмечалось в Замечании 2 предыдущего параграфа, приведение квадратичной формы к каноническому виду можно осуществить различными преобразованиями координат (канонический вид квадратичной формы неоднозначен), однако, с точностью до нумерации переменных получается один и тот же нормальный вид квадратичной формы. Это подтверждает следующая теорема. Th (закон инерции квадратичной формы): Число положительных коэффициентов в нормальном виде квадратичной формы называемое положительным индексом инерции; число отрицательных коэффициентов называемое отрицательным индексом инерции и число нулевых коэффициентов называемое дефектом квадратичной формы являются инвариантами, т.е. не зависят от базиса, в котором данная квадратичная форма принимает нормальный вид.
Док-во: Пусть имеются 2-а базиса,
в которых квадратичная форма A(x,x)
принимает нормальный вид:
|
Здесь полагаем, что
Будем доказывать методом от противного,
т.е. предполагаем, что
Рассмотрим
следующие пространства:
Точно также
Аналогично доказываются другие 3-и
случая:
Def: Квадратичная форма A(x,x)
в вещественном линейном пространстве
V называется
положительно определенной, если
|
|
9. (3 из 3) Нормальн вид квадр формы. Закон инерции квадр форм. Знакоопред квадр формы. Кр Сильвестра. |
10. (1 из 2) Определение и примеры евклидовых и унитарных пространств. |
|
Квадратичная форма A(x,x)
называется отрицательно определенной,
если
Пусть
Рассмотрим матрицу
Главными минорами матрицы
Th (критерий Сильвестра знакоопределенности квадратичной формы):
Квадратичная форма A(x,x)
является положительно определенной
тогда и только тогда, когда все числовые
миноры положительны, т.е.
Квадратичная форма A(x,x)
является отрицательно определенной
тогда и только тогда, когда знаки
главных миноров чередуются, т.е.
При любой другой комбинации знаков главных миноров знак квадратичной формы не определен. Док-во: (Без доказательства).
|
Def: Вещественное линейное пространство V называется Евклидовым (обозначается Е), если:
I. имеется правило
согласно которому для любых
II. Указанное
правило, удовлетворяющее следующим
аксиомам
1)
2)
3)
4)
Def: Комплексное линейное пространство V называется унитарным (обозначается U), если:
I. имеется правило
согласно которому для любых
II. указанное
правило удовлетворяет следующим
аксиомам:
1)
2)
3)
4)
Следствие:
1)
2)
|
|
10. (2 из 2) Определение и примеры евклидовых и унитарных пространств. |
11. (1 из 2) Норма в евклидовом и унитарном пространствах. |
|
Примеры Евклидовых пространств (Е).
1) Множество всех геометрически
свободных векторов, если
2) Пространство An,
в котором
3) В пространстве An
можно положить
4) Пространство C[a,b],
в котором
Пример унитарного пространства (U).
Пространство An,
в котором
|
Пусть V=E (или V=U) Def:
Нормой (или длиной) элемента
Свойства нормы: Из свойств скалярного произведения сразу следует:
1)
2)
Док-во:
3) Неравенство Коши-Буяковского
Док-во: 1.
Пусть
а)
x
б)
С
другой стороны,
|
|
11. (2 из 2) Норма в евклидовом и унитарном пространствах. |
12. (1 из 1) Общий вид скалярного произведения в евклидовом и унитарном простр-вах. Матрица Грама. |
|
2.
Пусть
Пусть Пусть
4) Неравенство треугольника
Док-во: Используя неравенство Коши-Буяковского
|
Пусть 1)
Пусть Поскольку
Def: Матрица
называется
матрицей Грама базиса
2)
Для евклид. пространства
|
|
13. (1 из 2) Ортонормированный базис. Процесс ортогонализации по Гильберту — Шмидту. |
13. (2 из 2) Ортонормированный базис. Процесс ортогонализации по Гильберту — Шмидту. |
|
Def:
Базис
Здесь Th:
Система попарно ортогональными
ненулевых элементов
Док-во:
Выяснм усл-я выполн равенства
Для этого обе части данного равенства умножаем скалярно на один из элементов данной системы
Отсюда
следует, что
Итак,
для ОНБ элементы матрицы Грама равны
Th Гильберта-Шмидта (об ортогонализации базиса): Во
всяком
Док-во: ]
|
1)
Если имеется один вектор
2)
теперь предположим, что утверждение
доказано для
3)
Рассмотрим вектор
здесь
Выберем
Для
этого равенство (*) умножаем скалярно
на
Таким
образом, если
Замечание:
Алгоритм построен ОНБ по формулам
|
|
14. (1 из 2) Ортг доп-е подпр-ва унитар и евкл пр-ва. Th о представл унитарн пр-ва в виде прям сум лин подпр-в. |
14. (2 из 2) Ортг доп-е подпр-ва унитар и евкл пр-ва. Th о представл унитарн пр-ва в виде прям сум лин подпр-в. |
|
Def:
Два подпространства
Lem
1: Если
Док-во:
Пусть
Пусть
Def:
Ортогональн доп-ем
Пример:
V
Утв:: Ортогональное
дополнение
Док-во:
В самом деле,
Lem
2 (критерий): ]
Док-во:
Необходимость: Пусть
|
Достаточность:
Th: Унитарное
(евклидово) пространство
Док-во: Пусть
Возьмем
произвольный в-р
следовательно по Лемме 2
следовательно по Лемме 1
Следствие 1:
Док-во: Доказательство
следует из теоремы 2 § 5 гл. III
(Пусть V – сумма
подпространств V1
и V2, тогда
|
|
15. (1 из 3) Линейные, полуторалинейные и билинейные формы в евклидовом и унитарном пространствах. |
15. (2 из 3) Линейные, полуторалинейные и билинейные формы в евклидовом и унитарном пространствах. |
|
Def: Линейной
формой в линейном пространстве V
(унитарном или евклидовом) называется
числовая функция f(x)
векторного аргумента х, которая
удовлетворяет следующим условиям ( 1.f(x+y)=f(x)+f(y) 2.f( В
евклидовом пространстве Е линейная
форма принимает действительные
значения (т.е. f:E Th (о представлении линейной формы): Пусть
f(x): Док-во:
Пусть
Докажем
единственность элемента h
методом от противного , т.е. пусть
существует еще один элемент
Следствие:
Если
Замечание:Аналогичная теорема верна и для евклидова пространства Е. |
Ранее была введена билинейная форма в вещественном пространстве. Тогда можно говорить о билинейной форме в евклидовом пространстве. Её аналогией в унитарном пространстве является полуторалинейная форма. Def: Комплексно-значная
числовая функция B(x,y)
называется полуторалинейной формой
в унитарном пространсте U,
если
1. B(x+у,z)=B(x,z)+B(y,z). 2. B(x,y+z)=B(x,y)+B(x,z). 3.
B( 4.
B(x, Def: Полутаролинейная
форма B(x,y)
называется эрмитовой (эрмитовосиметрической),
если
Замечание: В евклидовом пространстве эрмитовость переходит в симметричность: B(x,y)=B(y,x), здесь B(x,y) – симметрическая билинейная форма. Пусть B(x,y) – полуторалинейная форма в унитарном пространстве U,
Тогда
B(x,y)= Def: Матрица
матрицей полуторалинейной
формы B(x,y)
в базисе
|
|
15. (3 из 3) Линейные, полуторалинейные и билинейные формы в евклидовом и унитарном пространствах. |
16. (1 из 2) Сопряженный оператор и его свойства. Матрица сопряженного оператора. |
|
B(x,y)= Th (о представлении полуторалинейной формы): Пусть
B(x,y)
- полуторалинейная форма в унитарном
пространстве U. Тогда
Док-во: При
фиксированном
Докажем линейность оператор А. С одной
стороны B(x,y+z)=
B(x,y)+
B(x,z)=(х,Ау)+
(х,Аz)=(x,Ay+Az).
С другой стороны B(x,y+z)=
(x,A(y+z))
(по определению полутаролинейной
формы), откуда получаем (x,Ay+Az)=
(x,A(y+z)) Замечание: Аналогичная теорема верна и для билинейной формы в евклидовом пространстве Е. |
Пусть A: VV – линейный оператор, где V=U или V=E. Def:
Оператор
Th:
Каждый линейный оператор A
имеет единственный сопряженный
оператор
Док-во:
(для V=U)
Замечание: Аналогично теорема доказывается и для V=E. Свойства сопряженного оператора: 1.
2.
3.
4.
5.
Если существует
6.
Если подпространство
Доказательства свойств (V=U): 1)
2)
= 3)
|
|
16. (2 из 2) Сопряженный оператор и его свойства. Матрица сопряженного оператора. |
17 (1 из 2) Нормальный оператор и его свойства. |
|
4)
5)
6)
Пусть существует
Пусть
По
определению матрицы линейный оператор
Итак,
|
Def:
Лин. оператор A,
действующий в унитарном U
(евклидовом E) пр-ве
наз-ся нормальным, если
Def:
Квадратная матрица
Свойства:
Пусть A: U
U – лин. оператор, при
этом
1)
Док-во:
Следствие:
2)
Если А – нормальный оператор, то
Док-во:
3)
Если l - собственный
вектор нормального оператора А,
отвечающий собственному значению λ,
то l - также собственный
вектор оператора А*,
отвечающий собственному значению
Док-во: Пусть
l - собственный вектор
нормального оператора А, отвечающий
собственному значению λ, т.е. Al=λl
или
|
|
17. (2 из 2) Нормальный оператор и его свойства. |
18. (1 из 1) Самосопряженный оператор и его свойства. |
|
4) Собственные векторы нормального оператора А, отвечающие различным собственным значениям, ортогональны. Док-во: Если
5)
Пусть
Док-во: Необходимость:
Пусть А – нормальный оператор,
т.е.
Достаточность: ]
|
Def:
Линейный оператор A,
действующий в унитарном U
(евклидовом E) пр-ве
называется самосопряженным,
если
Def:
Квадратная матрица
Свойства:
Пусть
1)
Пусть
Док-во: Аналогично док-ву свойства 5 нормальных операторов. # 2) Все собственные значения самосопряженного оператора, действующего в унитарном пространстве – вещественны. Док-во: Пусть
Следствие: Все собственные значения эрмитовой матрицы, вещественны (т.к. самосопряженному оператору в ОНБ отвечает эрмитова матрица). 3) Собственные векторы самосопряженного оператора, отвечающие различным собственным значениям, ортогональны. Док-во: Следует из св-ва 4 нормальных операторов, т.к. самосопряженный оператор является частным случаем нормального оператора. # 4)
Если подпространство
Док-во: Следует
из свойства 6 сопряженных операторов
и из того, что
|
|
19. (1 из 1) Унитарный (ортогональный) оператор и его свойства. |
20. (1 из 3) Ун-ые (ортгн-ые) матрицы и их св-ва. Переход от одного ортонормированного базиса к другому. |
|
Def:
Линейный оператор A,
действующий в унитарном U
(евклидовом E) пр-ве
называется унитарным в U
(орт. E),
если Def:
Квадратная матрица
Пусть
Свойства:
1)
Док-во:
Следствие:
2) Унитарный (ортогональный) опер-р переводит ОНБ снова в ОНБ. Док-во:
Если
3) Собств знач-яя унитарного (ортог-ного) опер-ра по модулю = 1. Доказательство (для V=U): Пусть
Al=λl,
тогда
4)
Пусть
Док-во: Аналогично док-ву свойства 5 для нормальных операторов. #
|
Def: Квадратная
матрица
Пусть
1) Определитель унитарной (ортогональной) матрицы по модулю равен 1. Доказательство (для унитарной матрицы): Т.к.
То
2)
Матрица Ae
унитарна (ортогональна) тогда и только
тогда, когда ее строки (столбцы)
нормированы и попарно ортогональны,
т.е. для строк:
Доказательство (для унитарной матрицы): Матрица
Ae
- унитарная
|
|
20. (2 из 3) Ун-ые (ортгн-ые) матрицы и их св-ва. Переход от одного ортонормированного базиса к другому. |
20. (3 из 3) Ун-ые (ортгн-ые) матрицы и их св-ва. Переход от одного ортонормированного базиса к другому. |
|
Доказательство для ортогональной матрицы аналогично 3) Произведение унитарных (ортогональных) матриц есть унитарная (ортогональная) матрица Док-во: Пусть
4)
Пусть
Док-во: Запишем
Из
единственности обратной матрицы
следует, что
Примеры ортогональных операторов. 1°
Если
Таким
образом, в одномерном евклидовом
пространстве имеются два ортогональных
преобразования:
|
2°.
Пусть
Получаем две ортогональные матрицы:
Матрица
|
|
21. (1 из 3) Спектральная теорема для нормальных операторов и нормальных матриц. |
21. (2 из 3) Спектральная теорема для нормальных операторов и нормальных матриц. |
|
Lem:
Пусть e –
собственный вектор нормального
оператора A: U
U,
Док-во:
1. Пусть
2.
Пусть
Пусть
Th : (Спектральная теорема):
1) Пусть A –
норм. оператор, действующий в унитарном
пространстве Un.
Тогда в пространстве
2) Пусть
|
Док-во: 1)
Как всякий линейный оператор, действующий
в унитарном (комплексном)
пространтсве, нормальный оператор A
имеет хотя бы одно собственное значение.
Пусть
(n-2)мерное
подпространство, инвариантное
относительно оператора A.
Теперь можно записать, что
Таким
образом, получили ОНБ
из собственных в-в
|
|
21. (3 из 3) Спектральная теорема для нормальных операторов и нормальных матриц. |
22. (1 из 2) Спектральная теорема для самосопряженных операторов и эрмитовых (симметрических) матриц. |
|
2)
Пусть
|
Th
(о связи между самосопряженным и
нормальным оператором): Оператор
A явл-ся самосопряж.
тогда и только тогда, когда: 1) A
– норм. оператор; 2) все собств. з-ия
явл-ся действ. числами, т.е.
Док-во: Необходимость Пусть
A – самосопряж. оператор,
тогда по определению
Достаточность
Пусть A – норм.
оператор и пусть все его собств.
значения
Рассмотрим
произвольные эл-ты
Th (Спектральная теорема): Пусть A
– самосопряж. оператор, действующий
в унитарном пространстве
|
|
22. (2 из 2) Спектральная теорема для самосопряженных операторов и эрмитовых (симметрических) матриц. |
23. (1 из 2) Спектральная теорема для унитарных операторов и унитарных матриц. |
1) Все собств.
2) Существует унитарная матрица
Док-во: Следует из предыдущей и спектральной теоремы для норм. операторов. # |
Th (о связи между унитарнным и нормальным оператором): Оператор
A явл-ся унитарным
тогда и только тогда, когда: 1) A
– нормальный оператор, 2) все собственные
значения по модулю равны единице,
т.е. Док-во: Необходимость Пусть
A – унитарный
оператор, тогда по определению
Достаточность. Пусть
A – норм. опер. Тогда
по спектральной теореме для норм.
операторов в унитарн. простр-ве Un
существует ОНБ – базис из собств. в-в
Если
Спектральная теорема: Пусть A – унитарный оператор, действующий в унитарном
|
|
23. (2 из 2) Спектральная теорема для унитарных операторов и унитарных матриц. |
24. (1 из 3) Приведение эрмитовой квадратичной формы к каноническому виду. |
Док-во: Следует из предыдущей теоремы и спектральной теоермы для нормальных операторов. |
Пусть
1)
Докажем, что A –
самосопряженный оператор. В самом
деле с одной стороны
2)
Пусть
Запишем
Замечание:
Если
Если
в эрмитовой полуторалинейной форме
Th 1: Пусть
|
|
24. (2 из 3) Приведение эрмитовой квадратичной формы к каноническому виду. |
24. (3 из 3) Приведение эрмитовой квадратичной формы к каноническому виду. |
|
принимает канонический вид:
Док-во: Запишем:
Разложим вектор x по данному ОНБ:
Th 2: Пусть
Док-во: Запишем:
|
принимает диагональный вид, т.к. по
замечанию в евклидовом пространстве
Вывод: Для всякой квадратичной формы в унитарном (евклидовом) пространстве существует ортогональное преобразование, приводящее квадратичную форму к каноническому виду. Замечание. С
каждой квадратичной формой
Как уже отмечалось,
в любом ОНБ в евклидовом пространстве
матрицы квадратичной формы
|
|
25. (1 из 2) Одновременное приведение пары квадратичных форм к каноническому виду. |
25. (2 из 2) Одновременное приведение пары квадратичных форм к каноническому виду. |
|
Пусть
Th 1: Пусть
Док-во:
Рассмотрим эрмитову полуторалинейную
форму
|
смысле
скалярного произведения
Th 2: Пусть
коэффициенты
Док-во: Без доказательства |
|
26. (1 из 2) Определение невырожденного линейного оператора и его свойства. |
26. (2 из 2) Определение невырожденного линейного оператора и его свойства. |
|
Как
известно (см. § 4 гл.IV)
преобразование матрицы
Def: Линейный оператор называется невырожденным, если он задается невырожденной матрицей. Замечание: Из определения следует, что любой невырожденный оператор обратим, и наоборот (см. Критерий обратимости линейного оператора, § 3 гл.IV). Свойства невырожденного оператора:
Док-во: Пусть
C=AB
, тогда в любом базисе
2. Если оператор A
является невырожденным, то обратный
ему оператор
Док-во: Т.к.
|
3.
Если оператор A
является невырожденным, то сопряженный
ему оператор
Док-во: В
произвольном ОНБ
4. Если оператор A является невырожденным, то равенство Ax=Θ возможно только при x=Θ (на это свойство мы ссылаемся § 5 гл.IV). Док-во: Пусть
|
|
27. (1 из 1) Представл невырожд лин опер-ра в виде произв самосопряженн и унитарн (ортог) операторов. |
28. (1 из 3) Многочлен от матрицы и линейного оператора. |
|
Пусть
Лемма: Линейный оператор A*A(так же как AA*) является самосопряженным при этом его собственные значения положительны. Док-во: Введем обозначение B= A*A. Запишем B*=(A*A)*=A*(A*)*= A*A (по свойствам сопряженного оператора 1-му и 2-му) следовательно, B*=B т.е. В – самосопряженный оператор. Пусть
λ - собственное значение оператора
В, х – соответствующий
собственный вектор оператора В
т.е. Bx= λx,
Пусть
λ=0, тогда
Th: Любой невырожденный линейный оператор в унитарном (евклидовом) пространстве представим в виде произведения 2-х операторов: самосопряженного и унитарного (ортогонального). Док-во: Без доказательства. Замечание: Самосопряженные и унитарные (ортогональные) операторы достаточны для описания всего множества невырожденных операторов в унитарном (евклидовом) пространстве. |
Пусть
Def:
Если
Def:
Многочленом от линейного оператора
φ называется линейный оператор
Следствие: Док-во: Следует из определения произведения 2-х операторов. # В силу
изоморфизма (взаимнооднозначного
соответствия) линейных операторов φ
и квадратных матриц А из
Def:
Говорят, что многочлен P(t)
аннулирует линейный оператор φ (матрицу
Рассм
лин пр-во квадр матриц
Это означает, что многочлен P(t) аннулирует матрицу A0. |
|
28. (2 из 3) Многочлен от матрицы и линейного оператора. |
28. (3 из 3) Многочлен от матрицы и линейного оператора. |
|
Отсюда вытекает, что существует многочлен минимальной (min) степени, аннулирующий матрицу A0. Def:
Минимальным многочленом матрицы А
( или линейного оператора
Лемма:
Пусть многочлен
Док-во: Без доказательства. Th: Всякий аннулирующий многочлен делится нацело на минимальный многочлен. Док-во:
Пусть P(t)
- аннулирующий многочлен, тогда P(A)=0.
Разделим P(t)
на
Отсюда
вытекает, что
получили
бы, что r(t)
имеет степень меньшую, чем
Следствие:
Минимальный многочлен
Док-во:
Пусть
Отмет,
что в люб баз
|
Th
(Гамельтона-Кэлли): Всякий линейный
оператор
Док-во: Рассмотрим
матрицу (A-λE).
Известно, что матрица обратная к данной
имеет вид
Здесь
Запишем:
Следствия: 1)
2) Т.к. корни минимального многочлена являются подмножеством корней характеристического многочлена (собственных значений оператора), то минимальный многочлен также разлагается на линейные множители. |
|
29. (1 из 5) Корневые векторы и корневые подпространства. |
29. (2 из 5) Корневые векторы и корневые подпространства. |
|
Def:
1: Вектор xθ
пространства V
называется корневым вектором линейного
оператора
Таким
образом, в частности всякий собственный
вектор является корневым ( Утверждения:
1) Собственный вектор –
корневой вектор высоты 1 (m=1).
2) Если справедливо
Док-во:
Пусть х- корневой вектор высоты
m, тогда
Говорят, что корневой вектор х принадлежит собств значению λ. Def:
2: Подпространство
Th 1: (о корневом подпространстве). Корневое
подпространство
Док-во:
1) Нулевой элемент
2)
Если
3)
Если
Пусть
|
Def:
3: Пусть V1
подпространство пространства V,
инвариантное относительно линейного
оператора φ, т.е.
Замечание: 1)
Если V1 и V2
- подпространства пространства V,
инвариантные относительно линейного
оператора φ и
имеет
вид:
2) Если же V1
- подпространство пространства V,
то инвариантное относительно линейного
оператора φ и других подпространств
нет, то дополняя базис
|
|
29. (3 из 5) Корневые векторы и корневые подпространства. |
29. (4 из 5) Корневые векторы и корневые подпространства. |
|
Лемма
1: Если
Док-во:
Пусть
Тогда
Пусть
Утв:Сумма
Доказательство
проведем методом математической
индукции по
1) при
2)
пусть утв справедливо для
3)
докажем справедливость утверждения
для
Т.к.
подпространство
|
Следствие:
Пусть
Док-во:
Запишем равенство
Лемма
2: Пусть
1)
При k=1:
2)
При k=2:
, а по
предположению индукции
Th
2:
Пусть
Тогда
|
|
29. (5 из 5) Корневые векторы и корневые подпространства. |
|
|
Док-во: без доказательства Следствие: Максимальная высота корневого вектора, отвечающего собственному значению λ, не превосходит кратности nλ Док-во:
Пусть
Тогда
по Лемме 2 эти векторы л.н.з. и
их всего m>nλ
штук. Это противоречит тому, что
Схемы нахождения корневых векторов. 1)
Ищем собственные значения
2) Для каждого
собственного значения λi
решаем систему уравнений
|
|
|
30. (1 из 5) Нильпотентные преобразования. Свойства нильпотентных операторов. |
30. (2 из 5) Нильпотентные преобразования. Свойства нильпотентных операторов. |
|
Def: 1: А
Линейный оператор
Наименьшее
(min) такое что:
Свойства нильпотентных преобразований: 10)Все собственные значения нильпотентного оператора A равны 0. Док-во:
Пусть х – собственный вектор
нильпотентного оператора A ,
l-показатель
нильпотентности, тогда
Следствие
1: Если A - нильпотентный
оператор, то Ker A={все
собственные векторы оператора A} Док-во: Вытек-т из опред нильпотентного оператора и свойства 1 # 20)Пусть
A - нильпотентный оператор и
Док-во:
Векторы
По лемме 2 §2 настоящей главы указанные векторы являются л.н.з. # Следствие 2: Любой
набор векторов
Док-во:
Указанный набор векторов является
л.н.з., т.к. л.н.з подсистема векторов:
Следствие 3:
Показатель нильпотентности
|
Док-во: В
противном случае если
3°)
Если l- показатель
нильпотентности, то минимальный
многочлен
Док-во:
1)
2)
Пусть r < l
(l - показатель
нильпотентности, r
– степень минимального многочлена)
и
Def:
2: Пусть A - нильпотентн опер-р
и
Линейная
оболочка z=L( порождается
элементом (вектором) x.
По свойству 20 векторы
Лемма
1: Пусть z –циклическое
подпространство, порождаемое вектором
x и dim
z = k Док-во:
Пусть
Т.к.
|
|
30. (3 из 5) Нильпотентные преобразования. Свойства нильпотентных операторов. |
30. (4 из 5) Нильпотентные преобразования. Свойства нильпотентных операторов. |
|
По
свойству
Следствие
4: Циклическое подпространство
Z инвариантно относительно
нильпотентного оператора
Док-во:
Следствие
5:
Док-во: Применить k раз следствие 4. # Вывод:
Пусть
Здесь
|
(смотри замечание 2)
Замечание 1: Пусть
A - нильпотентный оператор, с показателем
нильпотентности k.
Тогда циклическое подпространство
его
матрица в базисе
А
в базисе
рассмотрим
лин. оператор
(см. Следствие 3 раздела 3.1 § 3). Утв: 1: Показатель
нильпотентности
|
|
30. (5 из 5) Нильпотентные преобразования. Свойства нильпотентных операторов. |
31. (1 из 3) Жордановы цепочки, Нахождение начальных векторов цепочек. |
|
Док-во: Пусть минимальный многочлен имеет вид:
Будем
доказывать методом от противного.
Предположим, что
Возьмем
произвольное
Если
же
|
Пусть R Цель
: доказать что R =
Z Def:
3: Пусть
Замечание 3: Любой циклический базис состоит из собственного вектора и присоединенных к нему векторов. Обратно, Жордановой цепочка образует циклический базис. |
|
31. (2 из 3) Жордановы цепочки, Нахождение начальных векторов цепочек. |
31. (3 из 3) Жордановы цепочки, Нахождение начальных векторов цепочек. |
|
Лемма
2 Собственный вектор
e0
(0)
имеет k
присоединенных векторов (т.е. является
началом цепочки из (k+1)
вектора
Док-во: Необходимость: Пусть
Достаточность: Пусть
Нахождение начальных векторов Жордановых цепочек И |
Лемма 3: Im Док-во: Т.к. Алгоритм построения базиса (e0) в подпространстве KerA из собственных векторов: С
последними если это
потребуется добавим т.е л.н.з. векторы
из KerA которые
не лежат в ImA .
Тогда получим базис в KerA
|
|
32. (1 из 2) Разложение корневого подпространства в сумму циклических подпространств. |
32. (2 из 2) Разложение корневого подпространства в сумму циклических подпространств. |
|
К каждому собственному вектору базиса (e0) добавим присоединенные векторы тогда получим
указанная система векторов (2) образует в корн подпр-ве R базис. Отметим что каждая строка в (2) представляет жорданову цепочку. Лемма
4: Система
в-ов (2) – л.н.з. когда собств в-ры
Док-во: Доказывать будем методом математической индукции по числу векторов N в системе
Применим к данному равенству нильпотентный оператор А:
- линейная комбинация векторов (2) с числом слагаемых меньших чем (N-1) тогда в равенстве (*) остаётся
Лемма 5: Любой
вектор
|
Док-во:
Пусть
Пусть
Th 1: Подпространство R в котором задано нильпотентное преобразование А разлагается в прямую сумму подпространства циклических относительно оператора А Док-во: По
леммам 4 и 5 строится базис R
являющийся объединением циклических
базисов. Линейная оболочка каждой
цепочки из (2)-циклическое подпространство
т.е.
|
|
33. (1 из 3) Разм циклич-х прямых слагаемых. Вид матрицы нильпотент преобраз в жордановом базисе. |
33. (2 из 3) Разм циклич-х прямых слагаемых. Вид матрицы нильпотент преобраз в жордановом базисе. |
|
Разложение из теоремы 1 не единственно однако общее число слагаемых (ненулевых) в прямой сумме и их размерности находятся однозначно. Лемма 6: Если пространство R двумя способами разлагается в прямую сумму циклических подпространств то число (ненулевых) слагаемых в обоих разложениях одинаково. Док-во: Пусть
рассмотрим
=
То же
самое справедливо и для
Th 2: Пусть подпространство R двумя способами (3) разлагается в прямую сумму подпространств, циклических относительно нильпотентного оператора А. Тогда число слагаемых t какой-либо размерности k одинаково в обоих разложениях.
|
Док-во: Доказываем методом математической индукции по размерности циклических подпространств.
1) Пусть k1
– минимальная из размерностей
циклических подпространств zi
иUi,
т.е.
В левой части (p-t1) ненулевых слагаемых, согласно Лемме 6 в правой части будет столько же ненулевых слагаемых. Значит, и в правой части (3) будет равно t1 слагаемых размерности k1 (по следствию 5 из Леммы 1). 2) Пусть утверждение доказано для размерностей меньших чем (k-1) т.е. (k-1>k1).
3) Докажем справедливость утверждения
для размерности k.
Пусть левая часть (3) содержит t
подпространств с размерностью k.
На соотношение (3) подействуем
оператором Ak:
Эта операция занулит все слагаемые с
размерностями
Вид матрицы нипотентного преобразования в жордановом базисе. Def: 5: (по Леммам 4,5). Система векторов (2) – базис в корневом подпространстве R, который является объединением циклических базисов zi. Этот базис
|
|
33. (3 из 3) Разм циклич-х прямых слагаемых. Вид матрицы нильпотент преобраз в жордановом базисе. |
34. (1 из 3) Теорема Жордана. Построение жорданова базиса. |
|
называется жордановым базисом подпространства R для нильпотентного оператора A. Пусть
А – нильпотентный оператор
Выберем
в качестве базиса в подпространстве
z следующий :
Возьмем теперь в
корневом подпространстве R
базис (2). Тогда, так как
|
Пусть
Def:
6: Жордановым базисом пр-ва V
для опер-ра
Имеем:
Фиксируем
циклическое подпространство
жордановой
клетки
|
|
34. (2 из 3) Теорема Жордана. Построение жорданова базиса. |
34. (3 из 3) Теорема Жордана. Построение жорданова базиса. |
|
Таким образом, доказано следующее утверждение. Утв:
2: матрица линейного
оператора
Def: 7: матрицу вида (5), описанную в утверждении 2 называют жордановой матрицей. Нахождение матрицы линейного оператора φ в его жордановом базисе называется приведением матрицы оператора φ к жордановой нормальной форме. Th 3 (Жордана): Для
любого линейного оператора
Док-во:
возьмем жорданов базис в пространстве
V. По утверждению
2 матрица Aφ
оператора φ имеет в этом базисе
жорданову нормальную форму. Докажем
единственность J.
Для построения J
нужны корни
уравнения
с кратностями
Построение жорданова базиса и жордановой нормальной формы J линейного оператора φ, заданного матрицей A. 1)
находим корни
характеристического уравнения
|
2) Для
каждого
3)
Рассмотрим столбцы, в которых расположен
базисный минор матрицы
4) Жорданов базис получается при объединении жордановых базисов корневых подпространств. 5)
Жорданова нормальная форма J
матрицы A имеет
клеточно-диагональный вид и может
быть выписана непосредственно или
получена по формуле
Замечание:
Последовательно присоединенные
к
|
|
35. (1 из 3) Многочлены от матрицы. |
35. (2 из 3) Многочлены от матрицы. |
|
Рассмотрим
вещественную квадратную матрицу A
порядка n имеющую
все вещественные собственные значения.
Отметим еще раз (см. пар 1 гл.8),
что
Согласно теории семинарских занятий 8-9 (см выше) для любой матрицы A линейного оператора φ существует невырожденная матрица T (detT ≠ 0) такая, что J = T -1AT, отсюда можно записать, что A = TJT -1. Обозначим z+ - множество целых положительных чисел, включающее и число ноль. Лемма
1: Для любого
Док-во: Доказывать будем методом математической индукции по показателю степени S. 1)
2)
3)
Пусть утв. справедливо при
4)
Докажем справедливость утв. при
Рассмотрим жорданову нормальную форму:
|
и
Следствие:
|
|
35. (3 из 3) Многочлены от матрицы. |
36. (1 из 3) Функции от матрицы. Интерполяционный многочлен Лагранжа — Сильвестра. |
|
Вывод:
Элементы матрицы
справедливые для любого собственного
значения
Def: 1: Если для 2-х многочленов P(t) и Q(t) выполняются равенства (1), то говорят, что многочлены P(t) и Q(t) совпадают на спектре матрицы A.
|
Def: 1:
Пусть даны функция
Таким образом, функцию f(A)
от матриц. A можно
определить по следующей формуле:
здесь
Замечание 1: Выражение
для функции от матрицы
|
|
36. (2 из 3) Функции от матрицы. Интерполяционный многочлен Лагранжа — Сильвестра. |
36. (3 из 3) Функции от матрицы. Интерполяционный многочлен Лагранжа — Сильвестра. |
|
Th 1 (о существовании интерполяционного многочлена Лагранжа - Сильвестра): Пусть f(t) определена на спектре матрицы A. Тогда существует единственный
многочлен
Док-во: Без доказательства Def: 2: Многочлен
Вывод: По
определению функции от матрицы имеем
Замечание 2: Из Вывода следует, что функцию от матрицы можно находить также с помощью интерполяционного многочлена Лагранжа - Сильвестра. Th 2: Пусть
характеристический многочлен
Док-во: Без доказательства
Отметим, что в условии
теор.2 минимальный многочлен
|
Th 3: Пусть
Док-во: Без доказательства
Замечание 3: В последней формуле
выражение в фигурных скобках – сумма
первых
|




 собственные
векторы
собственные
векторы .
.

 ,
где
,
где
 - матрица перехода от (e)
к
- матрица перехода от (e)
к
 ,
отсюда
,
отсюда

 ,
где
,
где



 или
или

 ,
при этом
,
при этом
 и такое, что
и такое, что ,
получаем невырожденное преобразование
координат
,
получаем невырожденное преобразование
координат Тогда слагаемое
Тогда слагаемое
 ,
то получим, так называемый нормальный
вид квадратичной формы
,
то получим, так называемый нормальный
вид квадратичной формы

 .
.


 -пространство
всех геометрических (свободных)
векторов
-пространство
всех геометрических (свободных)
векторов



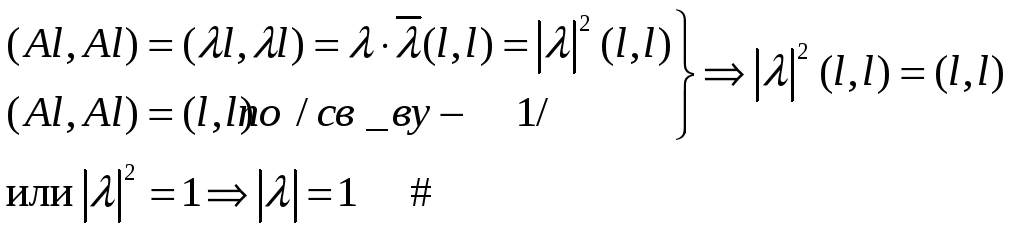
 или
или
 .
.
 причем
причем
 .
(В случае вещественных матриц
.
(В случае вещественных матриц


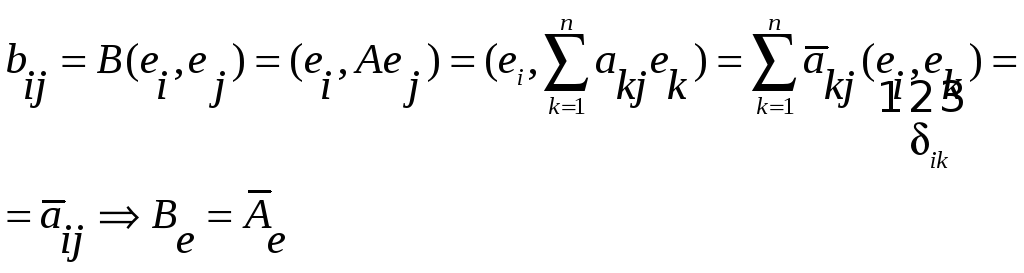

 ,
здесь
,
здесь
 ,
значит
,
значит
 ,
где
,
где
 ,
здесь *,** - ненулевые матрицы.
,
здесь *,** - ненулевые матрицы.
 z=L(
z=L(




 и
и
 =>
=>
 з
леммы2
вытекает следующее Def:
з
леммы2
вытекает следующее Def:
 троим
базис (e0) в
подпространстве KerA
из собственных векторов связанных
с (1):
троим
базис (e0) в
подпространстве KerA
из собственных векторов связанных
с (1): (2)
(2)

 (4)
- это квадратичная матрица порядка r
(4)
- это квадратичная матрица порядка r
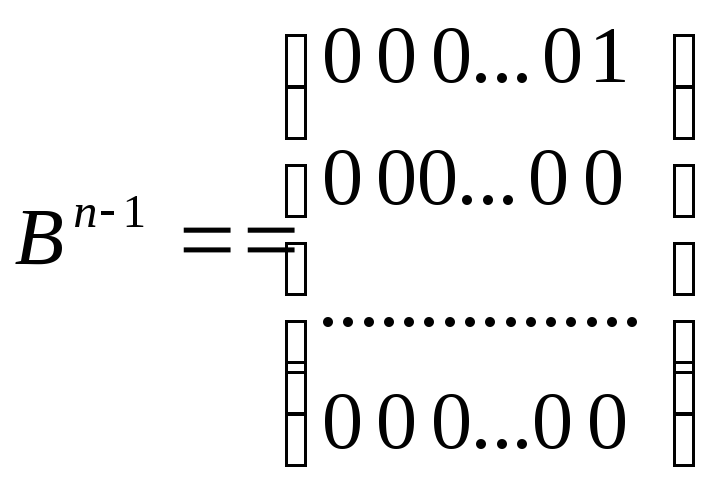
 , это квадратная матрица,
ее порядок равен dim
z
= h.
Эта матрица называется жордановой
клеткой порядка h
для собственного значения λi.
Если
, это квадратная матрица,
ее порядок равен dim
z
= h.
Эта матрица называется жордановой
клеткой порядка h
для собственного значения λi.
Если
 (5).
(5). ,
где
,
где
 ,
, ,...,
,..., ,
,
 если
если

 (1)
(1)
 ,
где
,
где
