
1 раздел вопросов к экзамену
.docxЭллипс
Определение:
геометрическое место точек т.ч. сумма
расстояний до 2 фиксированных точек
 есть величина постоянная, большая, чем
расстояние между
есть величина постоянная, большая, чем
расстояние между
 (обозначается 2а)
(обозначается 2а)
 -
фокусы эллипса; |
-
фокусы эллипса; | |
- фокусное расстояние (обознач. 2с)
|
- фокусное расстояние (обознач. 2с)
a>c;
 – фокальные радиусы;Декартова
прямоугольная с/к. (Рисунок на обороте)
– фокальные радиусы;Декартова
прямоугольная с/к. (Рисунок на обороте)
Теорема.
В декартовой с/к каноническое уравнение
эллипса имеет вид





Покажем,
что нет лишних точек.
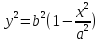 =
=
Свойства
эллипса, вытекающие из канонического
уравнения
1»
Оси Ох, Оу – оси симметрии ( )
)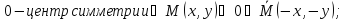 a
и
b
–
полуоси эллипса
a
и
b
–
полуоси эллипса
2»
 – точки эллипса не выходят за прямоуг.
Касательные ⊥
– точки эллипса не выходят за прямоуг.
Касательные ⊥
3»Эллипс
симметричен относительно Ох

Определение:
эксцентриситет
 ;
; ;
если
;
если
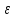 = 0 => окружность;
= 0 => окружность;
 ;Определение:
директриса эллипса
;Определение:
директриса эллипса

Теорема:
Эллипс, не являющийся окружностью есть
геометрическое место точек, для которых
отношение расстояний до фиксированной
точки F
к расстоянию до фиксированной прямой
d,
не проходящей через данную точку F,
есть величина постоянная < 1;
 (Рисунок)
(Рисунок)
Доказательство
 Пусть
Пусть



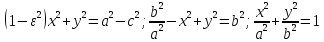
Гипербола
Определение:
гиперболой называется геометрическое
место точек для которых абсолютная
величина разности расстояний до 2-х
фиксированных точек
 есть величина большая, чем расстояние
между
есть величина большая, чем расстояние
между
 (обозначается 2а)
(обозначается 2а)
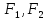 - фокусы гиперболы; |
- фокусы гиперболы; | |
- фокусное расстояние (обознач. 2с)
|
- фокусное расстояние (обознач. 2с)
a>c;
 – фокальные радиусы;
– фокальные радиусы;
Каноническая с/к – декартова прямоугольная с/к. Рис.7
Теорема:
В канонической с/к уравнение гиперболы
имеет вид

 ;
;
Свойства гиперболы, вытекающие из канонического уравнения
1»Ох,
Оу – оси симметрии, т. О – центр симметрии;
 - т. пересечения с осями; Точек пересечения
с Оу нет; Ох – вещественная ось, Оу –
мнимая.
- т. пересечения с осями; Точек пересечения
с Оу нет; Ох – вещественная ось, Оу –
мнимая.
2» ;
;
 ;
Рис.8
;
Рис.8
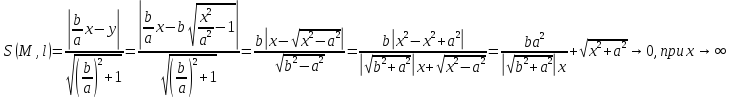 Определение
Определение
 ;Рис.9
;Рис.9
Гипербола
есть геометрическое место точек, для
которых отношение расстояния до точки
 к расстоянию до данной прямой
к расстоянию до данной прямой
 ,
не проходящей через
,
не проходящей через
 ,
есть величина постоянная
,
есть величина постоянная
 .
.
Парабола
Геометрическое
место точек, для которых расстояние до
некоторой фиксированной т. равно расстоянию до фиксированной
прямой
равно расстоянию до фиксированной
прямой
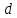 ,
не проходящей через т.
,
не проходящей через т.
 ;
;
 ;F
- фокус параболы; d
– директриса параболы; p
– расстояние от F
до d(фокальный
параметр параболы)
;F
- фокус параболы; d
– директриса параболы; p
– расстояние от F
до d(фокальный
параметр параболы)
Каноническая
с/к. Рис.10; Теорема: В канонической с/к
каноническое уравнение параболы имеет
вид
 ;
;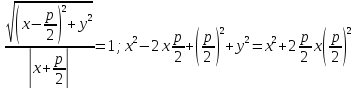 ;
;
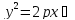 Рис.11
Рис.11
Свойства
1»Ох
– ось симметрии; т.О – вершина параболы
т.О – вершина параболы
2»
Полярные уравнения эллипса, гиперболы и параболы
Рис.1,Рис.2,Рис.3,Рис.4,Рис.5
 ;Общее
уравнение
;Общее
уравнение
 ;
; Рис.6
Рис.6
Общее уравнение линий 2-го порядка. Преобразование коэффициентов уравнения линии 2-го порядка при параллельном переносе и повороте декартовой с/к
Преобразование
коэффициентов линии 2-го порядка при
переходе к новой с/к

1»Параллельный перенос


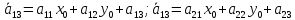

2»Поворот
на

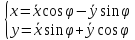

 ;
;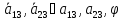

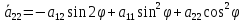
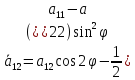
Инварианты уравнения линии 2-го порядка. Понятие типа линии 2-го порядка.
Определение:
инвариантом уравнения линии 2-го порядка
относительно преобразования декартовой
с/к называется такая ,
зависящая от коэффициентов уравнения
линии 2-го порядка, значение которой не
меняется при переходе к новой декартовой
с/к;
,
зависящая от коэффициентов уравнения
линии 2-го порядка, значение которой не
меняется при переходе к новой декартовой
с/к;
Теорема: Величины – инварианты для линий 2-го порядка
 ;
; ;
;
Доказательство
для
 -
очевидно, т.к.
-
очевидно, т.к.
 не меняется
не меняется


 =
=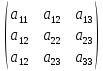
Доказательство для поворота
 ;
; ;
; – не зависит от
– не зависит от

 – эллиптический
тип;
– эллиптический
тип;
 – параболический тип;
– параболический тип; -
гиперболический тип
-
гиперболический тип
Упрощение уравнения линий 2-го порядка.
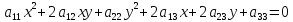
1»Параллельный перенос
 ⇔
⇔ -
уравнение центра
-
уравнение центра




Если
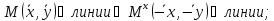
 -
центр симметрии; центральные линии.
-
центр симметрии; центральные линии.
2»Поворот

 ⇒
⇒

Упрощение уравнения центральной линии 2-го порядка. Классификация центральных линий.
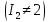 ;
;
 - центр
- центр

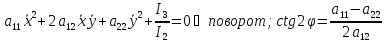
 ;
Теорема: пусть уравнение эллиптического
типа
;
Теорема: пусть уравнение эллиптического
типа и уравнение нормировано т.ч.
и уравнение нормировано т.ч.
 ,
тогда при
,
тогда при
 - уравнение эллипса,
- уравнение эллипса, – точка,
– точка,
 – уравнению не удовлетворяет ни одна
точка – мнимый эллипс.
– уравнению не удовлетворяет ни одна
точка – мнимый эллипс.
Упрощение линий параболического типа. Классификация линий параболического типа.

 линия
параболического типа. Для
линия
параболического типа. Для
 докажем.
Пусть
докажем.
Пусть
 ,
,
 ;
;
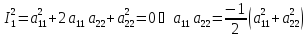 ;
;
 - линия 2-го порядка(противоречие)
- линия 2-го порядка(противоречие)

1» Преобразование поворота(стандартное упрощение)
А)Если
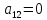 ничего делать не надо
ничего делать не надо
Б) ⇒поворот
⇒поворот
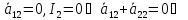 один из них 0
один из них 0

 ;
;

 ;
;

Уравнение
параболического типа;
 – представляет собой параболу, при
– представляет собой параболу, при
 – пара параллельных действительных
прямых(которые могут совпадать) или
пару мнимых параллельных прямых.
Доказательство:
– пара параллельных действительных
прямых(которые могут совпадать) или
пару мнимых параллельных прямых.
Доказательство:
1»

 или
или
 ;
; =0;
=0;
2»
 ;
;
A» – пара
слившихся прямых
– пара
слившихся прямых
Б» – пара
параллельных прямых
– пара
параллельных прямых
В» -
пара мнимых параллельных прямых
-
пара мнимых параллельных прямых
Понятие поверхности 2-го порядка. Центр поверхности 2-го порядка. Понятие центральной поверхности 2-го порядка.

1»Параллельный перенос

2»Стандартные
упрощения

Классификация центральных поверхностей 2-го порядка
 Параллельный
перенос + стандартное упрощение
Параллельный
перенос + стандартное упрощение

1) – одного знака
– одного знака
A» (>0)
(>0) – мнимый эллипсоид
– мнимый эллипсоид
Б» противоположен
по знаку
противоположен
по знаку
 эллипсоид
эллипсоид
В»

 -
вырожденный эллипсоид
-
вырожденный эллипсоид
2» –
одного знака,
–
одного знака,
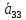 – противоположного.
– противоположного.
 – двухполостной гиперболоид
– двухполостной гиперболоид
3»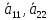 – одного знака,
– одного знака,
 противоположного
противоположного
 -
однополостной гиперболоид
-
однополостной гиперболоид
4» – одного знака,
– одного знака,
 противоположного
противоположного конус 2-го порядка
конус 2-го порядка
Классификация нецентральных поверхностей 2-го порядка
 – гиперболический
параболоид;
– гиперболический
параболоид;
 – стандартное упрощение;
– стандартное упрощение;
 один из ненулевых обращается в 0; 1»
один из ненулевых обращается в 0; 1»

А» ;
;
 ;
; – пара пересек. плоскостей,
– пара пересек. плоскостей,
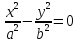 – пара мнимых пересек. плоскостей
– пара мнимых пересек. плоскостей
Б» ;
;
 - эллиптический цилиндр;
- эллиптический цилиндр; – гиперболический цилиндр
– гиперболический цилиндр
В» – параболоид;
– параболоид; – эллиптический гиперболоид
– эллиптический гиперболоид
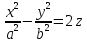 – гиперболический
параболоид
– гиперболический
параболоид
2)из
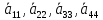 ,
,

