Парабола
В школьном курсе
математики достаточно подробно изучалась
парабола, которая, по определению,
являлась графиком квадратного трехчлена.
Здесь мы дадим другое (геометрическое)
определение параболы.
Определение:
Параболой
называется множество точек плоскости,
равноудаленных от данной точки,
называемой фокусом,
и данной прямой, называемой директрисой
параболы.
Пусть расстояние
между фокусом
и
директрисой
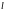 параболы
равно
параболы
равно
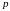 .
.
Тогда каноническое
уравнение параболы имеет вид:
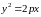 ,
,
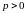

Число
называется параметром параболы. Начало
координат
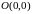 -
ее вершина, а ось
- ось симметрии. Фокусом параболы служит
точка
-
ее вершина, а ось
- ось симметрии. Фокусом параболы служит
точка
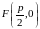 ,
а директриса имеет уравнение
,
а директриса имеет уравнение
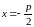 .
.
Уравнение
называется
каноническим
уравнением параболы. Парабола, симметричная
относительно оси
,
имеет уравнение
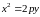 .
.
Уравнения могут
иметь вид
 ,
,
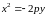 .
Как расположены они в этом случае?
.
Как расположены они в этом случае?
Пример:
Постройте параболу
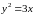 .
Найдите ее фокус и директрису.
.
Найдите ее фокус и директрису.
Решение:
Уравнение
является каноническим уравнением
параболы,
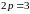 ,
,
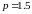 .
Осью параболы служит ось
,
вершина находится в начале координат,
ветви параболы направлены вдоль оси
.
Для построения найдем несколько точек
параболы. Для этого придаем значения
переменному
.
Осью параболы служит ось
,
вершина находится в начале координат,
ветви параболы направлены вдоль оси
.
Для построения найдем несколько точек
параболы. Для этого придаем значения
переменному
 и
находим значения
и
находим значения
 .
Возьмем точки
.
Возьмем точки
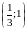 ,
,
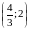 ,
,
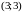 .
Учитывая симметрию относительно оси
,
рисуем кривую (рис.)
.
Учитывая симметрию относительно оси
,
рисуем кривую (рис.)

Рис. Парабола,
заданная уравнением
Фокус
лежит
на оси
на
расстоянии
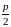 от вершины, то есть имеет координаты
от вершины, то есть имеет координаты
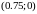 .
Директриса
.
Директриса
 имеет
уравнение
,
то есть
имеет
уравнение
,
то есть
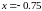 .
.
9


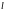 параболы
равно
параболы
равно
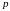 .
.
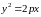 ,
,
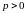

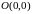 -
ее вершина, а ось
- ось симметрии. Фокусом параболы служит
точка
-
ее вершина, а ось
- ось симметрии. Фокусом параболы служит
точка
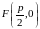 ,
а директриса имеет уравнение
,
а директриса имеет уравнение
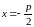 .
.
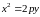 .
. ,
,
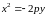 .
Как расположены они в этом случае?
.
Как расположены они в этом случае?
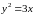 .
Найдите ее фокус и директрису.
.
Найдите ее фокус и директрису.
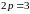 ,
,
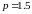 .
Осью параболы служит ось
,
вершина находится в начале координат,
ветви параболы направлены вдоль оси
.
Для построения найдем несколько точек
параболы. Для этого придаем значения
переменному
.
Осью параболы служит ось
,
вершина находится в начале координат,
ветви параболы направлены вдоль оси
.
Для построения найдем несколько точек
параболы. Для этого придаем значения
переменному
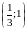 ,
,
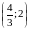 ,
,
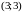 .
Учитывая симметрию относительно оси
,
рисуем кривую (рис.)
.
Учитывая симметрию относительно оси
,
рисуем кривую (рис.)
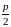 от вершины, то есть имеет координаты
от вершины, то есть имеет координаты
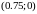 .
Директриса
.
Директриса
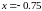 .
.