Кривые второго порядка

 Определение:  Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка:

Окружность

Начнем с определения окружности, известного из школьного курса математики.

       

Определение:  Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.     

Окружность радиуса с центром в точке имеет уравнение:

 

Пример: Нарисуйте кривую

Решение:

Итак, центр окружности - , радиус равен 2

Эллипс

  Определение:  Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.  Обозначим 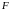  и 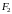- фокусы эллипса.  Начало декартовой системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось - перпендикулярно к этому отрезку.  

Пусть сумма расстояний от точки эллипса до фокусов равна , а расстояние между фокусами - . Тогда в выбранной системе координат эллипс имеет уравнение  

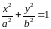
где

        Определение:   Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии - центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины - большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины - малой полуосью.

Величина

называется эксцентриситетом эллипса, (характеризует степень сжатости эллипса к оси ).        

Если эллипс задан каноническими уравнениями, то его вершины имеют координаты , , , , большая полуось равна , малая полуось равна  . Величина , являющаяся половиной расстояния между фокусами, определяется из формулы для величины , а именно, .

Но кривую, определяемую уравнением , мы можем рассмотреть и в случае , . Уравнение в этом случае после умножения на примет вид . Это - уравнение окружности радиуса с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда , , 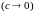или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.  

Эксцентриситет эллипса характеризует степень вытянутости эллипса, как уже говорилось. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса .

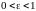Пример: Постройте кривую . Найдите фокусы и эксцентриситет.

Решение: Разделим обе части уравнения на 36. Получаем уравнение

Это - каноническое уравнение эллипса, , . Делаем чертеж

Рис. Эллипс, заданный уравнением

находим , . Фокусы -- , , эксцентриситет -         

Гипербола

Из школьного курса математики известно, что кривая, задаваемая уравнением , где  – некоторое число, называется гиперболой. Однако это  только частный случай гиперболы (равносторонняя гипербола).

       

 Определение: Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.         

Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.

        Пусть расстояние между фокусами и гиперболы равно ,т.е , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна . Тогда гипербола в выбранной выше системе координат имеет уравнение:

; где

Прямые являются асимптотами гиперболы.

Для построения гиперболы необходимо построить осевой прямоугольник, со сторонами и . Центр этого прямоугольника расположен в начале координат. Далее необходимо провести диагонали этого прямоугольника, которые будут являться асимптотами для гиперболы .Вершины гиперболы будут лежать в точках и - .

    Точки пересечения гиперболы, заданной каноническим уравнением  с осью называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками и называется мнимой осью. Числа и называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром.

Величина

Отношение - называется эксцентриситетом гиперболы.         

        Для гиперболы справедливо , то есть у гиперболы . Эксцентриситет характеризует угол между асимптотами, чем ближе к 1, тем меньше этот угол.         

      

  Замечание: В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами и может быть произвольным. В частности, при мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид , если взять , а оси и направить по биссектрисам четвертого и первого координатных углов, то (см. рис.)

Рис. Равносторонняя гипербола

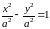
 Пример: Постройте гиперболу , найдите ее фокусы и эксцентриситет.

Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение

, . Проводим асимптоты и строим гиперболу (рис. ).

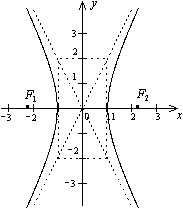
Рис.Гипербола

Из формул получаем . Тогда фокусы - , , .