28) Биномиальный коэффициент

Материал из Википедии — свободной энциклопедии

Перейти к: навигация,поиск

В математике биномиальные коэффициенты — это коэффициенты в разложениибинома Ньютонапо степенямx. Коэффициент при обозначается(иногда) и читается «биномиальный коэффициент изn по k» (или «це из n по k»):

В комбинаторикебиномиальный коэффициентинтерпретируется как количествосочетанийизn по k, то есть количество всех подмножеств (выборок) размераk в n-элементном множестве.

Биномиальные коэффициенты часто возникают в задачах комбинаторикиитеории вероятностей. Обобщением биномиальных коэффициентов являютсямультиномиальные коэффициенты.

Явные формулы

Значение биномиального коэффициента определено для всех целых чиселn и k. Явные формулы для вычисления биномиальных коэффициентов:

для

для или

для

где обозначаетфакториалчислаm.

Треугольник Паскаля

Тождество

позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

Треугольная таблица, предложенная Паскалемв «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье,О. Хайямуи др.).

Строки в треугольнике Паскаля в пределе стремятся к функции нормального распределения.

Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника и повернув квадрат на любой из четырёх углов, то детерминант этих четырёх матриц по модулю равен 1 при любом N. Если поставить уголом из 1 в верхний левый угол, то детерминант матрицы будет равен 1.

В матрице 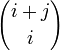числа на диагонали i+j = const повторяют числа строк треугольника Паскаля. (i,j = 0...∞)

Матрицу где i, j = 0…p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Элементы такой матрицы

где i,j = 0...p Далее обратная матрица к U

таким образом можно разложить обратную матрицу к в произведение двух строго диагональных матриц и дать явное выражение для обратных элементов. Первая верхнетреугольная, а вторая получается из первой путем транспонирования.

i,j,m,n = 0...p, если выражение в кваратных скобках ложно, то элемент суммы равен 0. Элементы обратной матрицы меняются при изменение её размера и в отличие от матрицы 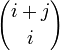недостаточно приписать новую строку и столбец.

Свойства Производящие функции

Для фиксированного значения n производящей функциейпоследовательности биномиальных коэффициентовявляется:

Для фиксированного значения k производящей функцией последовательности биномиальных коэффициентов является:

Двумерной производящей функцией биномиальных коэффициентов является:

Делимость

Из теоремы Люкаследует, что:

• нечётен вдвоичной записичислаk единицы не стоят в тех разрядах, где в числе n стоят нули.

• некратен простому p вp-ичной записи числа k все разряды не превосходят соответствующих разрядов числа n.

• В последовательности биномиальных коэффициентов :

  • все числа не кратны заданному простому p 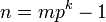, где натуральное числоm < p;

  • все числа, кроме первого и последнего, кратны заданному простому p ;

  • количество нечётных чисел равно степени двойки (степень двойки равна количеству единиц в двоичной записи числа n);

  • не может быть поровну чётных и нечётных чисел;

  • количество не кратных простому p чисел равно , где числа— разрядыp-ичной записи числа n; а число — её длина.