4.2 Расклинивающее давление

При сближении частиц дисперсной фазы толщина пленки (прослойка среды) между частицами сильно уменьшается. Тонкий слой жидкости приобретает свойства, отличные от свойств жидкости в объеме. Если толщина пленки h меньше двух толщин поверхностных слоев ( ), поверхностные слои начинают перекрываться, что приводит к появлению в системе дополнительных сил - расклинивающего давления (рис.4.2). Расклинивающим давлением П(h) называется разность между давлением р в прослойке жидкости, разделяющей частицы, и давлением р_о в объемной

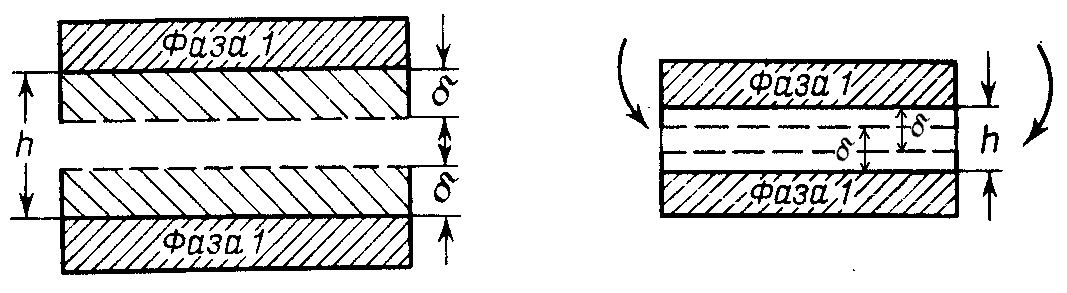
Рис. 4.2. Схема, поясняющая возникновение расклинивающего давления

жидкой фазе, находящейся в термодинамическом равновесии с жидкостью в прослойке:

(4.6)

Его можно рассматривать как давление, которое надо приложить к пленке, чтобы сохранить ее равновесную толщину. Расклинивающее давление - суммарный параметр, учитывающий молекулярные силы притяжения, и силы отталкивания различной природы, соответствующие факторам устойчивости.

В соответствии с этим расклинивающее давление может быть положительным, вызывающим утолщение пленки и противодействующим сближению частиц, и отрицательным, утончающим пленку и способствующим коагуляции.

Различают следующие составляющие расклинивающего давления: молекулярную, электростатическую, структурную, адсорбционную и стерическую.

Молекулярная составляющая расклинивающего давления обусловлена ван-дер-ваальсовым взаимодействием частиц дисперсной фазы.

Электростатическая составляющая возникает в тех случаях, когда на поверхности частиц имеется двойной электрический слой. Она обусловлена электростатическим взаимодействием частиц и проявляется при их сближении на расстояние порядка удвоенной толщины двойного электрического слоя.

Структурную составляющую расклинивающего давления связывают с сольватацией поверхности частиц, т.е. с образованием поверхностных слоев жидкости с особой структурой, отличной от структуры той же жидкости в объеме.

Адсорбционной составляющей расклинивающего давления принято называть силу притяжения или отталкивания, возникающую при перекрытии диффузных адсорбционных слоев из молекул среды.

Стерической составляющей расклинивающего давления объясняется стабилизирующее действие ВМС и неионогенных ПАВ.

Удовлетворительному расчету поддаются только молекулярная и электростатическая составляющие расклинивающего давления, именно эти составляющие учитывает теория устойчивости и коагуляции ДЛФО

4.3 Основные положения теории длфо

В основе современной теории устойчивости дисперсных систем, развитой в работах Дерягина, Ландау, Фервея и Овербека (теория ДЛФО), лежит представление о том, что между поверхностями частиц действуют межмолекулярные (ван-дер-ваальсовы) силы притяжения и силы отталкивания электростатической природы, и поведение системы зависит от соотношения этих сил. Эта теория удовлетворительно описывает закономерности поведения лиофобных дисперсных систем.

Для количественного описания положений теории ДЛФО рассматривается взаимодействие крупных частиц. В этом случае оно аналогично взаимодействию между двумя плоскими параллельными пластинами. Общая энергия взаимодействия U между двумя частицами, приходящаяся на единицу их площади, зависит от расстояния h между ними и равна

U(h) = Ue (h)+Um (h)

(4.7)

где U_e(h) и U_m(h) - энергия электростатического отталкивания и молекулярного притяжения соответственно.

Межмолекулярные силы действуют как между отдельными молекулами, так и между частицами, состоящими из большого числа молекул. Согласно приближенным расчетам, проведенным де Буром и Гамакером, энергия притяжения обратно пропорциональна квадрату расстояния между частицами:

,

(4.8)

где A* - постоянная, учитывающая константы Гамакера для дисперсной фазы и дисперсионной среды и их взаимодействие.

Это значит, что силы взаимодействия частиц действуют на значительно больших расстояниях, чем силы взаимодействия двух молекул, следовательно, энергия взаимодействия двух частиц убывает значительно медленней.

Электростатическая теория устойчивости дисперсных систем применима к тем системам, устойчивость которых обеспечивается только электростатическим фактором. Электростатические силы отталкивания обусловлены наличием на поверхности частиц двойного электрического слоя. Так как суммарные заряды обеих обкладок двойного электрического слоя равны и противоположны по знаку, то их действие на любой заряд за пределами двойного слоя будет равно нулю. Действие внутренней обкладки компенсируется действием наружной. Следовательно, при сближении двух таких поверхностей взаимодействие начнется только после того, как произойдет наложение (перекрытие) их двойных слоев (рис.4.1). При этом частицы попадают в поле действия одноименных зарядов поверхности и испытывают силы отталкивания. Таким образом, толщина двойного электрического слоя дает представление о радиусе действия сил электростатического отталкивания.

Для вывода зависимости энергии отталкивания от расстояния были привлечены положения теории Гуи-Чепмена, уравнения Пуассона и Пуассона-Больцмана. Конечные выражения имеют вид:

для области низких потенциалов

(4.9)

при больших значениях потенциалов

(4.10)

Из уравнений (4.9) и (4.10) следует, что энергия отталкивания частиц возрастает с уменьшением расстояния h между ними по экспоненциальному закону.

Сложением U_e и U_m получают общую энергию взаимодействия между двумя пластинами (частицами) для области малых и высоких потенциалов соответственно:

	(4.11)
	(4.12)

В соответствии с (4.11) и (4.12) результат столкновения частиц зависит от соотношения между силами притяжения и отталкивания, т.е. от знака и значения суммарной потенциальной энергии взаимодействия частиц. .

Для оценки агрегативной устойчивости дисперсных систем удобно пользоваться потенциальными кривыми взаимодействия. Потенциальные кривые взаимодействия частиц, т.е. кривые зависимости суммарной энергии взаимодействия частиц от расстояния между их поверхностями - U(h), получены геометрическим сложением ординат U_е(h) и U_m(h) (рис4.3). Положительная энергия отталкивания U_е(h) с увеличением расстояния уменьшается по экспоненциальному закону, а отрицательная энергия притяжения U_m(h) обратно пропорциональна квадрату расстояния. Поэтому на малых расстояниях и на больших расстояниях (экспонента убывает значительно быстрее, чем степенная функция) между частицами преобладает энергия притяжения (потенциальная кривая суммарного взаимодействия лежит в отрицательной области координат).

Область малых расстояний характеризуется первичным потенциальным минимумом U_min.I, область больших расстояний - вторичным потенциальным минимумом U_min.II.

Р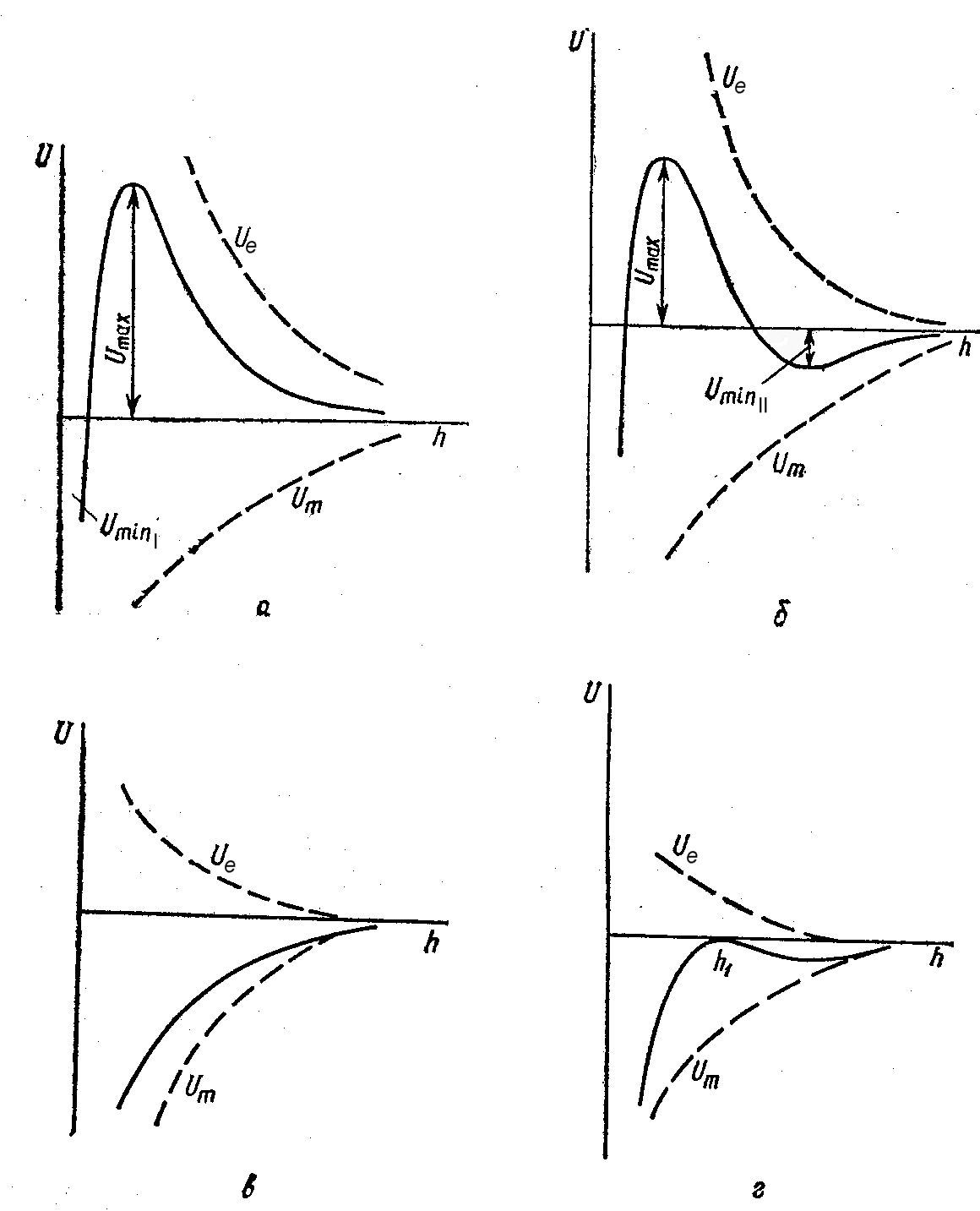 ис. 4.3. Потенциальные кривые взаимодействия частиц в дисперсных системах с различной степенью устойчивости.

Если частицы попадают в область первичного потенциального минимума, то они слипаются, а во вторичном минимуме U_min.II частицы притягиваются и фиксируются друг относительно друга через прослойку дисперсионной среды.

На средних расстояниях элекростатические силы отталкивания больше молекулярных сил притяжения и U(h)>0. Максимум энергии суммарного взаимодействия (U_max), соответствующий средним расстояниям между частицами, характеризует потенциальный барьер, препятствующий слипанию частиц.

Из множества потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем, можно выделить три наиболее характерные зависимости потенциальной энергии взаимодействия от расстояния между частицами (рис.). Кривая а 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии k_БТ. Чтобы произошла коагуляция необходимо преодолеть потенциальный барьер. Барьер не будет преодолен, если кинетическая энергия самих частиц, равная в среднем k_БT, будет меньше U_max. Это агрегативно устойчивая система.

На кривой б 2 имеется достаточно высокий потенциальный барьер и вторичный потенциальный минимум. В системе, отвечающей такому состоянию, происходит так называемая частичная коагуляция - фиксация частиц друг относительно друга на расстояниях, соответствующих вторичному минимуму, причем частицы не имеют непосредственного контакта и разделены прослойками среды. Очевидно, что такое состояние отвечает обратимости коагуляции. Обратный процесс - пептизация - возможен после устранения вторичного минимума или уменьшения его до значения ниже k_БT.

Кривая в 1 соответствует такому состоянию системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания. При таком состоянии для дисперсной системы характерна быстрая коагуляция: любое столкновение между частицами заканчивается их слипанием

Электростатические силы отталкивания между частицами обусловлены возникновением двойного электрического слоя и величина электростатического барьера определяется, главным образом, электрическим потенциалом и толщиной двойного электрического слоя. Следовательно, соотношение между силами притяжения и отталкивания можно регулировать изменением концентрации электролита в дисперсионной среде.