1 Дв интеграл, определение, свойства и вычисление
2 Дв интеграл в полярных координатах
3 Интеграл Пуассона
4 Тр интеграл, определение, свойства и вычисление
5 Тр интеграл в цилиндрических координатах
6 Тр интеграл в сферических координатах
7 Криволинейные интегралы 1-го рода
8 Криволинейные интегралы 2-го рода
9 Формула Грина, вычисление площади
10 Независимость интеграла 2-го типа от формы кривой на плоскости
11 Поверхностный интеграл 1 рода
12 Поверхностный интеграл 2 рода
13 Формула Стокса, ротор векторного поля
14 Формула Гаусса-Остроградского, дивергенция векторного поля
15 Сходимость и расходимость числовых рядов,
необходимый признак сходимости, принцип Коши
16 Положительные ряды, признаки сравнения
17 Признак Даламбера
18 Радикальный признак Коши
19 Интегральный признак Коши
20 Абсолютная и условная сходимость, признак Лейбница
21 Степенные ряды и лемма Абеля
22 Радиус сходимости и свойства суммы степенного ряда
23 Ряды Тейлора и Маклорена, теорема о разложении
24 Определение ряда Фурье и признак сходимости Дирихле
25 Ряды Фурье четных и нечетных функций
26 Разложение только по sin или только по cos
27 Разложение на промежутке [−l, l ]
28 Закон Фурье и уравнение теплопроводности
Двойные интегралы
Основные понятия и определения. Рассмотрим функцию f опред и огранич на прямоуг A R2 , пусть τ разбиение A на n прямоуг, их площади
и
диаметры =
,
в
прямоуг выберем т
и образуем сумму Римана:
.
Введем
ранг разбиения
и определим предел сумм.
,
если
:
как только
независимо
от
Дв
интегралом наз число
,
если предел существует, при этом f
наз интегрируемой функцией по множеству
A.
Нам понадобится понятие нулевой площади: множество E R2 имеет нулевую площадь, если его можно покрыть конечным числом прямоуг, для которых сумма площадей сколь угодно мала. Пр.: график непр функции на отрезке, кусочногл кривая имеют нулевую площадь.
Дост признак инт. Если E A имеет нулевую площадь, а f непр в A – E, то f инт по A.
Пусть
множ D
R2
ограничено кусочногл кривой (граница
имеет нулевую пл), а f
непр на D,
тогда
прямоуг A
D,
определим функцию
:
и
,
инт по A,
т.к. ее точки разрыва имеют нулевую пл,
положим по опред.
,
все!
Пр.
,
по опред.
Зам: если f ≥ 0, то инт суммы = объему ступенчатых тел, предел таких сумм, если он наз. объемом подграфика f .
Пример
объем 1/2 шара радиуса 1.
Свойства
1
Линейность.
2
Аддитивность. Пусть множество D
разделено кусочногл кривой на 2 части
,
тогда
3
Монотонность.
,
,
4
Т. о ср. знач. Пусть f
непр на D
тогда
,
наз. ср.
знач. f
на D.
Пр.
,
ср. знач. высоты полусферы=2/3, объем
полушара делим на пл. основания (круга),
радиус полусферы=1.
Вычисление
1
Повторные интегралы это конструкции
вида
Пр.
2
Правильные допуст множ. Пусть
непр на [a,b],
и D
часть плоскости ограниченная этими
графиками. D
наз прав вдоль OY.
Пр.
− верхний полукруг, прав вдоль OY:
,
и вдоль OX:
3
Т. Фубини. Пусть D
прав. вдоль OY,
опред.
,
а f
непр в D,
тогда
Пр.
Приложение
1
Объем и масса. Если функция f
неотрицательна и непр на множ D,
то ее подграфик Ω наз. цилиндр телом и
его объем
,
если f
плот, то инт. дает массу
пластины, если f=1,
то инт. равен площади
.
2 Статические моменты и центр масс плоской фигуры
,
.
Пр. центр масс полукруга.
3
Моменты инерции плоской фигуры
.
4
Площадь графика гл. функции
.
Замена переменных в двойном интеграле
1 Схема замены. Пусть G и G' две плоские области, G отнесена к (x,y), а G' к (u,v), и они связаны соотношениями
,
которые
опред. отображение Φ из G'
в G:
соответствует
пара
.
Будем считать, что Φ удовлетворяет
следующим условиям:
1) Φ вз-одн: G' G: разным парам в G' отвечают разные пары в G;
2)
Φ гл.:
непр
диф,
-
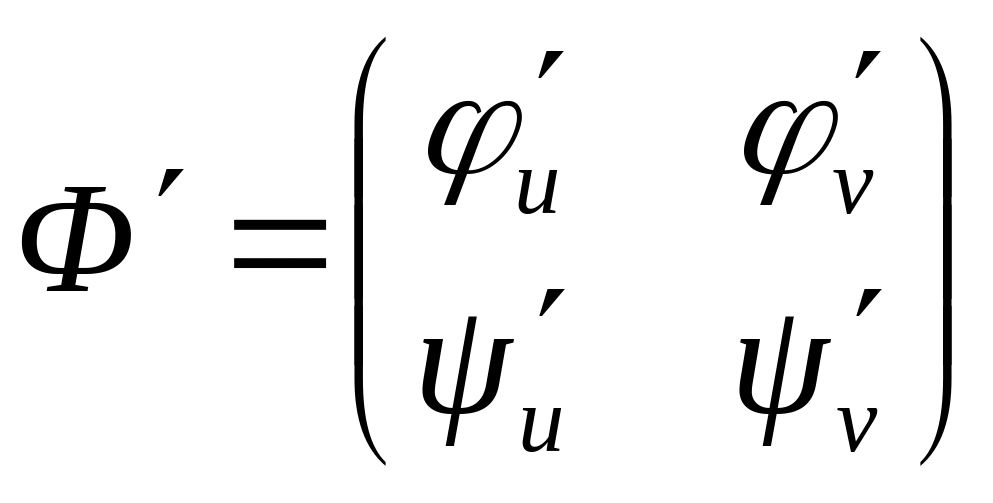матр Якоби,
- якобиан;
3)
.
Формула замены в двойном интеграле.
Пусть
1)
−допуст
множ., 2) f
непр в D,
3)
и Φ(D')=D
Пр.
.
2 Двойной интеграл в полярных координатах
Φ:
,
,
,
,
Пр.
- часть кольца,
Интеграл
Пуассона
.
Докажем
, что
1)
Инт. сх. по признаку сравнения:
достаточно больших x;
2) Пусть a>0, берем квадрат D(a)= [0,a]×[0,a] и преобразуем инт.
;
3)
Рассмотрим части кругов
в первой четверти, имеем
и
;
4)
Выч. крайние инт.
=
=
,
5) Переходим к пределу в неравенстве
,
, все!
Тройные интегралы
Определения.
Пусть f
опред. и огранич в паралл A
, τ -разбиение A
на n
паралл, их объемы и диаметры =
,
в
паралл. выберем т
и образуем сумму
.
Введем ранг τ:
и определим предел интегральных сумм:
,
если
как только
независимо от
Тройным
интегралом от f
по A
наз. число
,
если предел существует, при этом f
наз интегрируемой функцией по A.
Далее,
множество
имеет
нулевой объем, если его можно покрыть
конечным числом параллелепипедов, сумма
объемов которых сколь угодно мала.
Пр., график непр. функции двух переменных на ограниченном и замкнутом множестве, гладкая поверхность имеют нулевой объем.
Признак
инт.: если
имеет
нулевой объем, а f
непр. в
,
то f
инт. по A.
Далее,
множ.
наз. допуст. если оно ограничено, замкнуто
и его граница имеет нулевой объем.
Определим тр. интеграл по такому множ.
Пусть f
непр. на допуст. множ. Ω , тогда
параллелепипед A
Ω , определим
:
,
,
она инт. по A
, ее точки разрыва имеют нулевой объем,
положим по опред.
.
Пр.
;
-объем
Ω
по опред.
Свойства
1
Линейность
2
Аддитивность. Пусть Ω
разделена поверхностью на 2 части
, тогда
3
Монотонность. 1)
, 2)
,
3)
4
Т. о среднем значении. Пусть f
непр. на допуст. множ Ω , тогда
,
наз. ср. знач. f
на Ω.
Вычисление
1
Повторные интегралы. Это конструкции
вида
или
Пр.
1)
2)
,
2
Прав допуст множ. Пусть функции
непрерывны на
замкнутом и ограниченном множестве D
с кусочно-гладкой границей и
на D.
Множ
наз. правильным вдоль OZ
.
3
Т. Фубини о сведении тройного интеграла
к повторному. Пусть множ Ω прав вдоль
OZ,
опред функциями
,
а f
непр в Ω, тогда
.
Пр.
Приведем
еще одну конструкцию повторного
интеграла, к которому сводится тройной
интеграл. Пусть Ω занимает вдоль Z
отрезок [a,b]
и сечения D(z)
– допуст. множ, тогда
,
если
внутренний двойной инт. по сечениям.
Приложение
1)
Масса тела
,
объем
2) Ст. моменты и ц. м. трехмерной фигуры
3)
Моменты инерции трехмерной фигуры
относительно осей координат
Замена переменных в тройном интеграле
1 Схема замены. Пусть G и G’ две области в R3, G отнесена к
координатам
(x,y,z),
а G'
к (u,v,w).
Предположим, что G
и G'
связаны соотношениями, запишем их в
виде
,
,
,
, они опред.
отображение Φ:G'
G
. Будем считать, что Φ удовлетворяет
следующим условиям:
1)
Φ
вз-одн.; 2) Φ гладкое, а значит определена
матр Якоби
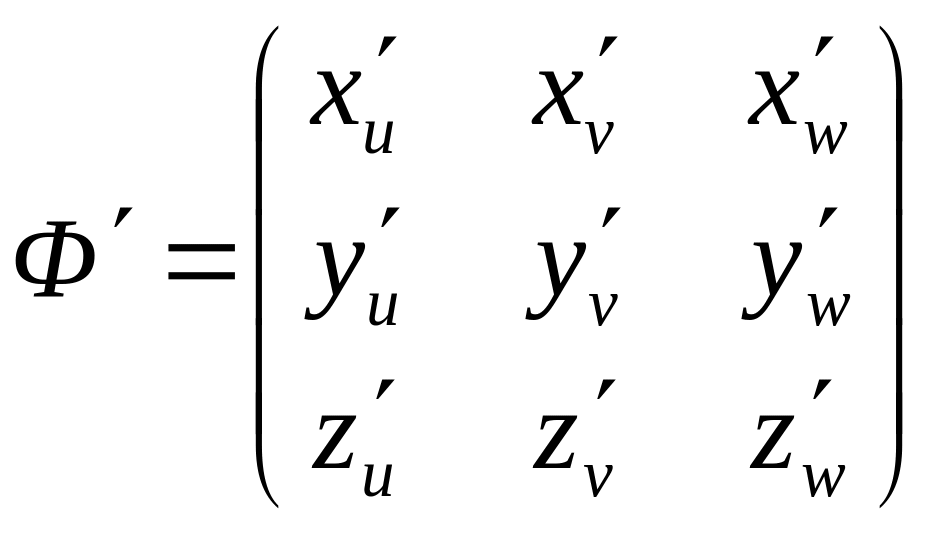и якобиан
;
3) .
Формула замены переменных в тройном интеграле.
Пусть
1)
допуст. множ, 2) f
непр в Ω,
3)
и
